Berkson-Gage寿命表与无校正寿命表
作者：赵国龙
单位：河南医科大学(450052)
关键词：终检；有效性；寿命表；自相容性；生存率；无偏性
中国卫生统计990503 【提 要】 目的 本文提出无校正寿命表，并同Berkson-Gage寿命表作以比较。方法 其构造，除在计算条件死亡概率时不作处于危险数校正外，与Berkson-Gage寿命表相同。结果 两者都有还原性；前者有自相容性，后者没有；前者几乎无偏性，后者严重低估；前者比后者有效。结论 建议用无校正寿命表取代Berkson-Gage寿命表。
The Berkson-Gage Life Table and the Unadjusted Life Table
Zhao Guolong,Henan Medical University (450052) ,Zhengzhou
, 百拇医药
【Abstract】 Objective This paper proposes the unadjusted life table and compares it with the Berkson-Gage life table.Methods Its structure is the same as the Berkson-Gage life table except that the adjustment of the number at risk is omitted in calculating the conditional probability dying.Results The unadjusted life table and the Berkson-Gage life table are both reducible.The former possesses the property of self-consistency but the latter does not.The former is almost unbiased but the latter strictly underestimated.And the former is more efficient than the latter.Conclusion Thus it is suggested to use the unadjusted life table in place of the Berkson-Gage life table.
, http://www.100md.com
【Key words】 Censorship Efficiency Life table Self-consistency Survival rate Unbiasedness
Berkson-Gage寿命表〔1-6〕早已为人们所熟知。它有两个要点：①由时间区间下限人数减去终检数的一半作校正。②生存率估计值被认为定位于区间上限。
然而在近年实践中发现，同时用Kaplan-Meier法和Berkson-Gage法就同一宗资料估计生存率，后者往往较低(详后)。既然前者被认为是渐近无偏的〔7〕，后者难道是低估了?实践也显示，取消校正，后者升高。同时可证明，生存率估计值定位于区间中点。
本文首先取消校正，制成无校正寿命表，然后同Berkson-Gage寿命表作以比较。
无校正寿命表
, http://www.100md.com
设观测的样本为(TI，ΔI)，I=1，…，N，这里TI是观测的时间，若ΔI=1，TI是死亡时间，ΔI=0，终检时间，N是样本量。制作寿命表需4个步骤。
第1步，编排寿命表阶。将观测值排序得次序统计量(T′I，Δ′I)，T′1<…N。由T′N和时间区间宽度h得寿命表阶数
M=INT(T′N/h)+1
这里0N，M≤N。由此列出i=1，…，M个寿命表阶。
第2步，数认属于第i阶的观测值数。由
, 百拇医药
i=INT(T′I/h)+1
(1)
知T′I属于第i阶。如此共有ai个T′I′s属于该阶。这包括di个死亡和ai-di个终检值数，这里di是T′I′s对应Δ′I′s的和。
第3步，估计第i阶生存率。第j,j=1，…，i,阶处于危险数为
(2)
第i阶生存率估计为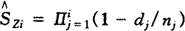
, http://www.100md.com
(3)
第4步，确定时间点。(1)可写成INT(TI′/h)=i-1。这是TI′/h的整数部分，其小数部分为CI=TI′/h-INT(TI′/h),CI∈〔0，1)，故有
如此形成第i阶时间区间[(i-1)h,(i-0.5)h,ih)。设ti-1=(i-1)h,tmi=(i-0.5)h,ti=ih得t0=0,tmi=
(ti-1+ti),该区间亦可写成[ti-1,tmi,ti)。将CI的期望看作E(CI)=0.5，得TI′的期望E(TI′)=(i-0.5)h=tmi。可见这种转换的机制是由ai个T′I′S(较小时间单位)经(1)得其期望tmi(较大单位)。因此由(3)得到的是第i阶区间中点tmi的生存率估计值
, 百拇医药
(4)
这就是无校正寿命表。它与Berkson-Gage寿命表
rj=nj-(aj-dj)的区别是取消了校正-(aj-dj)。
Kaplan-Meier寿命表
为了解无校正寿命表的性质，宜将它与Kaplan-Meier寿命表进行逐阶比较，对应采取4个步骤。
, 百拇医药
第1步，编排寿命表阶。时间区间宽度h在此成为时间单位转换系数h。取值相同，所得较大单位相同。经
i=INT(T′I/h+0.5)
(5)
形成i=1，…，M个寿命表阶。
第2步，计算各阶观测值重合数。由(5)知T′I属第i阶。如此属该阶的T′I′S共有ai个，包括di个死亡和ai-di个终检值数。
第3步，估计第i阶生存率。由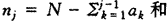
, 百拇医药
(6)
得第i阶Kaplan-Meier估计值。
第4步，确定时间点。(5)是TI′/h+0.5的整数部分，其小数部分是CI=TI′/h+0.5-INT(TI′/h+0.5)，CI∈[0，1)，故有TI′=(i+CI-0.5)h。以E(CI)=0.5得E(TI′)=ih=ti。因此
i定位于时间点ti：(ti)=i。这就是有重合生存资料Kaplan-Meier寿命表。
, http://www.100md.com
由无重合转换成有重合的机制是由ai个T′I′S(较小时间单位)经(5)得其期望ti(较大单位)。这与纳入时间区间的机制相同，由
得第i阶区间[(i-0.5)h,ih,(i+0.5)h。可见，所确定的时间点正是区间中点。其前半与无校正寿命表区间后半重合。为便于比较，按
(7)
得tmi点的近似值。在无终检和均匀分布时，(7)是精确等式，且有Z(tmi)=(tmi)，证明从略。
, http://www.100md.com
至此，无校正估计值定位于区间中点{tmi}的依据有①Kaplan-Meier估计值对应的时间点是区间中点，无校正估计值也应如此，由于有重合样本的形成与时间区间的形成有相同的机制；②在无终检和均匀分布时，第i阶无校正估计值等于tmi点Kaplan-Meier估计值；③用(1)代替(5)亦可制作Kaplan-Meier寿命表，并直接得到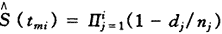
这与(3)在字面上相同，计算结果也相同。前两点也适于Berkson-Gage估计值。这提示，以往关于它定位于区间上限的说法是一种误解。
基本性质
与Berkson-Gage寿命表相比，无校正寿命表的要点是，①不用校正，②生存率估计值定位于区间中点。其基本性质如下。
, 百拇医药
1.还原性
式(3)是条件生存概率连乘式。无终检时每阶的分子等于其后一阶的分母，辗转对销后得经验分布函数的补。这就是说，生存率的无校正估计值具有还原性〔8〕，至于Berkson-Gage估计值，当无终检时，校正项-(aj-dj)=0，同样可证明具有还原性。
2.自相容性
设在寿命表第i阶生存率估计为i，由此估计截止该阶的存活数为
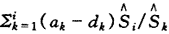，活过第i阶的病人数为
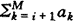，从而复得生存率估计值
, 百拇医药
(8)
一般说来，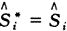
，这就是生存率估计值的自相容性〔9〕。经简单代数转换可证明
，这就是说，无校正估计值具有自相容性。至于Berkson-Gage估计值B(tmi)，结果为
，没有这种性质。
3.无偏性
Kaplan-Meier估计值被证明是渐近无偏的〔7〕。根据这一性质，利用足够大样本通过足够多次抽样产生的平均Kaplan-Meier估计值可被看作是生存率真值。同样条件下产生的平均无校正估计值可被看作是生存率期望值，以此提示后者有无偏性。
, 百拇医药
取样本量N=30，60，90在Weibull死亡和均匀终检时间分布下抽样并使各试验集平均观测终检率为0.1，0.2，0.3，0.4，0.5。取h=0.1,0.2,0.3,0.6计算无校正估计值Z(tmi)，Berkson-Gage估计值B(tmi)，和Kaplan-Meier估计值(tmi)。由不同样本量，不同死亡和终检时间分布，不同时间点，不同h值交叉组合，各执行1 000次独立试验。由此得平均值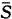
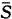Z，B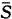，。前两者被看作期望值SZ，SB，后者被看作生存率真值π。偏性表达为QZ=SZ-π，QB=SB-π。
, 百拇医药
结果表明，在无终检时，QZ=QB，有终检时，QZ围绕在零左右，而QB为负值。随终检率上升，QZ变化不明显，而QB呈负向增长。这说明，不管有无终检，无校正估计值几乎无偏，而基于终检分布Berkson-Gage估计值低估，其偏性随终检率升高而趋于严重。
4.相对有效性
设无校正估计值的同源方差估计值〔8〕为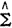
Z2(tmi)。对于Berkson-Gage估计值，这是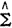B2(tmi)。各试验集产生的平均值
Z2，B2被看作期望值
，
。这里，Z对B的相对有效性表达为
, http://www.100md.com
(9)
结果表明，在无终检时，RH=1；有终检时，RH>1。随终检率升高，RH值升高。这说明，在无终检时，二者有相等的有效性；有终检时，无校正估计值比Berkson-Gage估计值有效。相对有效性随终检率升高。
改用Greenwood估计值，结果相同，且能更有力地展示无校正估计值比Berkson-Gage估计值有效。
实 例
这里再次引用17例口咽鳞癌病人的生存时间(天)〔10〕。时间区间宽度取h=365.25，按(1)～(4)式制成无校正寿命表，见表1。由(8)得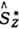
(tmi)，可见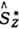(tmi)=Z(tmi)。表内亦显示B*(tmi)>B(tmi)。说明Z(tmi)具有自相容性，而B(tmi)没有。由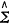
Z2(tmi)<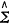B2(tmi)，
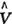Z2(tmi)<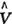B2(tmi)提示Z(tmi)比B(tmi)有效，不管按同源生存率方差估计公式还是Greenwood公式皆然。时间单位转换系数亦取h=365.25，计算Kaplan-Meier估计值为(tmi)={0.706，0.431，0.353，0.314，0.314}，可见Z(tmi)十分接近(tmi)，而B(tmi)明显低于(tmi)。这提示，Z(tmi)偏性很小，而B(tmi)严重低估。
, http://www.100md.com
由该例看出，无校正估计值在各阶均高于Berkson-Gage估计值。
表1 17例口咽鳞癌病人的无校正寿命表和Berkson-Gage寿命表 寿命表
阶数
i
生存时
间(年)
[ti-1,ti]
处于危
险人数
ni
观测值
, http://www.100md.com
重合数
ai
死亡
数(di)
无校正
估计值
Berkson-Gage
估计值
同源生存率
方差估计值*
Greenwood
方差估计值*Z(tmi)
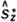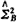(tmi)B(tmi)
(tmi)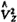
(tmi)
(tmi)
(tmi)
(tmi)
, 百拇医药
1
[0，1)
17
6
5
0.706
0.706
0.697
0.706
0.122
0.128
0.122
0.131
, http://www.100md.com
2
[1，2)
11
6
5
0.385
0.385
0.365
0.384
0.152
0.154
0.149
0.167
, 百拇医药
3
[2，3)
5
2
1
0.308
0.308
0.284
0.305
0.164
0.165
0.143
0.167
, http://www.100md.com
4
[3，4)
3
2
0
0.308
0.308
0.284
0.305
0.219
0.289
0.143
0.167
, 百拇医药
5
[4，5)
1
1
0
0.308
0.308
0.284
0.305
0.657
1.155
0.143
0.167
, 百拇医药
*栏下数据是原数值的10倍。讨 论
这项工作产生的认识是，无校正寿命表优于Berkson-Gage寿命表。前者具有还原性，自相容性，几乎无偏性，且比后者有效。相比之下，后者尽管也有还原性，却没有自相容性，严重低估，且相对效率低下。
Berkson-Gage寿命表的这些不良性质归因于该校正，然而在长达半个世纪实践中一直未能揭露。这是由于区间上限生存率低于区间中点，该校正酿成对生存率的低估被误认为它定位于区间上限所掩盖。这一揭露只是在找到了就Berkson-Gage寿命表同Kaplan-Meier寿命表进行逐阶比较的方法，才得以实现。
因此，这项工作的理论意义在于它揭露出该校正和将生存率估计值定位于区间上限的错误，其临床意义是所提出的方法优于旧有方法且十分常用。建议用无校正寿命表取代Berkson-Gage寿命表。在制作寿命表时宜适当安排时间区间以获得所需时间点。
, http://www.100md.com
参考文献
1.Berkson J,Gage,RP.Calculation of survival rates for cancer.Proceedings of the Staff Meetings of the Mayo Clinic,1950，25:270.
2.Chiang CL.Introduction to stochastic processes in biostatistics.New York:John Wiley and Sons,1968.
3.Cutler SJ.Ederer F.Maximum utilization of the life table method in analyzing survival.J Chron Dis, 1958,8:699.
4.Elveback L.Actuarial estimation of survivorship in chronic disease.J Am Stat Ass 1958,53:420.
, 百拇医药
5.Gehan EA.Estimating survival functions from the life table.J Chron Dis,1969,21:629.
6.Littell AS.Estimation of the T-year survival rate from follow-up studies over a limited period of time.Human Biology,1952,24:87.
7.Fleming TR,Harrington DP.Nonparametric estimation of the survival distribution in censored data.Communications in Statistics-Simulation and Computation,1984,13:2469.
8.Zhao G.The homogenetic estimate for the variance of survival rate.Statistics in Medicine,1996,15:51.
9.Efron B.The two sample problem with censored data.Proceedings of the 5th Berkley Symposium on Mathematical statistics and Probability 1967,4:831.
10.Dykstra RL,Feltz CJ.Nonparametric maximum likelihood estimation of survival functions with a general stochastic ordering and its dual.Biometrika,1989,76:331., http://www.100md.com
单位：河南医科大学(450052)
关键词：终检；有效性；寿命表；自相容性；生存率；无偏性
中国卫生统计990503 【提 要】 目的 本文提出无校正寿命表，并同Berkson-Gage寿命表作以比较。方法 其构造，除在计算条件死亡概率时不作处于危险数校正外，与Berkson-Gage寿命表相同。结果 两者都有还原性；前者有自相容性，后者没有；前者几乎无偏性，后者严重低估；前者比后者有效。结论 建议用无校正寿命表取代Berkson-Gage寿命表。
The Berkson-Gage Life Table and the Unadjusted Life Table
Zhao Guolong,Henan Medical University (450052) ,Zhengzhou
, 百拇医药
【Abstract】 Objective This paper proposes the unadjusted life table and compares it with the Berkson-Gage life table.Methods Its structure is the same as the Berkson-Gage life table except that the adjustment of the number at risk is omitted in calculating the conditional probability dying.Results The unadjusted life table and the Berkson-Gage life table are both reducible.The former possesses the property of self-consistency but the latter does not.The former is almost unbiased but the latter strictly underestimated.And the former is more efficient than the latter.Conclusion Thus it is suggested to use the unadjusted life table in place of the Berkson-Gage life table.
, http://www.100md.com
【Key words】 Censorship Efficiency Life table Self-consistency Survival rate Unbiasedness
Berkson-Gage寿命表〔1-6〕早已为人们所熟知。它有两个要点：①由时间区间下限人数减去终检数的一半作校正。②生存率估计值被认为定位于区间上限。
然而在近年实践中发现，同时用Kaplan-Meier法和Berkson-Gage法就同一宗资料估计生存率，后者往往较低(详后)。既然前者被认为是渐近无偏的〔7〕，后者难道是低估了?实践也显示，取消校正，后者升高。同时可证明，生存率估计值定位于区间中点。
本文首先取消校正，制成无校正寿命表，然后同Berkson-Gage寿命表作以比较。
无校正寿命表
, http://www.100md.com
设观测的样本为(TI，ΔI)，I=1，…，N，这里TI是观测的时间，若ΔI=1，TI是死亡时间，ΔI=0，终检时间，N是样本量。制作寿命表需4个步骤。
第1步，编排寿命表阶。将观测值排序得次序统计量(T′I，Δ′I)，T′1<…
M=INT(T′N/h)+1
这里0
第2步，数认属于第i阶的观测值数。由
, 百拇医药
i=INT(T′I/h)+1
(1)
知T′I属于第i阶。如此共有ai个T′I′s属于该阶。这包括di个死亡和ai-di个终检值数，这里di是T′I′s对应Δ′I′s的和。
第3步，估计第i阶生存率。第j,j=1，…，i,阶处于危险数为
(2)
第i阶生存率估计为
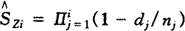
, http://www.100md.com
(3)
第4步，确定时间点。(1)可写成INT(TI′/h)=i-1。这是TI′/h的整数部分，其小数部分为CI=TI′/h-INT(TI′/h),CI∈〔0，1)，故有
如此形成第i阶时间区间[(i-1)h,(i-0.5)h,ih)。设ti-1=(i-1)h,tmi=(i-0.5)h,ti=ih得t0=0,tmi=
(ti-1+ti),该区间亦可写成[ti-1,tmi,ti)。将CI的期望看作E(CI)=0.5，得TI′的期望E(TI′)=(i-0.5)h=tmi。可见这种转换的机制是由ai个T′I′S(较小时间单位)经(1)得其期望tmi(较大单位)。因此由(3)得到的是第i阶区间中点tmi的生存率估计值, 百拇医药
(4)
这就是无校正寿命表。它与Berkson-Gage寿命表
rj=nj-
(aj-dj)的区别是取消了校正-(aj-dj)。Kaplan-Meier寿命表
为了解无校正寿命表的性质，宜将它与Kaplan-Meier寿命表进行逐阶比较，对应采取4个步骤。
, 百拇医药
第1步，编排寿命表阶。时间区间宽度h在此成为时间单位转换系数h。取值相同，所得较大单位相同。经
i=INT(T′I/h+0.5)
(5)
形成i=1，…，M个寿命表阶。
第2步，计算各阶观测值重合数。由(5)知T′I属第i阶。如此属该阶的T′I′S共有ai个，包括di个死亡和ai-di个终检值数。
第3步，估计第i阶生存率。由
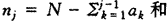
, 百拇医药
(6)
得第i阶Kaplan-Meier估计值。
第4步，确定时间点。(5)是TI′/h+0.5的整数部分，其小数部分是CI=TI′/h+0.5-INT(TI′/h+0.5)，CI∈[0，1)，故有TI′=(i+CI-0.5)h。以E(CI)=0.5得E(TI′)=ih=ti。因此
i定位于时间点ti：(ti)=i。这就是有重合生存资料Kaplan-Meier寿命表。, http://www.100md.com
由无重合转换成有重合的机制是由ai个T′I′S(较小时间单位)经(5)得其期望ti(较大单位)。这与纳入时间区间的机制相同，由
得第i阶区间[(i-0.5)h,ih,(i+0.5)h。可见，所确定的时间点正是区间中点。其前半与无校正寿命表区间后半重合。为便于比较，按
(7)
得tmi点的近似值。在无终检和均匀分布时，(7)是精确等式，且有
Z(tmi)=(tmi)，证明从略。, http://www.100md.com
至此，无校正估计值定位于区间中点{tmi}的依据有①Kaplan-Meier估计值对应的时间点是区间中点，无校正估计值也应如此，由于有重合样本的形成与时间区间的形成有相同的机制；②在无终检和均匀分布时，第i阶无校正估计值等于tmi点Kaplan-Meier估计值；③用(1)代替(5)亦可制作Kaplan-Meier寿命表，并直接得到
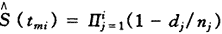
这与(3)在字面上相同，计算结果也相同。前两点也适于Berkson-Gage估计值。这提示，以往关于它定位于区间上限的说法是一种误解。
基本性质
与Berkson-Gage寿命表相比，无校正寿命表的要点是，①不用校正，②生存率估计值定位于区间中点。其基本性质如下。
, 百拇医药
1.还原性
式(3)是条件生存概率连乘式。无终检时每阶的分子等于其后一阶的分母，辗转对销后得经验分布函数的补。这就是说，生存率的无校正估计值具有还原性〔8〕，至于Berkson-Gage估计值，当无终检时，校正项-
(aj-dj)=0，同样可证明具有还原性。2.自相容性
设在寿命表第i阶生存率估计为
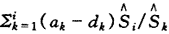i，由此估计截止该阶的存活数为，活过第i阶的病人数为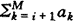，从而复得生存率估计值, 百拇医药
(8)
一般说来，
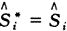，这就是生存率估计值的自相容性〔9〕。经简单代数转换可证明，这就是说，无校正估计值具有自相容性。至于Berkson-Gage估计值B(tmi)，结果为，没有这种性质。3.无偏性
Kaplan-Meier估计值被证明是渐近无偏的〔7〕。根据这一性质，利用足够大样本通过足够多次抽样产生的平均Kaplan-Meier估计值可被看作是生存率真值。同样条件下产生的平均无校正估计值可被看作是生存率期望值，以此提示后者有无偏性。
, 百拇医药
取样本量N=30，60，90在Weibull死亡和均匀终检时间分布下抽样并使各试验集平均观测终检率为0.1，0.2，0.3，0.4，0.5。取h=0.1,0.2,0.3,0.6计算无校正估计值
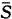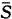Z(tmi)，Berkson-Gage估计值B(tmi)，和Kaplan-Meier估计值(tmi)。由不同样本量，不同死亡和终检时间分布，不同时间点，不同h值交叉组合，各执行1 000次独立试验。由此得平均值Z，B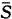，。前两者被看作期望值SZ，SB，后者被看作生存率真值π。偏性表达为QZ=SZ-π，QB=SB-π。, 百拇医药
结果表明，在无终检时，QZ=QB，有终检时，QZ围绕在零左右，而QB为负值。随终检率上升，QZ变化不明显，而QB呈负向增长。这说明，不管有无终检，无校正估计值几乎无偏，而基于终检分布Berkson-Gage估计值低估，其偏性随终检率升高而趋于严重。
4.相对有效性
设无校正估计值的同源方差估计值〔8〕为
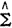Z2(tmi)。对于Berkson-Gage估计值，这是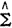B2(tmi)。各试验集产生的平均值Z2，B2被看作期望值，。这里，Z对B的相对有效性表达为, http://www.100md.com
(9)
结果表明，在无终检时，RH=1；有终检时，RH>1。随终检率升高，RH值升高。这说明，在无终检时，二者有相等的有效性；有终检时，无校正估计值比Berkson-Gage估计值有效。相对有效性随终检率升高。
改用Greenwood估计值，结果相同，且能更有力地展示无校正估计值比Berkson-Gage估计值有效。
实 例
这里再次引用17例口咽鳞癌病人的生存时间(天)〔10〕。时间区间宽度取h=365.25，按(1)～(4)式制成无校正寿命表，见表1。由(8)得
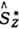(tmi)，可见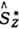(tmi)=Z(tmi)。表内亦显示B*(tmi)>B(tmi)。说明Z(tmi)具有自相容性，而B(tmi)没有。由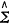Z2(tmi)<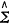B2(tmi)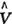，Z2(tmi)<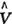B2(tmi)提示Z(tmi)比B(tmi)有效，不管按同源生存率方差估计公式还是Greenwood公式皆然。时间单位转换系数亦取h=365.25，计算Kaplan-Meier估计值为(tmi)={0.706，0.431，0.353，0.314，0.314}，可见Z(tmi)十分接近(tmi)，而B(tmi)明显低于(tmi)。这提示，Z(tmi)偏性很小，而B(tmi)严重低估。, http://www.100md.com
由该例看出，无校正估计值在各阶均高于Berkson-Gage估计值。
表1 17例口咽鳞癌病人的无校正寿命表和Berkson-Gage寿命表 寿命表
阶数
i
生存时
间(年)
[ti-1,ti]
处于危
险人数
ni
观测值
, http://www.100md.com
重合数
ai
死亡
数(di)
无校正
估计值
Berkson-Gage
估计值
同源生存率
方差估计值*
Greenwood
方差估计值*
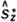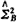Z(tmi)(tmi)B(tmi)(tmi)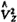(tmi)(tmi)(tmi)(tmi), 百拇医药
1
[0，1)
17
6
5
0.706
0.706
0.697
0.706
0.122
0.128
0.122
0.131
, http://www.100md.com
2
[1，2)
11
6
5
0.385
0.385
0.365
0.384
0.152
0.154
0.149
0.167
, 百拇医药
3
[2，3)
5
2
1
0.308
0.308
0.284
0.305
0.164
0.165
0.143
0.167
, http://www.100md.com
4
[3，4)
3
2
0
0.308
0.308
0.284
0.305
0.219
0.289
0.143
0.167
, 百拇医药
5
[4，5)
1
1
0
0.308
0.308
0.284
0.305
0.657
1.155
0.143
0.167
, 百拇医药
*栏下数据是原数值的10倍。讨 论
这项工作产生的认识是，无校正寿命表优于Berkson-Gage寿命表。前者具有还原性，自相容性，几乎无偏性，且比后者有效。相比之下，后者尽管也有还原性，却没有自相容性，严重低估，且相对效率低下。
Berkson-Gage寿命表的这些不良性质归因于该校正，然而在长达半个世纪实践中一直未能揭露。这是由于区间上限生存率低于区间中点，该校正酿成对生存率的低估被误认为它定位于区间上限所掩盖。这一揭露只是在找到了就Berkson-Gage寿命表同Kaplan-Meier寿命表进行逐阶比较的方法，才得以实现。
因此，这项工作的理论意义在于它揭露出该校正和将生存率估计值定位于区间上限的错误，其临床意义是所提出的方法优于旧有方法且十分常用。建议用无校正寿命表取代Berkson-Gage寿命表。在制作寿命表时宜适当安排时间区间以获得所需时间点。
, http://www.100md.com
参考文献
1.Berkson J,Gage,RP.Calculation of survival rates for cancer.Proceedings of the Staff Meetings of the Mayo Clinic,1950，25:270.
2.Chiang CL.Introduction to stochastic processes in biostatistics.New York:John Wiley and Sons,1968.
3.Cutler SJ.Ederer F.Maximum utilization of the life table method in analyzing survival.J Chron Dis, 1958,8:699.
4.Elveback L.Actuarial estimation of survivorship in chronic disease.J Am Stat Ass 1958,53:420.
, 百拇医药
5.Gehan EA.Estimating survival functions from the life table.J Chron Dis,1969,21:629.
6.Littell AS.Estimation of the T-year survival rate from follow-up studies over a limited period of time.Human Biology,1952,24:87.
7.Fleming TR,Harrington DP.Nonparametric estimation of the survival distribution in censored data.Communications in Statistics-Simulation and Computation,1984,13:2469.
8.Zhao G.The homogenetic estimate for the variance of survival rate.Statistics in Medicine,1996,15:51.
9.Efron B.The two sample problem with censored data.Proceedings of the 5th Berkley Symposium on Mathematical statistics and Probability 1967,4:831.
10.Dykstra RL,Feltz CJ.Nonparametric maximum likelihood estimation of survival functions with a general stochastic ordering and its dual.Biometrika,1989,76:331., http://www.100md.com