适用于一类医学动态监测数据的稳健参数估计方法*试论原子生态学成为一门生态学分支学科的可能性
作者:王磊 郑崇勋 龚均 张茹
单位:王磊 郑崇勋 西安交通大学生物医学工程研究所(710049); 龚均 张茹 西安医科大学第二临床学院
关键词:稳健;参数估计;动态监测;分布拟合
中国卫生统计990502 【提 要】 目的 介绍并分析适用于一类医学动态监测数据的稳健参数估计方法。方法 结合分布假设和稳健统计给出了参数估计方法。首次提出一种迭代求取形状参数稳健估计的算法。结果 该方法对医学动态监测中某生理量异常所占百分比值统计量的参数估计优于临床普遍采用的方法。结论 通过对分布拟合、估计优效性和可实现性、估计稳健性等理论分析和模拟实验,表明该方法是一种高效、可靠的稳健参数估计方法。
The Robust Parameter Estimation Method Applied to a Class of
, 百拇医药
Medical Dynamic Monitoring Data
、Wang Lei,Zheng Chongxun
Xi'an JiaoTong University Biomedical Engineering Institute(710049),Xi'an
【Abstract】 Objective A robust parameter estimation method applied to a class of medical dynamic monitoring data is introduced and analyzed in this paper.Methods This parameter estimation method is introduced by being combined with distribution hypothesis and robust statistics.The iteration algorithm to estimate shape-parameter is first present.Results For the parameter estimation of percent statistic relating to abnormality of some physiologic value during dynamic monitoring,we confirm that this method precedes the method generally used by clinic.Conclusion This method is of high credibility and efficiency after the theory analysis and simulation test of the goodness-of-fit of distribution,merit and workability and robustness of estimation statistic.
, http://www.100md.com
【Key words】 Robustness Parameter estimation Dynamic Monitoring Goodness-of-fit of distribution
对于正偏态分布的总体,采用对数转换或其他趋势曲线〔1〕将其正态化,从而用样本均值和标准差来估计总体期望和方差的方法虽比较普遍,但却缺乏理论依据,且在很多情况下效果一般。Weibull分布具有与正偏态样本拟合优度好、信息量丰富等特点,许多医学统计量服从或近似服从该分布〔2〕。一般的参数估计方法只考虑理想情况(样本独立同分布于理想模型)下的估计效果,但实际上由于总体不一定与假设严格相符、样本未必来自同一总体等原因〔3〕,必须要考虑估计方法的稳健性。本文针对所举统计量,通过拟合实验进行Weibull分布的假设检验,并且设计出一种合适的稳健参数估计方法。
方 法
, 百拇医药
Weibull分布的概率密度函数为f(x)=α/β(x-δ)α-1.e-(x-δ)α/β,x≥δ,其中δ≥0为位置参数,α>0为形状参数,β>0为刻度参数,期望EX=Γ(1+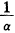 ).β1/α+δ,方差DX=(Γ(1+2/α)-Γ2(1+1/α)).β2/α(Γ(x)表示Gamma函数)。当α=1时Weibull分布化为指数分布。
).β1/α+δ,方差DX=(Γ(1+2/α)-Γ2(1+1/α)).β2/α(Γ(x)表示Gamma函数)。当α=1时Weibull分布化为指数分布。
首先分析分布假设。数据来自1994~1999年3月西安医科大学第二临床学院消化内科对主述烧心、胃食道返流等症状的就诊者所做的24小时食管pH动态监测,共165例(其中男86例,女79例,平均年龄41岁),取每例数据pH<4所占检测时间百分比值作为样本(目前临床将食道pH<4判断为胃食道返流,且认为pH<4占监测时间百分比值对判断胃食道返流具有最好的特异性〔4〕。样本频数图直观地表明样本呈明显正偏态——单边“厚尾”分布。绘在正态概率纸、Weibull概率纸上的拟合图表明样本与正态分布的拟合程度差,与Weibull分布的拟合程度较好,t检验、Kolmogorov检验、峰度——偏度联合检验等检验方法进一步肯定上述分析。另外由ω统计量〔5〕得样本与Weibull分布的拟合程度要优于与对数正态分布的拟合程度。
, 百拇医药
图1 样本的频数图
尽管计算机数据采集技术可将读数错误、记录错误等减小到最低限度,但由于监测时间长,监测环境复杂等原因,样本中必定存在一定数量的异常值〔4〕,对异常值分布我们所知甚少。同时考虑到前述分布假设及对其的猜测成分,使得简单应用样本均值和标准差的参数估计方法必将存在较大误差。我们结合次序统计量和稳健统计,在假设总体具有有限期望和方差的前提下,设计如下的稳健参数估计方法:
对样本y1、y2…、yN从小到大排序得y〔1〕、y〔2〕、…y〔N〕。直接求得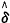 =y〔1〕。令x〔i〕=y〔i〕-y〔1〕,i=1,…,N。计算对较大一侧单边截尾θ后的样本一、二阶原点矩统计量
=y〔1〕。令x〔i〕=y〔i〕-y〔1〕,i=1,…,N。计算对较大一侧单边截尾θ后的样本一、二阶原点矩统计量
 ,之后利用等式Γ(1+2/
,之后利用等式Γ(1+2/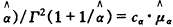 (cα为与
(cα为与 有关的无偏因子)迭代求取
有关的无偏因子)迭代求取 。最后令
。最后令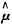 α1=cα1
α1=cα1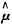 1(cα1为
1(cα1为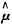 1的无偏因子)、
1的无偏因子)、 ,得到
,得到
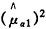 。估计结果见下表1。
。估计结果见下表1。
, 百拇医药
表1 稳健参数估计结果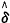


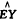
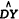
θ=5%
0
0.411
0.227
0.083
0.059
, 百拇医药
θ=10%
0
0.42
0.222
0.081
0.053
讨 论
百分比统计量的有效取值范围应为0≤x≤1,而Weibull分布的定义域为δ≤x≤∞,两者并不一致。但考虑到由定义域变宽带来的误差很小,如当α=0.5,β=0.2,δ=0时,F(1) 0.995。为方便起见,我们并未修正Weibull分布的定义域。
0.995。为方便起见,我们并未修正Weibull分布的定义域。
不同的参数估计标准会产生极大似然估计、线性无偏和线性不变估计、矩估计等不同估计方法〔5〕。极大似然估计需求解联立超越方程,计算和分析有很大不便;线性估计方法则在很大程度上依赖不稳健的极大值分布,另外当样本值为0时其极值变换函数x=ln(t)无意义。相对而言,矩估计法是容易实现、便于稳健分析且当样本容量较大时效果较好的估计方法。上述分析的模拟实验见表2(Weibull分布样本由随机数发生器产生,分为150×250和2 500×15两组。不失一般性设δ=0、MSE=E(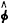 -φ)2,φ为待估参数)。
-φ)2,φ为待估参数)。
, 百拇医药
表2 模拟实验结果(实际值为所列值乘10-4) 估计
方法
MSE
第一组
MSE
第一组
MSE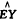
第一组
MSE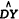
, 百拇医药
第一组
MSE
第二组
MSE
第二组
MSE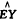
第二组
MSE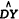
, 百拇医药
第二组
线性无偏
7.05
6.51
5.52
51.4
3.58
2.59
2.12
23.5
线性不变
6.82
6.30
, http://www.100md.com
5.46
49.4
3.46
2.58
2.03
23.1
最大似然
6.50
6.25
5.11
46.3
3.38
2.43
, 百拇医药
1.98
22.7
矩估计
7.25
6.72
5.71
55.1
3.62
2.66
2.18
24.5
总体服从W(α,β,δ)时,y〔1〕服从W(α,β/N,δ),当N→∞,y〔1〕将收敛到δ,即渐进无偏。另外,通过引入无偏因子可以保证 和
和 等估计统计量渐进无偏。故上述估计统计量的MSE应与渐进方差相同。对于矩法,
等估计统计量渐进无偏。故上述估计统计量的MSE应与渐进方差相同。对于矩法, 的方差达到Rao-Cramer下界β2/N,是最小方差无偏估计统计量;DY的估计统计量有
的方差达到Rao-Cramer下界β2/N,是最小方差无偏估计统计量;DY的估计统计量有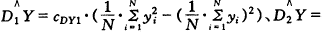
 (cDY等为无偏因子)等,当总体服从Weibull时,三者的渐进方差比见图2,我们选择在α≤1时渐进方差最小的
(cDY等为无偏因子)等,当总体服从Weibull时,三者的渐进方差比见图2,我们选择在α≤1时渐进方差最小的 做为DX的估计统计量。
做为DX的估计统计量。
, 百拇医药
图2 二阶矩估计统计量的方差比图
总体服从W(1,1/λ,0)时,f(x)=λN.NN/(N-1)!.xN-1.e-λ.N.x,x≥0,为均值统计量的概率密度。当N>100时该统计量可以95%的概率保证估计误差小于0.01,对其他较复杂的情况,模拟实验也得到相似结论。另外,对本文所举统计量来说,样本容量N过大会导致收集时间的延长、收集手段的不一致等,反而影响到样本的平稳性和参数估计的效果。我们认为N值的选择是合适的。
从泛函角度分析,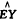 、
、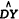 等几个估计统计量的影响函数〔3〕是广义有界的,而连续有界的影响函数对应对离群值不敏感及截断误差小的稳健估计统计量〔3〕。另由定义域知估计统计量
等几个估计统计量的影响函数〔3〕是广义有界的,而连续有界的影响函数对应对离群值不敏感及截断误差小的稳健估计统计量〔3〕。另由定义域知估计统计量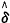 =y〔1〕稳健。median(X)和median|X-median(X)|、Winsor〔3〕化一、二阶矩等也都属于稳健统计量,计算它们与无偏矩估计法对污染和未污染的Weibull分布样本的参数估计的渐进方差,表明我们选择的单边截尾均值和单边截尾二阶矩的效果最好(表3)。
=y〔1〕稳健。median(X)和median|X-median(X)|、Winsor〔3〕化一、二阶矩等也都属于稳健统计量,计算它们与无偏矩估计法对污染和未污染的Weibull分布样本的参数估计的渐进方差,表明我们选择的单边截尾均值和单边截尾二阶矩的效果最好(表3)。
, 百拇医药
表3 不同总体下几种方法对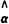 的渐进方差(实际值为所列值乘10-4) 设参数δ=0
的渐进方差(实际值为所列值乘10-4) 设参数δ=0
α=0.5
β=0.2
矩估
计法
θ=5%
单边
截尾
θ=5%
单边
Winsor
, 百拇医药
θ=5%
双边
截尾
θ=5%
双边
Winsor
θ=10%
单边
截尾
θ=10%
单边
Winsor
θ=10%
, http://www.100md.com
双边
截尾
θ=10%
双边
Winsor
中
位
数
W(α,β,δ)
9.63
1.75
1.92
1.75
, http://www.100md.com
1.94
1.70
1.82
1.70
1.81
14
0.95W(α,β,δ)+0.05W(2α,β,δ)
13
3.26
3.57
3.24
3.57
1.83
, 百拇医药
2.03
1.99
2.06
45
0.95W(α,β,δ)+0.05W(α,2β,δ)
47
13
16
13
17
6.91
8.67
6.97
, 百拇医药
8.56
233
0.95W(α,β,δ)+0.05U(0,1)
14
1.42
1.55
1.46
1.55
1.35
1.41
1.57
1.47
53
, http://www.100md.com
0.8W(α,β,δ)+0.2W(2α,β,δ)
56
23
27
23
26
8.77
12
10
13
254
对Weibull分布中形状参数的估计是对其他参数估计的基础 。由于分析繁复、无偏因子与分布参数有关等原因,形状参数的稳健估计鲜有报道。我们在矩估计法基础上设计的迭代算法,利用了weibull分布中形状参数的无偏因子仅与形状参数有关、形状参数的矩估计函数的单调性等特点,迭代求取形状参数的无偏稳健估计。由表3,与直接求取(不迭代)相比估计统计量的MSE要小一个数量级以上。结 论
, 百拇医药
本方法适用于医学动态监测中某生理量异常所占百分比值的统计量,这类统计量一般具有明显的正偏态分布、多数样本集中于较小一侧等特点。除文中分析的统计量外,24小时动态监测心电数据的ST段异常累计时间占监测时间百分比值(该值有重要临床意义)也属于此类。由于较好地结合了分布假设与稳健统计,本方法对此类统计量的参数估计优于临床普遍采用的方法。理论分析、模拟实验和实际应用表明其不失为一种高效、可靠的稳健参数估计方法。另外,随着动态监测技术的日益成熟和临床统计手段的深入发展,相信本方法会有更多的实际应用。
估计统计量的稳健性和效率是对立统一的关系,我们的目的是在可实现基础上寻找最优折衷,虽然一些具体的稳健方法已在临床上得到应用,但由于稳健统计的发展相对较短、灵活性大,这类应用还不十分成熟,我们所做的理论分析和模拟实验能为稳健统计提供一定的临床应用基础。接下来我们可通过搜集更全面的资料(包括正常组与确诊组的对照)来完善估计方法,在得到进一步结论的基础上可涉及假设检验等与置信概率有关的问题,从而针对临床比较系统地引入稳健分析。
, http://www.100md.com
*国家“八五”科技攻关项目及国家科委资助项目,项目编号925-30-04A。
参考文献
1.上海第一医学院卫生统计学教研组编.医学统计方法.上海:上海科学技术出版社,1979,160.
2.周士楷.威布尔分布在正偏态分布资料处理中的应用.中国卫生统计,1988,5(6):26.
3.Frank R.Hampel et al.Robust Estimation.John Wiley & Sons Inc.1986.
4.F Baldi,et al.Technical aspects of intraluminal pH-metry in man :current status and recommendations.Gut,1987,28:1177-1188.
5.戴树森,等.可靠性实验及其统计分布.国防工业出版社,1983,521.
中国微生态学杂志 2000年第4期第12卷 述评
试论原子生态学成为一门生态学分支学科的可能性
作者:向近敏 林雨霖 周峰 刘军 黄晓玲 李宗山
单位:湖北医科大学 病毒研究所暨分子生态学研究室,湖北 武昌430071
关键词:, 百拇医药
单位:王磊 郑崇勋 西安交通大学生物医学工程研究所(710049); 龚均 张茹 西安医科大学第二临床学院
关键词:稳健;参数估计;动态监测;分布拟合
中国卫生统计990502 【提 要】 目的 介绍并分析适用于一类医学动态监测数据的稳健参数估计方法。方法 结合分布假设和稳健统计给出了参数估计方法。首次提出一种迭代求取形状参数稳健估计的算法。结果 该方法对医学动态监测中某生理量异常所占百分比值统计量的参数估计优于临床普遍采用的方法。结论 通过对分布拟合、估计优效性和可实现性、估计稳健性等理论分析和模拟实验,表明该方法是一种高效、可靠的稳健参数估计方法。
The Robust Parameter Estimation Method Applied to a Class of
, 百拇医药
Medical Dynamic Monitoring Data
、Wang Lei,Zheng Chongxun
Xi'an JiaoTong University Biomedical Engineering Institute(710049),Xi'an
【Abstract】 Objective A robust parameter estimation method applied to a class of medical dynamic monitoring data is introduced and analyzed in this paper.Methods This parameter estimation method is introduced by being combined with distribution hypothesis and robust statistics.The iteration algorithm to estimate shape-parameter is first present.Results For the parameter estimation of percent statistic relating to abnormality of some physiologic value during dynamic monitoring,we confirm that this method precedes the method generally used by clinic.Conclusion This method is of high credibility and efficiency after the theory analysis and simulation test of the goodness-of-fit of distribution,merit and workability and robustness of estimation statistic.
, http://www.100md.com
【Key words】 Robustness Parameter estimation Dynamic Monitoring Goodness-of-fit of distribution
对于正偏态分布的总体,采用对数转换或其他趋势曲线〔1〕将其正态化,从而用样本均值和标准差来估计总体期望和方差的方法虽比较普遍,但却缺乏理论依据,且在很多情况下效果一般。Weibull分布具有与正偏态样本拟合优度好、信息量丰富等特点,许多医学统计量服从或近似服从该分布〔2〕。一般的参数估计方法只考虑理想情况(样本独立同分布于理想模型)下的估计效果,但实际上由于总体不一定与假设严格相符、样本未必来自同一总体等原因〔3〕,必须要考虑估计方法的稳健性。本文针对所举统计量,通过拟合实验进行Weibull分布的假设检验,并且设计出一种合适的稳健参数估计方法。
方 法
, 百拇医药
Weibull分布的概率密度函数为f(x)=α/β(x-δ)α-1.e-(x-δ)α/β,x≥δ,其中δ≥0为位置参数,α>0为形状参数,β>0为刻度参数,期望EX=Γ(1+
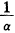 ).β1/α+δ,方差DX=(Γ(1+2/α)-Γ2(1+1/α)).β2/α(Γ(x)表示Gamma函数)。当α=1时Weibull分布化为指数分布。
).β1/α+δ,方差DX=(Γ(1+2/α)-Γ2(1+1/α)).β2/α(Γ(x)表示Gamma函数)。当α=1时Weibull分布化为指数分布。首先分析分布假设。数据来自1994~1999年3月西安医科大学第二临床学院消化内科对主述烧心、胃食道返流等症状的就诊者所做的24小时食管pH动态监测,共165例(其中男86例,女79例,平均年龄41岁),取每例数据pH<4所占检测时间百分比值作为样本(目前临床将食道pH<4判断为胃食道返流,且认为pH<4占监测时间百分比值对判断胃食道返流具有最好的特异性〔4〕。样本频数图直观地表明样本呈明显正偏态——单边“厚尾”分布。绘在正态概率纸、Weibull概率纸上的拟合图表明样本与正态分布的拟合程度差,与Weibull分布的拟合程度较好,t检验、Kolmogorov检验、峰度——偏度联合检验等检验方法进一步肯定上述分析。另外由ω统计量〔5〕得样本与Weibull分布的拟合程度要优于与对数正态分布的拟合程度。

, 百拇医药
图1 样本的频数图
尽管计算机数据采集技术可将读数错误、记录错误等减小到最低限度,但由于监测时间长,监测环境复杂等原因,样本中必定存在一定数量的异常值〔4〕,对异常值分布我们所知甚少。同时考虑到前述分布假设及对其的猜测成分,使得简单应用样本均值和标准差的参数估计方法必将存在较大误差。我们结合次序统计量和稳健统计,在假设总体具有有限期望和方差的前提下,设计如下的稳健参数估计方法:
对样本y1、y2…、yN从小到大排序得y〔1〕、y〔2〕、…y〔N〕。直接求得
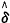 =y〔1〕。令x〔i〕=y〔i〕-y〔1〕,i=1,…,N。计算对较大一侧单边截尾θ后的样本一、二阶原点矩统计量
=y〔1〕。令x〔i〕=y〔i〕-y〔1〕,i=1,…,N。计算对较大一侧单边截尾θ后的样本一、二阶原点矩统计量
 ,之后利用等式Γ(1+2/
,之后利用等式Γ(1+2/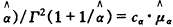 (cα为与
(cα为与 有关的无偏因子)迭代求取
有关的无偏因子)迭代求取 。最后令
。最后令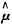 α1=cα1
α1=cα1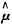 1(cα1为
1(cα1为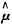 1的无偏因子)、
1的无偏因子)、 ,得到
,得到
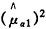 。估计结果见下表1。
。估计结果见下表1。, 百拇医药
表1 稳健参数估计结果
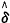


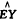
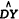
θ=5%
0
0.411
0.227
0.083
0.059
, 百拇医药
θ=10%
0
0.42
0.222
0.081
0.053
讨 论
百分比统计量的有效取值范围应为0≤x≤1,而Weibull分布的定义域为δ≤x≤∞,两者并不一致。但考虑到由定义域变宽带来的误差很小,如当α=0.5,β=0.2,δ=0时,F(1)
 0.995。为方便起见,我们并未修正Weibull分布的定义域。
0.995。为方便起见,我们并未修正Weibull分布的定义域。不同的参数估计标准会产生极大似然估计、线性无偏和线性不变估计、矩估计等不同估计方法〔5〕。极大似然估计需求解联立超越方程,计算和分析有很大不便;线性估计方法则在很大程度上依赖不稳健的极大值分布,另外当样本值为0时其极值变换函数x=ln(t)无意义。相对而言,矩估计法是容易实现、便于稳健分析且当样本容量较大时效果较好的估计方法。上述分析的模拟实验见表2(Weibull分布样本由随机数发生器产生,分为150×250和2 500×15两组。不失一般性设δ=0、MSE=E(
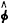 -φ)2,φ为待估参数)。
-φ)2,φ为待估参数)。, 百拇医药
表2 模拟实验结果(实际值为所列值乘10-4) 估计
方法
MSE

第一组
MSE

第一组
MSE
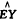
第一组
MSE
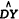
, 百拇医药
第一组
MSE

第二组
MSE

第二组
MSE
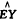
第二组
MSE
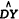
, 百拇医药
第二组
线性无偏
7.05
6.51
5.52
51.4
3.58
2.59
2.12
23.5
线性不变
6.82
6.30
, http://www.100md.com
5.46
49.4
3.46
2.58
2.03
23.1
最大似然
6.50
6.25
5.11
46.3
3.38
2.43
, 百拇医药
1.98
22.7
矩估计
7.25
6.72
5.71
55.1
3.62
2.66
2.18
24.5
总体服从W(α,β,δ)时,y〔1〕服从W(α,β/N,δ),当N→∞,y〔1〕将收敛到δ,即渐进无偏。另外,通过引入无偏因子可以保证
 和
和 等估计统计量渐进无偏。故上述估计统计量的MSE应与渐进方差相同。对于矩法,
等估计统计量渐进无偏。故上述估计统计量的MSE应与渐进方差相同。对于矩法, 的方差达到Rao-Cramer下界β2/N,是最小方差无偏估计统计量;DY的估计统计量有
的方差达到Rao-Cramer下界β2/N,是最小方差无偏估计统计量;DY的估计统计量有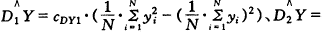
 (cDY等为无偏因子)等,当总体服从Weibull时,三者的渐进方差比见图2,我们选择在α≤1时渐进方差最小的
(cDY等为无偏因子)等,当总体服从Weibull时,三者的渐进方差比见图2,我们选择在α≤1时渐进方差最小的 做为DX的估计统计量。
做为DX的估计统计量。
, 百拇医药
图2 二阶矩估计统计量的方差比图
总体服从W(1,1/λ,0)时,f(x)=λN.NN/(N-1)!.xN-1.e-λ.N.x,x≥0,为均值统计量的概率密度。当N>100时该统计量可以95%的概率保证估计误差小于0.01,对其他较复杂的情况,模拟实验也得到相似结论。另外,对本文所举统计量来说,样本容量N过大会导致收集时间的延长、收集手段的不一致等,反而影响到样本的平稳性和参数估计的效果。我们认为N值的选择是合适的。
从泛函角度分析,
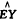 、
、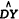 等几个估计统计量的影响函数〔3〕是广义有界的,而连续有界的影响函数对应对离群值不敏感及截断误差小的稳健估计统计量〔3〕。另由定义域知估计统计量
等几个估计统计量的影响函数〔3〕是广义有界的,而连续有界的影响函数对应对离群值不敏感及截断误差小的稳健估计统计量〔3〕。另由定义域知估计统计量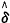 =y〔1〕稳健。median(X)和median|X-median(X)|、Winsor〔3〕化一、二阶矩等也都属于稳健统计量,计算它们与无偏矩估计法对污染和未污染的Weibull分布样本的参数估计的渐进方差,表明我们选择的单边截尾均值和单边截尾二阶矩的效果最好(表3)。
=y〔1〕稳健。median(X)和median|X-median(X)|、Winsor〔3〕化一、二阶矩等也都属于稳健统计量,计算它们与无偏矩估计法对污染和未污染的Weibull分布样本的参数估计的渐进方差,表明我们选择的单边截尾均值和单边截尾二阶矩的效果最好(表3)。, 百拇医药
表3 不同总体下几种方法对
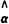 的渐进方差(实际值为所列值乘10-4) 设参数δ=0
的渐进方差(实际值为所列值乘10-4) 设参数δ=0α=0.5
β=0.2
矩估
计法
θ=5%
单边
截尾
θ=5%
单边
Winsor
, 百拇医药
θ=5%
双边
截尾
θ=5%
双边
Winsor
θ=10%
单边
截尾
θ=10%
单边
Winsor
θ=10%
, http://www.100md.com
双边
截尾
θ=10%
双边
Winsor
中
位
数
W(α,β,δ)
9.63
1.75
1.92
1.75
, http://www.100md.com
1.94
1.70
1.82
1.70
1.81
14
0.95W(α,β,δ)+0.05W(2α,β,δ)
13
3.26
3.57
3.24
3.57
1.83
, 百拇医药
2.03
1.99
2.06
45
0.95W(α,β,δ)+0.05W(α,2β,δ)
47
13
16
13
17
6.91
8.67
6.97
, 百拇医药
8.56
233
0.95W(α,β,δ)+0.05U(0,1)
14
1.42
1.55
1.46
1.55
1.35
1.41
1.57
1.47
53
, http://www.100md.com
0.8W(α,β,δ)+0.2W(2α,β,δ)
56
23
27
23
26
8.77
12
10
13
254
对Weibull分布中形状参数的估计是对其他参数估计的基础 。由于分析繁复、无偏因子与分布参数有关等原因,形状参数的稳健估计鲜有报道。我们在矩估计法基础上设计的迭代算法,利用了weibull分布中形状参数的无偏因子仅与形状参数有关、形状参数的矩估计函数的单调性等特点,迭代求取形状参数的无偏稳健估计。由表3,与直接求取(不迭代)相比估计统计量的MSE要小一个数量级以上。结 论
, 百拇医药
本方法适用于医学动态监测中某生理量异常所占百分比值的统计量,这类统计量一般具有明显的正偏态分布、多数样本集中于较小一侧等特点。除文中分析的统计量外,24小时动态监测心电数据的ST段异常累计时间占监测时间百分比值(该值有重要临床意义)也属于此类。由于较好地结合了分布假设与稳健统计,本方法对此类统计量的参数估计优于临床普遍采用的方法。理论分析、模拟实验和实际应用表明其不失为一种高效、可靠的稳健参数估计方法。另外,随着动态监测技术的日益成熟和临床统计手段的深入发展,相信本方法会有更多的实际应用。
估计统计量的稳健性和效率是对立统一的关系,我们的目的是在可实现基础上寻找最优折衷,虽然一些具体的稳健方法已在临床上得到应用,但由于稳健统计的发展相对较短、灵活性大,这类应用还不十分成熟,我们所做的理论分析和模拟实验能为稳健统计提供一定的临床应用基础。接下来我们可通过搜集更全面的资料(包括正常组与确诊组的对照)来完善估计方法,在得到进一步结论的基础上可涉及假设检验等与置信概率有关的问题,从而针对临床比较系统地引入稳健分析。
, http://www.100md.com
*国家“八五”科技攻关项目及国家科委资助项目,项目编号925-30-04A。
参考文献
1.上海第一医学院卫生统计学教研组编.医学统计方法.上海:上海科学技术出版社,1979,160.
2.周士楷.威布尔分布在正偏态分布资料处理中的应用.中国卫生统计,1988,5(6):26.
3.Frank R.Hampel et al.Robust Estimation.John Wiley & Sons Inc.1986.
4.F Baldi,et al.Technical aspects of intraluminal pH-metry in man :current status and recommendations.Gut,1987,28:1177-1188.
5.戴树森,等.可靠性实验及其统计分布.国防工业出版社,1983,521.
中国微生态学杂志 2000年第4期第12卷 述评
试论原子生态学成为一门生态学分支学科的可能性
作者:向近敏 林雨霖 周峰 刘军 黄晓玲 李宗山
单位:湖北医科大学 病毒研究所暨分子生态学研究室,湖北 武昌430071
关键词:, 百拇医药