对数线性模型的IPF算法及其软件实现
作者：张岩波 何大卫
单位：山西医科大学卫生统计教研室(030001)
关键词：高维列联表；对数线性模型；IPF算法
中国卫生统计990501 【提 要】 目的 采用Newton-Raphson法拟合对数线性模型时，如果列联表的维数太高(≥5)，使得设计矩阵复杂，以及迭代精度等原因，出现病态的信息矩阵，而无法收敛，导致算法失败。本文从应用角度探讨了IPF算法的有效性。方法 采用IPF算法对一个五维表进行了分析。结果 IPF算法能够很好地拟合高维表的模型，并得出了合理的结果。结论 IPF算法简便、稳健，在Newton-Raphson法失效时，不失为处理高维表的解决办法。
IPF Algorithm of Log-linear Model and Software Implement
, http://www.100md.com
Zhang Yanbo ,He Dawei.
Shanxi Medical University (030001),Taiyuan
【Abstract】 Objective When the Newton-Raphson algorithm is used to fit Log-linear model ,if the dimension of a contingency table is too high,it will make the design matrix complicated and present a ill-conditioned information matrix,in addition to the reason of iterative precision,The iteration can not converge and the N-R algorithm is failed.This paper discussed the IPF algorithm in practical aspect.Methods An example of 5-way table was Analyzed using IPF algorithm.Results IPF algorithm could effectively fit the model for high-way table and give a reasonable interpretation.Conclusion For IPF algorithm is simple and robust,it can yet be regarded as a method when the N-R algorithm has been failed.
, 百拇医药
【Key words】 High-way contingency table Log-linear model IPF algorithm
对数线性模型是分析高维列联表的得力工具。出于两种目的，对维数需要进行调整，①为便于解释而降维(减少分析变量)；②进行探索性分析时，在样本含量允许的情况下，希望引入多的变量，以期发现变量间更多的关系。考虑第二种情况，当维数太多时，若算法采用一般认为较优越的Newton-Raphson法(N-R法)其运算速度慢，更甚者，由于交互效应(参数)太多、设计矩阵复杂及迭代精度等原因，导致病态的信息短阵，无法求逆，而难于收敛，使得算法失败；迭代比例拟合算法(IPF算法)有参数估计算法复杂的缺点，但IPF法节省内存、运行速度快，而且求期望值算法简单、稳健，容易得出收敛的结果〔1〕。此时采用IPF法不失为一种解决的办法。本文偏重从应用角度来阐述IPF算法。
原理与方法
, 百拇医药
一、迭代比例拟合算法(Iterative Proportional Fitting Algorithm，IPFA)
IPF算法产生先于N-R法，由Deming和Stephan(1940)导出，后经Bishop(1969)、Haberman(1974)、Meyer(1981)等作过进一步改进，拓广〔1〕。在此以一个三维表的二阶模型为例，简述如何通过IPF算法迭代得出期望值。模型为：
(1)
m表示期望值，以“.”表示合计。由上式可知，各总计mij、mik和mjk受约束等于相应的观察边缘合计。迭代程序假定每个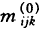
的初始值为1，然后按比例调整这些值，以满足第一个边缘约束mij=nij，计算公式为：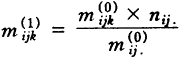
, 百拇医药
(2)
(其中：
)
再调整经修正的期望值，以满足另外两个边缘约束，即：mi.k=ni.k、m.jk=n.jk计算公式为：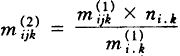
(3)
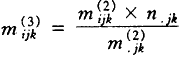
(4)
(其中：
)
, 百拇医药
至此，第一轮循环结束，将以上各值代入(2)式，开始第二轮循环，直至第t次循环达到收敛标准。即：任一格的第t和第t-1次循环的期望值之差小于某一常量ε。如：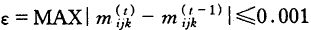
，这时可终止迭代。
对于一个模型，在模型中有多少个组态(Configuration)，则在每次循环中进行多少次运算。
二、模型的拟合优度检验
1、检验统计量：
(1)似然比统计量G2：G2=2Σyln(y/m)
(2)赤池信息量准则(AIC)：AIC=G2-2DF，便于多个模型拟合效果的比较，AIC越低，拟合效果越好。
, 百拇医药
2、 检验水准：本文采用同步检验过程(Simultaneous Test Procedure)〔2〕，即：γ=1-(1-α)k，k为零效应项数，采用γ的目的在于避免因检验水准选择太高而引进零效应，或检验水准太低而丢失显著的效应项。
3、最优模型筛选，采用Brown′s偏关联检验。
实例分析
例自Sewell与shan对Wisconsin的10 317名高中生是否计划上大学的一项调查，调查变量包括家庭的社会经济地位(socioeconomics status,低/中低/中高/高)、智力水平(Intelligence,低/中下/中上/高)、是否计划入学(Plan college,是/否)、性别(Sex,男/女)和父母重视鼓励程度(parental Encouragement,低/高)。5个变量分别以T、I、P、S、E表示构成4×4×2×2×2的高维表，见表1。
, 百拇医药
表1 高中生入学调查结果 计划入学
(P)
是
否
性 别
(E)
男
女
男
女
父母重视
(S)
高
, http://www.100md.com
低
高
低
高
低
高
低
地位(T)
智力(I)
低
低
4
13
5
, 百拇医药
9
349
64
455
44
中低
9
33
15
14
207
72
312
47
, http://www.100md.com
中高
12
38
8
20
126
54
216
35
高
10
89
13
28
, 百拇医药
67
43
96
24
中低
低
2
27
11
29
232
84
285
61
, 百拇医药
中低
7
64
19
47
201
95
236
88
中高
12
93
12
62
, 百拇医药
115
92
164
85
高
17
119
15
72
79
59
113
50
中高
, 百拇医药
低
8
47
7
36
164
91
163
72
中低
4
74
13
75
, 百拇医药
120
110
193
90
中高
17
148
12
91
92
100
174
100
, 百拇医药 高
6
198
20
142
42
73
81
77
高
低
4
39
16
, 百拇医药
36
48
57
50
58
中低
5
123
5
110
47
90
70
76
, 百拇医药
中高
9
224
13
230
41
65
47
81
高
8
414
13
360
, 百拇医药
17
54
49
98
对表1，采用IPF算法拟合一致阶模型如表2。表2 一致阶模型
模 型
G2
DF
P
检验水准γ
AIC
四维模型[TISP…IPSE
, http://www.100md.com
9.24
9
0.420
0.050
-8.76
三维模型[TIP TIS…PSE]
50.44
42
0.174
0.265
-33.56
二维模型[TI TS TP…SE]
, 百拇医药
138.85
88
0.000
0.560
-37.15
表2可见，模型3的拟合优度显然不能接受，模型2的AIC值较低，说明拟合效果较好，但P<0.265提示可能存在显著的四维交互效应项，因此对模型1，2分别筛选出不同的最优模型为：[PIST EST PE IE]、[PIS PIT IST EST PE IE]。表3为最优模型中各组态的似然比变化(ΔG2)。表3 最优模型各组态似然比变化 模型 1
模型 2
组态
, 百拇医药 ΔG2
DF
P
组态
ΔG2
DF
P
PIST
19.89
9
0.019
PIS
21.68
, 百拇医药
3
0.001
EST
9.95
3
0.019
PIT
19.64
9
0.020
PE
1640.28
1
, 百拇医药
0.000
IST
17.13
9
0.047
IE
145.08
3
0.000
EST
13.34
3
0.004
, 百拇医药
PE
1653.62
1
0.002
IE
144.97
3
0.000
G2=50.99 DF=52
P=0.514 γ=0.471
AIC=-53.01
G2=72.31 DF=64
, 百拇医药
P=0.22 γ=0.487
AIC=-55.69
通过IPF算法对五维表分析，得到了合理的结果。分析结果提示：各变量对入学态度都有不同的影响，其中智力、社会地位、性别与入学态度具有联合作用，父母鼓励重视程度对学生智力及是否入学具有较强的影响。以上两种模型理论上模型1是最佳的，但视实际情况或专业知识，模型2也可选。
利用IPF算法还可进一步借助饱和模型的参数及标准化残差进行分析。小 结
IPF算法计算简便，拟合一个包含R个组态的模型，在每次循环中只进行R次运算，大大节约运算时间，而且可以避免大量复杂的矩阵运算，因此算法稳健。文献报道，IPF算法迭代次数较少，本文实例，一般在10次左右即可达到迭代精度(ε=0.0001)。
对于普通列联表，N-R法和IPF算法往往分析结果一致，N-R法能详细得出参数估计的结果，因此对普通表本文仍提倡使用N-R法。但在进行探索性分析，需处理复杂的高维表时(如维数≥5或更多)，出于迭代精度及设计矩阵复杂的考虑，IPF算法不失为一种解决方法。
, 百拇医药
另外，在分析高维表时，由于变量关系复杂，不妨选择不同模型作为起始模型选出不同的最优模型，结合专业知识作出合理解释。
现行的统计软件中，SAS在CATMOD过程中提供了N-R法，IPF法也可用宏实现；SPSS具备两种算法拟合对数线性模型，特别后者采用IPF法及Brown's偏关联检验筛选最优模型，更是极大地方便了不熟悉模型的科研工作者分析应用。
参考文献
1.Santer T.J,Duffy D.E.The Statistical Analysis of Discrete Data.New York,Spring-Verlag,1989,113-199.
2.张岩波,等.对数线性模型的最优模型筛选策略.中国卫生统计,1996,13(6)：4., 百拇医药
单位：山西医科大学卫生统计教研室(030001)
关键词：高维列联表；对数线性模型；IPF算法
中国卫生统计990501 【提 要】 目的 采用Newton-Raphson法拟合对数线性模型时，如果列联表的维数太高(≥5)，使得设计矩阵复杂，以及迭代精度等原因，出现病态的信息矩阵，而无法收敛，导致算法失败。本文从应用角度探讨了IPF算法的有效性。方法 采用IPF算法对一个五维表进行了分析。结果 IPF算法能够很好地拟合高维表的模型，并得出了合理的结果。结论 IPF算法简便、稳健，在Newton-Raphson法失效时，不失为处理高维表的解决办法。
IPF Algorithm of Log-linear Model and Software Implement
, http://www.100md.com
Zhang Yanbo ,He Dawei.
Shanxi Medical University (030001),Taiyuan
【Abstract】 Objective When the Newton-Raphson algorithm is used to fit Log-linear model ,if the dimension of a contingency table is too high,it will make the design matrix complicated and present a ill-conditioned information matrix,in addition to the reason of iterative precision,The iteration can not converge and the N-R algorithm is failed.This paper discussed the IPF algorithm in practical aspect.Methods An example of 5-way table was Analyzed using IPF algorithm.Results IPF algorithm could effectively fit the model for high-way table and give a reasonable interpretation.Conclusion For IPF algorithm is simple and robust,it can yet be regarded as a method when the N-R algorithm has been failed.
, 百拇医药
【Key words】 High-way contingency table Log-linear model IPF algorithm
对数线性模型是分析高维列联表的得力工具。出于两种目的，对维数需要进行调整，①为便于解释而降维(减少分析变量)；②进行探索性分析时，在样本含量允许的情况下，希望引入多的变量，以期发现变量间更多的关系。考虑第二种情况，当维数太多时，若算法采用一般认为较优越的Newton-Raphson法(N-R法)其运算速度慢，更甚者，由于交互效应(参数)太多、设计矩阵复杂及迭代精度等原因，导致病态的信息短阵，无法求逆，而难于收敛，使得算法失败；迭代比例拟合算法(IPF算法)有参数估计算法复杂的缺点，但IPF法节省内存、运行速度快，而且求期望值算法简单、稳健，容易得出收敛的结果〔1〕。此时采用IPF法不失为一种解决的办法。本文偏重从应用角度来阐述IPF算法。
原理与方法
, 百拇医药
一、迭代比例拟合算法(Iterative Proportional Fitting Algorithm，IPFA)
IPF算法产生先于N-R法，由Deming和Stephan(1940)导出，后经Bishop(1969)、Haberman(1974)、Meyer(1981)等作过进一步改进，拓广〔1〕。在此以一个三维表的二阶模型为例，简述如何通过IPF算法迭代得出期望值。模型为：
(1)
m表示期望值，以“.”表示合计。由上式可知，各总计mij、mik和mjk受约束等于相应的观察边缘合计。迭代程序假定每个
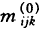的初始值为1，然后按比例调整这些值，以满足第一个边缘约束mij=nij，计算公式为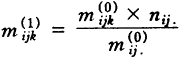：, 百拇医药
(2)
(其中：
)再调整经修正的期望值，以满足另外两个边缘约束，即：mi.k=ni.k、m.jk=n.jk计算公式为：
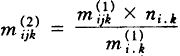
(3)
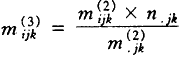
(4)
(其中：
), 百拇医药
至此，第一轮循环结束，将以上各值代入(2)式，开始第二轮循环，直至第t次循环达到收敛标准。即：任一格的第t和第t-1次循环的期望值之差小于某一常量ε。如：
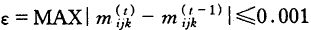，这时可终止迭代。对于一个模型，在模型中有多少个组态(Configuration)，则在每次循环中进行多少次运算。
二、模型的拟合优度检验
1、检验统计量：
(1)似然比统计量G2：G2=2Σyln(y/m)
(2)赤池信息量准则(AIC)：AIC=G2-2DF，便于多个模型拟合效果的比较，AIC越低，拟合效果越好。
, 百拇医药
2、 检验水准：本文采用同步检验过程(Simultaneous Test Procedure)〔2〕，即：γ=1-(1-α)k，k为零效应项数，采用γ的目的在于避免因检验水准选择太高而引进零效应，或检验水准太低而丢失显著的效应项。
3、最优模型筛选，采用Brown′s偏关联检验。
实例分析
例自Sewell与shan对Wisconsin的10 317名高中生是否计划上大学的一项调查，调查变量包括家庭的社会经济地位(socioeconomics status,低/中低/中高/高)、智力水平(Intelligence,低/中下/中上/高)、是否计划入学(Plan college,是/否)、性别(Sex,男/女)和父母重视鼓励程度(parental Encouragement,低/高)。5个变量分别以T、I、P、S、E表示构成4×4×2×2×2的高维表，见表1。
, 百拇医药
表1 高中生入学调查结果 计划入学
(P)
是
否
性 别
(E)
男
女
男
女
父母重视
(S)
高
, http://www.100md.com
低
高
低
高
低
高
低
地位(T)
智力(I)
低
低
4
13
5
, 百拇医药
9
349
64
455
44
中低
9
33
15
14
207
72
312
47
, http://www.100md.com
中高
12
38
8
20
126
54
216
35
高
10
89
13
28
, 百拇医药
67
43
96
24
中低
低
2
27
11
29
232
84
285
61
, 百拇医药
中低
7
64
19
47
201
95
236
88
中高
12
93
12
62
, 百拇医药
115
92
164
85
高
17
119
15
72
79
59
113
50
中高
, 百拇医药
低
8
47
7
36
164
91
163
72
中低
4
74
13
75
, 百拇医药
120
110
193
90
中高
17
148
12
91
92
100
174
100
, 百拇医药 高
6
198
20
142
42
73
81
77
高
低
4
39
16
, 百拇医药
36
48
57
50
58
中低
5
123
5
110
47
90
70
76
, 百拇医药
中高
9
224
13
230
41
65
47
81
高
8
414
13
360
, 百拇医药
17
54
49
98
对表1，采用IPF算法拟合一致阶模型如表2。表2 一致阶模型
模 型
G2
DF
P
检验水准γ
AIC
四维模型[TISP…IPSE
, http://www.100md.com
9.24
9
0.420
0.050
-8.76
三维模型[TIP TIS…PSE]
50.44
42
0.174
0.265
-33.56
二维模型[TI TS TP…SE]
, 百拇医药
138.85
88
0.000
0.560
-37.15
表2可见，模型3的拟合优度显然不能接受，模型2的AIC值较低，说明拟合效果较好，但P<0.265提示可能存在显著的四维交互效应项，因此对模型1，2分别筛选出不同的最优模型为：[PIST EST PE IE]、[PIS PIT IST EST PE IE]。表3为最优模型中各组态的似然比变化(ΔG2)。表3 最优模型各组态似然比变化 模型 1
模型 2
组态
, 百拇医药 ΔG2
DF
P
组态
ΔG2
DF
P
PIST
19.89
9
0.019
PIS
21.68
, 百拇医药
3
0.001
EST
9.95
3
0.019
PIT
19.64
9
0.020
PE
1640.28
1
, 百拇医药
0.000
IST
17.13
9
0.047
IE
145.08
3
0.000
EST
13.34
3
0.004
, 百拇医药
PE
1653.62
1
0.002
IE
144.97
3
0.000
G2=50.99 DF=52
P=0.514 γ=0.471
AIC=-53.01
G2=72.31 DF=64
, 百拇医药
P=0.22 γ=0.487
AIC=-55.69
通过IPF算法对五维表分析，得到了合理的结果。分析结果提示：各变量对入学态度都有不同的影响，其中智力、社会地位、性别与入学态度具有联合作用，父母鼓励重视程度对学生智力及是否入学具有较强的影响。以上两种模型理论上模型1是最佳的，但视实际情况或专业知识，模型2也可选。
利用IPF算法还可进一步借助饱和模型的参数及标准化残差进行分析。小 结
IPF算法计算简便，拟合一个包含R个组态的模型，在每次循环中只进行R次运算，大大节约运算时间，而且可以避免大量复杂的矩阵运算，因此算法稳健。文献报道，IPF算法迭代次数较少，本文实例，一般在10次左右即可达到迭代精度(ε=0.0001)。
对于普通列联表，N-R法和IPF算法往往分析结果一致，N-R法能详细得出参数估计的结果，因此对普通表本文仍提倡使用N-R法。但在进行探索性分析，需处理复杂的高维表时(如维数≥5或更多)，出于迭代精度及设计矩阵复杂的考虑，IPF算法不失为一种解决方法。
, 百拇医药
另外，在分析高维表时，由于变量关系复杂，不妨选择不同模型作为起始模型选出不同的最优模型，结合专业知识作出合理解释。
现行的统计软件中，SAS在CATMOD过程中提供了N-R法，IPF法也可用宏实现；SPSS具备两种算法拟合对数线性模型，特别后者采用IPF法及Brown's偏关联检验筛选最优模型，更是极大地方便了不熟悉模型的科研工作者分析应用。
参考文献
1.Santer T.J,Duffy D.E.The Statistical Analysis of Discrete Data.New York,Spring-Verlag,1989,113-199.
2.张岩波,等.对数线性模型的最优模型筛选策略.中国卫生统计,1996,13(6)：4., 百拇医药