线性回归结合灰色模型在门诊量预测中的应用
作者：王启栋 刘荣甫 刘召平 鞠峰 翟光明
单位：王启栋(济南军区总医院信息科 济南250031)；刘荣甫(济南军区总医院信息科 济南250031)；刘召平(济南军区总医院信息科 济南250031)；鞠峰(济南军区总医院信息科 济南250031)；翟光明(第四军医大学卫生院勤系卫生统计专业)
关键词：线性回归；灰色模型；预测
数理医药学杂志000449
摘 要 应用线性回归技术和GM(1，1)灰色模型对某院1990～1999年门诊量进行了分析预测。结果表明，两种方法的加权组合预测误差较小，能为医院科学决策提供依据，是一种较好的预测方法。
中图分类号： O 242.1 文献标识码： A
, 百拇医药 文章编号：1004-4337(2000)04-0359-02
门诊量是反映医院工作情况的一个重要指标，对其进行统计预测，可以为制定医院的工作计划以及科学决策提供依据。这对于医院加强管理，合理利用现有的卫生资源，减少工作的盲目性，无疑具有重要的现实意义。
1 资料来源及方法
资料来源于某院统计室1990～1999年统计资料汇总表，见表1。
表1 某院1990～1999年门诊量完成情况 年份
1990
1991
1992
1993
, 百拇医药
1994
1995
1996
1997
1998
1999
门诊量(万人)
25.854
28.359
29.346
29.346
29.273
28.858
, 百拇医药
30.100
31.252
31.673
31.840
2 一元线性回归模型的建立
令t=1表示1990年，t=2表示1991年，余者类推。保留1999年数据进行组外回代检验。建立以门诊量YIt为应变量，时间t为自变量的一元线性回归方程，利用第四军医大学卫生统计教研室研制的SPLM软件，在AST486微机上进行数据处理并进行分析预测检验。
① 一般回归方程：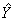
It=26.4077+0.6418t (1)
, 百拇医药
② 方差分析表：见表2。
根据方差分析表得：F=44.9087>F0.01(1,7),P<0.01，因此该回归方程在统计学上有极显著意义。
表2 方差分析表 变异来源
自由度
离均差平方和
均方
F值
P值
总lyy
8
28.5682
, 百拇医药
回归U
1
24.7157
24.7157
44.9087
0.0003
剩余Q
7
3.8525
0.5504
注：n=9 F0.01(1,7)=12.25
③ 应用回归方程(1)进行拟和、预测：
, 百拇医药
具体拟和结果及其残差见表3。表3 某院门诊量线性回归模型拟和结果及其残差 年份
1990
1991
1992
1993
1994
1995
1996
1997
1998
拟和值
27.050
, 百拇医药
27.691
28.333
28.975
29.617
30.259
30.900
31.542
32.184
残 差
-1.196
0.668
1.013
0.298
, 百拇医药
-0.759
-0.159
0.352
0.131
-0.348
残差百分数(%)
-4.6
2.4
3.5
1.0
-2.6
-0.5
1.1
, 百拇医药
0.4
-1.1
剩余标准差S1=0.7419。1999年对应t值等于10，代入方程(1)中得到1999年的预测值为32.826，残差百分数e=(31.840-32.826)/31.840=-3.1%。该残差百分数未超出表3的残差范围。
3 灰色预测模型GM(1，1)[1]
GM(1，1)中括号内第一个1是建模为一阶微分方程，第二个1是预测一个变量。GM(1，1)的建模思路是：用原始数据列y(0)，经生成得到y(1)，对y(1)按GM建模，得生成模型的估计值，将估计值还原就得到原始数据的估计值。
令t=1表示1990年，t=2表示1991年，余者类推。保留1999年数据进行组外回代检验。原始数据列为：Y(0)t={25.854 28.359 29.346 29.346 29.273 28.858 30.100 31.252 31.673}。经过计算，得到灰色预测模型。
, http://www.100md.com
原始数据列的GM(1,1)模型为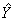：Ⅱt=28.0694×e0.01715(t-1) (2)
具体拟和结果及其残差见表4。
表4 某院门诊量灰色GM(1,1)模型拟和结果及其残差 年份
1990
1991
1992
1993
1994
1995
, 百拇医药
1996
1997
1998
拟和值
25.854
28.311
28.801
29.299
29.806
30.322
30.846
31.380
31.923
, http://www.100md.com
残 差
0
0.048
0.545
0.047
-0.533
-1.464
-0.746
-0.128
-0.25
残差百分数(%)
0
0.17
, 百拇医药
1.86
0.16
-1.82
-5.07
-2.48
0.41
-0.79
剩余标准差S2=0.6579。1999年对应t值等于10，代入方程(2)中得到1999年的预测值为32.754，残差百分数e=(31.840-32.754)/31.840=-2.9%。该残差百分数未超出表4的残差范围。
4 组合预测模型
在给出两种不同预测模型的基础上，利用线性规划[2]的方法来求它们的最优加权组合预测模型。最优加权法的基本原理就是依据某种最优准则构造目标函数Q，在给定约束条件下使Q极小化，以求得组合预测的加权系数。
, 百拇医药
设组合预测模型为：其中a1、a2为待定的加权系数。残差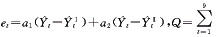
则求得最优非负权重系数的非线性规划模型为：
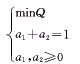(3)
我们通过数学软件Maple中的软件包Simplex进行了(3)式的求解[3]。经过运算，得到如下结果：a1=0.4,a2=0.6，此时目标函数Q达到最小。由此，我们得到最优组合预测模型为：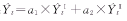
利用该预测模型拟和，得拟作结果及其残差，见表5。
表5 某院门诊量组合预测模型拟和结果及其残差 年份
, http://www.100md.com 1990
1991
1992
1993
1994
1995
1996
1997
1998
拟和值
26.332
28.863
28.613
, 百拇医药
29.169
29.730
30.297
30.867
31.445
32.027
残 差
-0.478
-0.504
0.733
0.177
-0.457
-1.439
, http://www.100md.com
-0.767
-0.193
-0.354
残差百分数(%)
-1.8
-1.8
2.5
0.6
-1.6
-5.0
-2.5
-0.6
-1.1
, 百拇医药
剩余标准差S=0.600。1999年的预测值为32.782，残差百分数e=(31.840-32.782)/31.840=-2.9%。该残差百分数也未超出表4的残差范围。
5 讨论
5.1 本方法具有较好的理论支持，虽然计算复杂，工作量大，但在计算机已经普及的今天，计算时间是以秒计的。在实际工作中应用是可行的，具有一定的现实意义。笔者将其用于我院门诊量、出院人数等的预测，均得到了较理想结果。
5.2 由于影响医院门诊的因素太多，且变化较大，因此采用本法进行远期外推预测时要慎重考虑。统计预测是一门年轻的学科，它综合了统计学、高等数学、计算机科学等相关学科，在科学管理日益重要的今天，它在医院管理中的作用会愈来愈重要。因此，对它进行深入的理论研究和实际应用具有重要的现实意义。
参 考 文 献
1，邓聚龙著.灰色预测与决策.武汉：华中理工大学出版社，1996，125～130.
2，吴立煦，朱幼文译.运筹学.上海：上海人民出版社，1987.
3，范红兵编著.计算机数学实验技术.济南：山东大学数学与系统科学学院，1997.
收稿日期：2000-01-30, 百拇医药
单位：王启栋(济南军区总医院信息科 济南250031)；刘荣甫(济南军区总医院信息科 济南250031)；刘召平(济南军区总医院信息科 济南250031)；鞠峰(济南军区总医院信息科 济南250031)；翟光明(第四军医大学卫生院勤系卫生统计专业)
关键词：线性回归；灰色模型；预测
数理医药学杂志000449
摘 要 应用线性回归技术和GM(1，1)灰色模型对某院1990～1999年门诊量进行了分析预测。结果表明，两种方法的加权组合预测误差较小，能为医院科学决策提供依据，是一种较好的预测方法。
中图分类号： O 242.1 文献标识码： A
, 百拇医药 文章编号：1004-4337(2000)04-0359-02
门诊量是反映医院工作情况的一个重要指标，对其进行统计预测，可以为制定医院的工作计划以及科学决策提供依据。这对于医院加强管理，合理利用现有的卫生资源，减少工作的盲目性，无疑具有重要的现实意义。
1 资料来源及方法
资料来源于某院统计室1990～1999年统计资料汇总表，见表1。
表1 某院1990～1999年门诊量完成情况 年份
1990
1991
1992
1993
, 百拇医药
1994
1995
1996
1997
1998
1999
门诊量(万人)
25.854
28.359
29.346
29.346
29.273
28.858
, 百拇医药
30.100
31.252
31.673
31.840
2 一元线性回归模型的建立
令t=1表示1990年，t=2表示1991年，余者类推。保留1999年数据进行组外回代检验。建立以门诊量YIt为应变量，时间t为自变量的一元线性回归方程，利用第四军医大学卫生统计教研室研制的SPLM软件，在AST486微机上进行数据处理并进行分析预测检验。
① 一般回归方程：
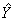It=26.4077+0.6418t (1), 百拇医药
② 方差分析表：见表2。
根据方差分析表得：F=44.9087>F0.01(1,7),P<0.01，因此该回归方程在统计学上有极显著意义。
表2 方差分析表 变异来源
自由度
离均差平方和
均方
F值
P值
总lyy
8
28.5682
, 百拇医药
回归U
1
24.7157
24.7157
44.9087
0.0003
剩余Q
7
3.8525
0.5504
注：n=9 F0.01(1,7)=12.25
③ 应用回归方程(1)进行拟和、预测：
, 百拇医药
具体拟和结果及其残差见表3。表3 某院门诊量线性回归模型拟和结果及其残差 年份
1990
1991
1992
1993
1994
1995
1996
1997
1998
拟和值
27.050
, 百拇医药
27.691
28.333
28.975
29.617
30.259
30.900
31.542
32.184
残 差
-1.196
0.668
1.013
0.298
, 百拇医药
-0.759
-0.159
0.352
0.131
-0.348
残差百分数(%)
-4.6
2.4
3.5
1.0
-2.6
-0.5
1.1
, 百拇医药
0.4
-1.1
剩余标准差S1=0.7419。1999年对应t值等于10，代入方程(1)中得到1999年的预测值为32.826，残差百分数e=(31.840-32.826)/31.840=-3.1%。该残差百分数未超出表3的残差范围。
3 灰色预测模型GM(1，1)[1]
GM(1，1)中括号内第一个1是建模为一阶微分方程，第二个1是预测一个变量。GM(1，1)的建模思路是：用原始数据列y(0)，经生成得到y(1)，对y(1)按GM建模，得生成模型的估计值，将估计值还原就得到原始数据的估计值。
令t=1表示1990年，t=2表示1991年，余者类推。保留1999年数据进行组外回代检验。原始数据列为：Y(0)t={25.854 28.359 29.346 29.346 29.273 28.858 30.100 31.252 31.673}。经过计算，得到灰色预测模型。
, http://www.100md.com
原始数据列的GM(1,1)模型为：
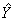Ⅱt=28.0694×e0.01715(t-1) (2)具体拟和结果及其残差见表4。
表4 某院门诊量灰色GM(1,1)模型拟和结果及其残差 年份
1990
1991
1992
1993
1994
1995
, 百拇医药
1996
1997
1998
拟和值
25.854
28.311
28.801
29.299
29.806
30.322
30.846
31.380
31.923
, http://www.100md.com
残 差
0
0.048
0.545
0.047
-0.533
-1.464
-0.746
-0.128
-0.25
残差百分数(%)
0
0.17
, 百拇医药
1.86
0.16
-1.82
-5.07
-2.48
0.41
-0.79
剩余标准差S2=0.6579。1999年对应t值等于10，代入方程(2)中得到1999年的预测值为32.754，残差百分数e=(31.840-32.754)/31.840=-2.9%。该残差百分数未超出表4的残差范围。
4 组合预测模型
在给出两种不同预测模型的基础上，利用线性规划[2]的方法来求它们的最优加权组合预测模型。最优加权法的基本原理就是依据某种最优准则构造目标函数Q，在给定约束条件下使Q极小化，以求得组合预测的加权系数。
, 百拇医药
设组合预测模型为：其中a1、a2为待定的加权系数。残差
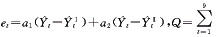则求得最优非负权重系数的非线性规划模型为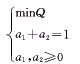： (3)我们通过数学软件Maple中的软件包Simplex进行了(3)式的求解[3]。经过运算，得到如下结果：a1=0.4,a2=0.6，此时目标函数Q达到最小。由此，我们得到最优组合预测模型为：
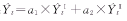利用该预测模型拟和，得拟作结果及其残差，见表5。表5 某院门诊量组合预测模型拟和结果及其残差 年份
, http://www.100md.com 1990
1991
1992
1993
1994
1995
1996
1997
1998
拟和值
26.332
28.863
28.613
, 百拇医药
29.169
29.730
30.297
30.867
31.445
32.027
残 差
-0.478
-0.504
0.733
0.177
-0.457
-1.439
, http://www.100md.com
-0.767
-0.193
-0.354
残差百分数(%)
-1.8
-1.8
2.5
0.6
-1.6
-5.0
-2.5
-0.6
-1.1
, 百拇医药
剩余标准差S=0.600。1999年的预测值为32.782，残差百分数e=(31.840-32.782)/31.840=-2.9%。该残差百分数也未超出表4的残差范围。
5 讨论
5.1 本方法具有较好的理论支持，虽然计算复杂，工作量大，但在计算机已经普及的今天，计算时间是以秒计的。在实际工作中应用是可行的，具有一定的现实意义。笔者将其用于我院门诊量、出院人数等的预测，均得到了较理想结果。
5.2 由于影响医院门诊的因素太多，且变化较大，因此采用本法进行远期外推预测时要慎重考虑。统计预测是一门年轻的学科，它综合了统计学、高等数学、计算机科学等相关学科，在科学管理日益重要的今天，它在医院管理中的作用会愈来愈重要。因此，对它进行深入的理论研究和实际应用具有重要的现实意义。
参 考 文 献
1，邓聚龙著.灰色预测与决策.武汉：华中理工大学出版社，1996，125～130.
2，吴立煦，朱幼文译.运筹学.上海：上海人民出版社，1987.
3，范红兵编著.计算机数学实验技术.济南：山东大学数学与系统科学学院，1997.
收稿日期：2000-01-30, 百拇医药