固体药物制剂体外溶出过程数学模型在中药丸剂中的应用
作者：韩永平 向永臣
单位：成都中医药大学 药学院，四川 成都 610075
关键词：固体制剂；溶出；数学模型
成都中医药大学学报000226摘 要：运用物质传递的基本原理，通过对固体制剂的体外溶出过程进行较为深入的理论分析，建立了相应的宏观动力学数学模型。将其实际应用于中药香连丸释放度数据的考察，不仅确定了不同样品该过程的速度控制步骤，为药物制剂工艺的优化提供了理论依据，而且也对模型的合理性进行了验证。
中图分类号：R944.2；R954 文献标识码：A 文章编号：1004-0668(2000)02-0048-03
作者简介：韩永平，男，1965年2月生；博士后研究人员，副教授，硕士生导师；研究方向：制药工程。
, 百拇医药
固体药物制剂体外溶出度的测定是考察固体制剂处方组成、辅料及生产工艺等因素对制剂质量影响的基本方法。其过程主要包括固体制剂的崩解和有效成分溶出两个步骤。通过测定不同时刻有效成分的溶出量，可以预估药物在体内的吸收效果，评价制剂的质量。
关于西药固体制剂的体外溶出过程，已有一些数学模型加以描述[1]。其中多数为经验模型，而根据Fick定律推导出的Higuchi方程[2]，虽为理论研究打下了基础，但却无法判断过程的机制。而中药固体制剂体外溶出过程则远未达到模型化水平。我们在对该过程提出合理分析、假设的基础上，运用物质传递理论，建立了新的数学模型，并实际应用于不同厂家生产的香连丸溶出数据的分析，取得了令人满意的结果。现讨论如下。
1 宏观动力学模型的推导
1.1 溶出过程的基本分析
, 百拇医药 在固体药物制剂的体外溶出过程中，首先发生崩解作用，产生大量微小的药物颗粒；然后药物小颗粒在一定介质中不断溶解，有效成分逐渐溶出。药物小颗粒在介质的作用下不断缩小，直至完全消失。当崩解速度远大于有效成分的溶出速度时，可忽略崩解对过程速率的影响。本文对此条件下过程的宏观动力学数学模型进行了研究。
假设药物的溶出过程按下述步骤进行：(1)溶剂分子A由液相主体通过固体表面液膜传递至固体表面。(2)在固体表面，溶剂A与固体中有效成分B进行溶剂化反应(包括水合反应、酸解反应或碱解反应等)。(3)液体产物F(包括B的水合物、酸解产物或碱解产物等)由固体表面通过液膜传递至液相主体。
由于步骤(3)较少控制过程速率，因此只讨论步骤(1)和(2)分别为控速步骤时的宏观动力学模型。为简化推导过程，提出下两项假设：第一，溶解过程是拟稳定过程，即溶剂A的传递速率等于其在反应中消耗的速率，液固相界面处无物质积累；第二，颗粒内部各处温度均匀。综上所述，体外溶出过程应视为广义的反应过程和传质过程的串联，总反应式可表示为
, 百拇医药
A(l)+bB(s)→fF(l) ①
1.2 当过程速率受溶剂A的液膜扩散控制时
此时化学反应步骤速度较快，因此溶剂A在颗粒表面浓度可视为零。设颗粒初始率径为RS，到时间τ时缩小为RC。
与Nernst-Noyes-Whitney方程[3]类似，液体溶剂A通过液膜的扩散传递速率为：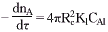
②
式中，Kl为A的外扩散传质系数，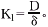
D为扩散系数，δ为液膜厚度；CAl为溶剂A在液相主体中的摩尔浓度(mol。 L-1)。
, 百拇医药
根据球形颗粒的几何特性，在单位时间单个颗粒内反应物B的反应速率为：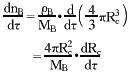
③
式中，ρ B，MB分别为固体成分B的密度和摩尔质量(g/mol)，其中，kl是颗粒半径RC的函数，由资料[4]可得其经验表达式：
当搅拌较慢时，考虑液体在滞流状况下；上式可变为：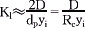
④
式中，dp为颗粒粒径；D为溶剂A的扩散系数；yi为惰性组分在扩散膜两侧的平均摩尔分率。
, 百拇医药
由式①的化学计量关系，可得：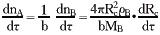
⑤
由②、④、⑤式，得：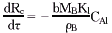
假定在溶解过程中溶剂A的浓度CAl变化较小，可视为常数，将上式积分，可得：
而药物颗粒完全溶解时间为：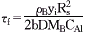
时间分率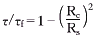
⑥
, 百拇医药
定义固体成分B的反应率xB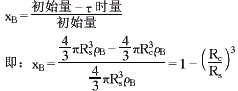
将xB代入式⑥，得：τ/τf＝1-(1-xB)2/3 ⑦
上式即为如溶剂A的液膜扩散步骤为溶出过程控速步骤时的数学模型。
1.3 当药物溶出过程受固体表面反应控制时
根据化学反应动力学理论，假定为一级反应，则溶剂A在固体表面与B的化学反应速率为：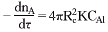
式中，k为表面反应速率常数
, 百拇医药
将式⑤代入，得：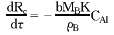
积分，得：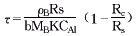
药物完全溶出时间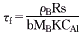
则时间分率：
τ/τf＝1-(1-xB)1/3
上式即为表面化学反应步骤为溶出过程控制步骤时的数学模型。
1.4 药物溶出过程控制步骤的判别
, 百拇医药
基于推导出的不同控制步骤下的数学模型，我们可以从药物有效成分的累积释放度与溶解时间的关系，对过程的控制步骤加以判别，由此可对药物制剂的研究提供理论依据。
虽然本文所提模型的假设条件很少，但由于固体制的溶出过程受到崩解速度、辅料品种、用量及颗粒表面形态等诸因素影响，在使用时必须根据具体情况加以分析。
3 模型应用实例
我们应用模型对中成药香连丸有效成分的累积释放度随时间变化的数据进行了剖析。文献[5]对国内两家生产香莲丸的药厂生产的5批香连丸的体外溶出度进行了测定。我们在此基础上用模型加以拟合。其数据处理过程如下。
(1)由各时刻的有效成分累积释放度测定值，求取模型参数值(τf值，再由各时刻的If值计算算术平均值，作为选定值。(2)由选定的模型参数(τf值计算出相应时刻的累积释放率，并以测定的标准计算相对误差，考察拟合结果。数据处理结果见表1～表5。
, 百拇医药
表1 A厂第一号样品实验值与模型计算值比较 时间
(min)
累积释放率(%)
相对误差
(%)
选用模型
模型参数
(τf)
实验值
计算值
10
15.20
, 百拇医药
15.20
0
反应模型
扩
散
模
型
187.00
339.11
表2 A厂第二号样品实验值与模型计算值比较 时间
(min)
累积释放率(%)
相对误差
, http://www.100md.com
(%)
选用模型
模型参数
(τf)
实验值
计算值
10
15.84
15.84
0
反应模型
扩
散
, http://www.100md.com
模
型
179.01
628.39
表3 A厂第三号样品实验值与模型计算值比较 时间
(min)
累积释放率(%)
相对误差
(%)
选用模型
模型参数
(τf)
, 百拇医药
实验值
计算值
10
14.47
14.47
0
反应模型
扩
散
模
型
表4 B厂第一号样品实验值与模型计算值比较 时间
(min)
, http://www.100md.com
累积释放率(%)
相对误差
(%)
选用模型
模型参数
(τf)
实验值
计算值
10
20.29
20.96
3.30
化
, 百拇医药
学
反
应
模
型
132.57
表5 B厂第二号样品实验值与模型计算值比较 时间
(min)
累积释放率(%)
相对误差
(%)
选用模型
模型参数
, 百拇医药
(τf)
实验值
计算值
10
24.67
21.03
14.75
化
学
反
应
模
型
, http://www.100md.com
132.10
从表1～表5可知,数据拟合效果较好,数学模型计算值基本反映了实测数据的变化趋势。其中A厂的3批产品体外溶出过程基本符合液膜扩散模型。由于在溶初期液相主体中指标成分浓度很低，扩散传质推动力很大，传质阻力很小，过程速度率应受颗粒表面水合反应(即化学反应)控制，因此在表1～3中对A厂3批样品的溶出度数据进行分段拟合，即对溶出初期(前10分钟)的数据以化学反应模型进行拟合，然后以第10分钟为起点，以此时的累积释放率为基准，用液膜扩散模型拟合后的数据，而B厂的两批产品则在整个溶出过程中基本符合化学反应模型。以上模型计算结果表明，A厂产品的溶出过程主要受液膜扩散步骤；B厂产品则主要受化学反应步骤控制，说明A厂还可进一步改进生产工艺，降低扩散阻力，以加快整个溶出过程的进行，B厂产品则已基本达到了这样的要求。这一结论从模型参数τf的值也可看出。
3 讨论
通过对固体药物制剂体外溶出过程的剖析，基于不同的控速步骤，分别建立了以下宏观动力学模型：
, 百拇医药
过程速率受溶剂A的液膜扩散控制时，下式成立：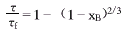
(2)过程速率受固体颗粒表面化学及应控制时，下式成立：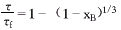
此外，我们还通过对实测数据的模型计算，不仅验证了模型的合理性，而且也从理论的角度指明了工艺改革的方向。
参考文献
1 奚念朱.药剂学[M].第三版.北京：人民卫生出版社，1996.454～457
2 Higuchi T. Mechanism of sustained-action medication, theoertical analysis of rate of release of solid drugs disperesd in solid matrices[J].J Pharm Sc.,1963,52:115
3 奚念朱.药剂学[M].第三版.北京：人民卫生出版社，1996.257～258
4 天津大学编.化工传递过程[M].北京：化学工业出版社，1980.284～286
5 辛勋，刘萍.香连丸溶出度的研究[J].中成药，1991，13(11)：2
(收稿日期：1999-07-15)
, http://www.100md.com
单位：成都中医药大学 药学院，四川 成都 610075
关键词：固体制剂；溶出；数学模型
成都中医药大学学报000226摘 要：运用物质传递的基本原理，通过对固体制剂的体外溶出过程进行较为深入的理论分析，建立了相应的宏观动力学数学模型。将其实际应用于中药香连丸释放度数据的考察，不仅确定了不同样品该过程的速度控制步骤，为药物制剂工艺的优化提供了理论依据，而且也对模型的合理性进行了验证。
中图分类号：R944.2；R954 文献标识码：A 文章编号：1004-0668(2000)02-0048-03
作者简介：韩永平，男，1965年2月生；博士后研究人员，副教授，硕士生导师；研究方向：制药工程。
, 百拇医药
固体药物制剂体外溶出度的测定是考察固体制剂处方组成、辅料及生产工艺等因素对制剂质量影响的基本方法。其过程主要包括固体制剂的崩解和有效成分溶出两个步骤。通过测定不同时刻有效成分的溶出量，可以预估药物在体内的吸收效果，评价制剂的质量。
关于西药固体制剂的体外溶出过程，已有一些数学模型加以描述[1]。其中多数为经验模型，而根据Fick定律推导出的Higuchi方程[2]，虽为理论研究打下了基础，但却无法判断过程的机制。而中药固体制剂体外溶出过程则远未达到模型化水平。我们在对该过程提出合理分析、假设的基础上，运用物质传递理论，建立了新的数学模型，并实际应用于不同厂家生产的香连丸溶出数据的分析，取得了令人满意的结果。现讨论如下。
1 宏观动力学模型的推导
1.1 溶出过程的基本分析
, 百拇医药 在固体药物制剂的体外溶出过程中，首先发生崩解作用，产生大量微小的药物颗粒；然后药物小颗粒在一定介质中不断溶解，有效成分逐渐溶出。药物小颗粒在介质的作用下不断缩小，直至完全消失。当崩解速度远大于有效成分的溶出速度时，可忽略崩解对过程速率的影响。本文对此条件下过程的宏观动力学数学模型进行了研究。
假设药物的溶出过程按下述步骤进行：(1)溶剂分子A由液相主体通过固体表面液膜传递至固体表面。(2)在固体表面，溶剂A与固体中有效成分B进行溶剂化反应(包括水合反应、酸解反应或碱解反应等)。(3)液体产物F(包括B的水合物、酸解产物或碱解产物等)由固体表面通过液膜传递至液相主体。
由于步骤(3)较少控制过程速率，因此只讨论步骤(1)和(2)分别为控速步骤时的宏观动力学模型。为简化推导过程，提出下两项假设：第一，溶解过程是拟稳定过程，即溶剂A的传递速率等于其在反应中消耗的速率，液固相界面处无物质积累；第二，颗粒内部各处温度均匀。综上所述，体外溶出过程应视为广义的反应过程和传质过程的串联，总反应式可表示为
, 百拇医药
A(l)+bB(s)→fF(l) ①
1.2 当过程速率受溶剂A的液膜扩散控制时
此时化学反应步骤速度较快，因此溶剂A在颗粒表面浓度可视为零。设颗粒初始率径为RS，到时间τ时缩小为RC。
与Nernst-Noyes-Whitney方程[3]类似，液体溶剂A通过液膜的扩散传递速率为：
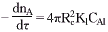②式中，Kl为A的外扩散传质系数，
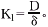D为扩散系数，δ为液膜厚度；CAl为溶剂A在液相主体中的摩尔浓度(mol。 L-1)。, 百拇医药
根据球形颗粒的几何特性，在单位时间单个颗粒内反应物B的反应速率为：
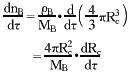③式中，ρ B，MB分别为固体成分B的密度和摩尔质量(g/mol)，其中，kl是颗粒半径RC的函数，由资料[4]可得其经验表达式：
当搅拌较慢时，考虑液体在滞流状况下；上式可变为：
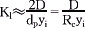④式中，dp为颗粒粒径；D为溶剂A的扩散系数；yi为惰性组分在扩散膜两侧的平均摩尔分率。
, 百拇医药
由式①的化学计量关系，可得：
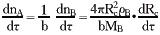⑤由②、④、⑤式，得：
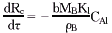
假定在溶解过程中溶剂A的浓度CAl变化较小，可视为常数，将上式积分，可得：
而药物颗粒完全溶解时间为：
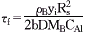
时间分率
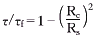⑥, 百拇医药
定义固体成分B的反应率xB
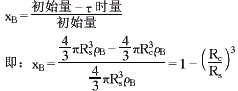
将xB代入式⑥，得：τ/τf＝1-(1-xB)2/3 ⑦
上式即为如溶剂A的液膜扩散步骤为溶出过程控速步骤时的数学模型。
1.3 当药物溶出过程受固体表面反应控制时
根据化学反应动力学理论，假定为一级反应，则溶剂A在固体表面与B的化学反应速率为：
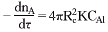
式中，k为表面反应速率常数
, 百拇医药
将式⑤代入，得：
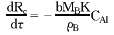
积分，得：
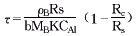
药物完全溶出时间
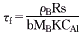
则时间分率：
τ/τf＝1-(1-xB)1/3
上式即为表面化学反应步骤为溶出过程控制步骤时的数学模型。
1.4 药物溶出过程控制步骤的判别
, 百拇医药
基于推导出的不同控制步骤下的数学模型，我们可以从药物有效成分的累积释放度与溶解时间的关系，对过程的控制步骤加以判别，由此可对药物制剂的研究提供理论依据。
虽然本文所提模型的假设条件很少，但由于固体制的溶出过程受到崩解速度、辅料品种、用量及颗粒表面形态等诸因素影响，在使用时必须根据具体情况加以分析。
3 模型应用实例
我们应用模型对中成药香连丸有效成分的累积释放度随时间变化的数据进行了剖析。文献[5]对国内两家生产香莲丸的药厂生产的5批香连丸的体外溶出度进行了测定。我们在此基础上用模型加以拟合。其数据处理过程如下。
(1)由各时刻的有效成分累积释放度测定值，求取模型参数值(τf值，再由各时刻的If值计算算术平均值，作为选定值。(2)由选定的模型参数(τf值计算出相应时刻的累积释放率，并以测定的标准计算相对误差，考察拟合结果。数据处理结果见表1～表5。
, 百拇医药
表1 A厂第一号样品实验值与模型计算值比较 时间
(min)
累积释放率(%)
相对误差
(%)
选用模型
模型参数
(τf)
实验值
计算值
10
15.20
, 百拇医药
15.20
0
反应模型
扩
散
模
型
187.00
339.11
表2 A厂第二号样品实验值与模型计算值比较 时间
(min)
累积释放率(%)
相对误差
, http://www.100md.com
(%)
选用模型
模型参数
(τf)
实验值
计算值
10
15.84
15.84
0
反应模型
扩
散
, http://www.100md.com
模
型
179.01
628.39
表3 A厂第三号样品实验值与模型计算值比较 时间
(min)
累积释放率(%)
相对误差
(%)
选用模型
模型参数
(τf)
, 百拇医药
实验值
计算值
10
14.47
14.47
0
反应模型
扩
散
模
型
表4 B厂第一号样品实验值与模型计算值比较 时间
(min)
, http://www.100md.com
累积释放率(%)
相对误差
(%)
选用模型
模型参数
(τf)
实验值
计算值
10
20.29
20.96
3.30
化
, 百拇医药
学
反
应
模
型
132.57
表5 B厂第二号样品实验值与模型计算值比较 时间
(min)
累积释放率(%)
相对误差
(%)
选用模型
模型参数
, 百拇医药
(τf)
实验值
计算值
10
24.67
21.03
14.75
化
学
反
应
模
型
, http://www.100md.com
132.10
从表1～表5可知,数据拟合效果较好,数学模型计算值基本反映了实测数据的变化趋势。其中A厂的3批产品体外溶出过程基本符合液膜扩散模型。由于在溶初期液相主体中指标成分浓度很低，扩散传质推动力很大，传质阻力很小，过程速度率应受颗粒表面水合反应(即化学反应)控制，因此在表1～3中对A厂3批样品的溶出度数据进行分段拟合，即对溶出初期(前10分钟)的数据以化学反应模型进行拟合，然后以第10分钟为起点，以此时的累积释放率为基准，用液膜扩散模型拟合后的数据，而B厂的两批产品则在整个溶出过程中基本符合化学反应模型。以上模型计算结果表明，A厂产品的溶出过程主要受液膜扩散步骤；B厂产品则主要受化学反应步骤控制，说明A厂还可进一步改进生产工艺，降低扩散阻力，以加快整个溶出过程的进行，B厂产品则已基本达到了这样的要求。这一结论从模型参数τf的值也可看出。
3 讨论
通过对固体药物制剂体外溶出过程的剖析，基于不同的控速步骤，分别建立了以下宏观动力学模型：
, 百拇医药
过程速率受溶剂A的液膜扩散控制时，下式成立：
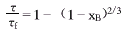
(2)过程速率受固体颗粒表面化学及应控制时，下式成立：
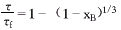
此外，我们还通过对实测数据的模型计算，不仅验证了模型的合理性，而且也从理论的角度指明了工艺改革的方向。
参考文献
1 奚念朱.药剂学[M].第三版.北京：人民卫生出版社，1996.454～457
2 Higuchi T. Mechanism of sustained-action medication, theoertical analysis of rate of release of solid drugs disperesd in solid matrices[J].J Pharm Sc.,1963,52:115
3 奚念朱.药剂学[M].第三版.北京：人民卫生出版社，1996.257～258
4 天津大学编.化工传递过程[M].北京：化学工业出版社，1980.284～286
5 辛勋，刘萍.香连丸溶出度的研究[J].中成药，1991，13(11)：2
(收稿日期：1999-07-15)
, http://www.100md.com