多元非线性回归参数估计的数论方法及应用*
作者：孙晓武 方积乾 杨杏芬
单位：孙晓武 方积乾 中山医科大学卫生统计学教研室(510089)； 杨杏芬 中山医科大学卫生毒理学教研室
关键词：多元非线性回归；数论方法；二硫化碳
中国卫生统计990102 【提 要】 目的 构造多元非线性回归模型，分析职业流行病学研究中职业暴露的多个效应。方法 应用数论方法解决模型的参数估计问题。结果 在二硫化碳对工人的健康评价中，建立了二元非线性回归方程，数论方法所得参数估计的标准误小于SASProc NLIN一元回归结果。结论 数论方法为多元非线性模型提供了简便易行的参数估计手段。
Number-theoretic Method for Parameters Estimation in Multivariate Nonlinear Regression with Application
, 百拇医药
Sun Xiaowu,Fang Jiqian,Department of Health Statistics,Sun Yet-Sen University of Medical Science (510089),Guangzhou
【Abstract】 Objective Developing multivariate nonlinear regression models to characterize the effect of occupational exposure in occupational epidemiology.Methods Number-theoretic(NT)method was used to estimate parametes in model.Results In the evaluation of health effects of CS2,two-outcome nonlinear model was develped,and the standard errors of estimated parameters from NT-method were smaller than those from SAS Proc NLIN.Conclusion NT method provides a simple and easy way to the estimation for multivariate nonlinear models.
, http://www.100md.com
【Key words】 Multivariate nonlinear regression Number-theoretic method CS2
引言
职业流行病学研究中常用多个指标刻划职业暴露的效应。如杨杏芬等〔1〕研究了某化纤厂工人尿中高香草酸(HVA)和香草扁桃酸(VMA)与接触二硫化碳的关系。HVA和VMA作为多巴胺代谢终产物可以提示CS2对神经化学代谢的干扰作用。为探讨这两种产物与CS2之间的暴露效应关系，需分别建立回归方程。实际上由于各指标间的相关性，我们应综合起来分析，以提供更加精确的参数估计，并确定更加符合实际的模型。对多元非线性回归模型，Bates和Watts的专著〔2〕中给出参数估计和假设检验方法，但现有统计软件未能提供相应的处理，且按他们的方法编程也复杂。本文在第二节介绍了非线性回归方法，然后应用方开泰和王元〔3〕提出的数论方法解决有关的统计推断问题；第三节通过实例分析演示方法的应用；最后讨论了方法中的有关问题。
, http://www.100md.com
模型和数论方法
1.模型与参数统计推断
设样本含量为N，每个人有M个响应变量，共依赖于p个参数β，建立多元非线性回归方程
Yn=f(xn,β)+en, n=1,…，N；
(1)
其中随机向量Yn=(Yn1,Yn2,…，YnM)对应于第n个人响应变量的观测值；f=(f1,f2,…,fM)，,fm(.，β)是第m个响应变量的模型函数，依赖于自变量Xn及参数β，En=(en1,en2,…，enM)为随机误差项。设E1，E2，…，EN相互独立且服从多元正态分布Np(0,Σ)，则有关于参数的似然函数：
, 百拇医药
(2)
。上式对Σ-1求偏导并令为零，得到
(3)
代入(2)式得条件对数似然函数
(4)
从而β的极大似然估计可通过对|ETE|关于β求解极小值得到，此即多元响应模型的行列式准则。显然，这是一元响应最小二乘准则的推广。
H为对数似然函数关于β的二阶偏导阵，则H-1作为
的协方差矩阵的估计
θ。的1-α置信域为下式所包围的β的区域(为β的极大似然估计)
, 百拇医药
(5)
这个区域虽较精确，但必须通过数值方法来确定。参数βp的1-α置信区间由下式近似得到：
(6)
2.参数估计的数论方法
现有的软件可作参数一般非线性最小二乘估计。对于多元响应行列式准则下的参数估计，Bates和Watts〔2〕给出推广的高斯-牛顿法，但目前常用的软件尚未实现。方法涉及对行列式求参数二阶偏导数，公式复杂，编程繁杂。我们这里采用方开泰和王元〔3〕提出的序贯优化数论方法(Sequential number-theoretic optimization,SNTO)求解。步骤如下：
, http://www.100md.com
步骤0：令t=0，确定初始搜索范围：p维矩形D0=〔a10，b10〕×〔a20，b20〕×…×〔ap0，bp0〕，其中ai0=βi0-ci0,bi0=βi0+ci0。βi0是βi的初始估计。
步骤1：用某一数论方法产生nt个点的点集Θt使其在Dt上均匀分布。
, 百拇医药
步骤2：对每个β∈β0UBt，按式(4)计算似然函数；求βt使得
(7)
步骤3：停止准则：若最大的两个L(β，(β))值差距小于预先给定的δ，则停止搜索；否则进入下一步。
步骤4：收缩区域：定义新的区域
(γ为预先指定的收缩比值)，
；返回步骤1。
3.协方差阵估计
, 百拇医药
H为对数似然函数关于β的二阶偏导阵，则H-1作为的协方差阵的估计。将似然函数在处作二阶泰勒展开，忽略高阶项则有
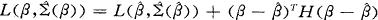
(8)
我们在的邻域内选择k(>p(p+1)/2)个点，计算对应的似然函数值，再拟合(8)式，即得
。在勒康和罗昭容〔4〕的专著中给出类似的算法。
应 用
, 百拇医药
杨杏芬等〔1〕研究了60名某化纤厂接触二硫化碳工人和48名对照组人员尿中高香草酸(HVA)和香草扁桃酸(VMA)这两种多巴胺代谢产物的变化规律。初步分析结果表明，HVA和VMA与环境CS2暴露浓度呈负相关，并符合负指数变化规律。下面的分析基于下述多元非线性回归方程：
ENVC表示环境CS2浓度。
一元非线性回归在SAS上实现，并作为多元回归估计的初始估计。按文献〔3〕提供的好格子点(good lattice point,GLP)集合表，选择生成矢量(307；1，42，229，101)，采用SNTO法经过两次循环即满足收敛要求，结果见表1。
表1 一元与多元非线性回归结果对比
, 百拇医药
一元(Proc NLIN)
多元(NT)
SE()
SE()
HVA
a1
2.1565
0.0686
, 百拇医药
2.1641
0.0678
b1
-0.0063*
0.0017
-0.0063*
0.0016
VMA
a2
1.1641
0.0429
1.4057
, 百拇医药
0.0426
b2
-0.0024
0.0015
-0.0029*
0.0014
*P<0.05 多元回归的参数标准误都较一元回归相应的要小。结果提示接触者导致HVA和VMA降低，该结果与以前文献报道的动物实验发现CS2干扰神经化学代谢的结果具有一致性。
讨 论
1.实际应用中评价某有害暴露会有多个指标，这些指标一般都是相关的，理应综合起来分析，以提供更加精确的参数估计，并确定更加符合实际的模型。但过去限于理论和计算手段只能分开来考虑各指标与暴露和其他影响因素的关系。本文尝试用数论方法来解决多元非线性回归的参数估计问题，经实例验证较单个响应变量的分析精度高。
, http://www.100md.com
2.自70年代末方开泰和王元应用数论方法提出“均匀设计”以来，数论方法在统计领域有了广泛的应用〔3〕。用数论方法解决统计中的优化问题有三个优点：第一，对目标函数只有连续性要求，对多峰或不连续的(如最小一乘法)目标函数仍然有效。第二，不必计算各阶微商，编制计算程序异常方便。本文的结果是用SAS/IML编写少量的语句完成计算的。但确定适当的搜索区域和选择合适足够的格子点数非常重要，这需要对资料和背景知识有充分的认识。第三，不依赖于初始值的选取。
3.一般而言，采用多元回归模型其参数的标准误估计要小于一元模型，但本文采用的协方差近似估计在只有O(N-1)阶精度。为此，或者对似然函数作更高阶近似，或探讨Bootstrap法的应用，或采用基于Bayes原理的Gibbs抽样方法，将有望提高多元响应时的协方差估计可靠性。另外，在某些参数的显著性不高或有多余的参数时，本文提出的估计协方差的方法会失效。变量筛选和数论方法如何结合是个值得研究的问题。
, http://www.100md.com
4.本文的实例分析是最简单的例子，我们今后将在复杂模型的评价、随机效应的处理及其他感兴趣的方面作有益的探索。
*本文受中华医学基金会(CMB)资助
参考文献
1.杨杏芬，等.接触二硫化碳工人尿中高香草酸和香草扁桃酸的变化.环境与职业医学论文集(1)，广州：中山医科大学环境与职业医学中心，1995；121
2.Bates DM and Watts DG.Nonlinear Regression Analysis and its Applications.New York:John Wiley & Sons,1988
3.方开泰，王元.数论方法在统计中的应用.北京：科学出版社，1994
4.韦博成.近代非线性回归分析.南京：东南大学出版社，1989
5.勒康，罗昭容.统计渐近论基础.北京：科学出版社，1993
6.SAS Inc.SAS/IML User's Guide,version 6,Cary:SAS Inc.,1992, http://www.100md.com
单位：孙晓武 方积乾 中山医科大学卫生统计学教研室(510089)； 杨杏芬 中山医科大学卫生毒理学教研室
关键词：多元非线性回归；数论方法；二硫化碳
中国卫生统计990102 【提 要】 目的 构造多元非线性回归模型，分析职业流行病学研究中职业暴露的多个效应。方法 应用数论方法解决模型的参数估计问题。结果 在二硫化碳对工人的健康评价中，建立了二元非线性回归方程，数论方法所得参数估计的标准误小于SASProc NLIN一元回归结果。结论 数论方法为多元非线性模型提供了简便易行的参数估计手段。
Number-theoretic Method for Parameters Estimation in Multivariate Nonlinear Regression with Application
, 百拇医药
Sun Xiaowu,Fang Jiqian,Department of Health Statistics,Sun Yet-Sen University of Medical Science (510089),Guangzhou
【Abstract】 Objective Developing multivariate nonlinear regression models to characterize the effect of occupational exposure in occupational epidemiology.Methods Number-theoretic(NT)method was used to estimate parametes in model.Results In the evaluation of health effects of CS2,two-outcome nonlinear model was develped,and the standard errors of estimated parameters from NT-method were smaller than those from SAS Proc NLIN.Conclusion NT method provides a simple and easy way to the estimation for multivariate nonlinear models.
, http://www.100md.com
【Key words】 Multivariate nonlinear regression Number-theoretic method CS2
引言
职业流行病学研究中常用多个指标刻划职业暴露的效应。如杨杏芬等〔1〕研究了某化纤厂工人尿中高香草酸(HVA)和香草扁桃酸(VMA)与接触二硫化碳的关系。HVA和VMA作为多巴胺代谢终产物可以提示CS2对神经化学代谢的干扰作用。为探讨这两种产物与CS2之间的暴露效应关系，需分别建立回归方程。实际上由于各指标间的相关性，我们应综合起来分析，以提供更加精确的参数估计，并确定更加符合实际的模型。对多元非线性回归模型，Bates和Watts的专著〔2〕中给出参数估计和假设检验方法，但现有统计软件未能提供相应的处理，且按他们的方法编程也复杂。本文在第二节介绍了非线性回归方法，然后应用方开泰和王元〔3〕提出的数论方法解决有关的统计推断问题；第三节通过实例分析演示方法的应用；最后讨论了方法中的有关问题。
, http://www.100md.com
模型和数论方法
1.模型与参数统计推断
设样本含量为N，每个人有M个响应变量，共依赖于p个参数β，建立多元非线性回归方程
Yn=f(xn,β)+en, n=1,…，N；
(1)
其中随机向量Yn=(Yn1,Yn2,…，YnM)对应于第n个人响应变量的观测值；f=(f1,f2,…,fM)，,fm(.，β)是第m个响应变量的模型函数，依赖于自变量Xn及参数β，En=(en1,en2,…，enM)为随机误差项。设E1，E2，…，EN相互独立且服从多元正态分布Np(0,Σ)，则有关于参数的似然函数：
, 百拇医药
(2)
。上式对Σ-1求偏导并令为零，得到(3)
代入(2)式得条件对数似然函数
(4)
从而β的极大似然估计可通过对|ETE|关于β求解极小值得到，此即多元响应模型的行列式准则。显然，这是一元响应最小二乘准则的推广。
H为对数似然函数关于β的二阶偏导阵，则H-1作为
的协方差矩阵的估计θ。的1-α置信域为下式所包围的β的区域(为β的极大似然估计), 百拇医药
(5)
这个区域虽较精确，但必须通过数值方法来确定。参数βp的1-α置信区间由下式近似得到：
(6)
2.参数估计的数论方法
现有的软件可作参数一般非线性最小二乘估计。对于多元响应行列式准则下的参数估计，Bates和Watts〔2〕给出推广的高斯-牛顿法，但目前常用的软件尚未实现。方法涉及对行列式求参数二阶偏导数，公式复杂，编程繁杂。我们这里采用方开泰和王元〔3〕提出的序贯优化数论方法(Sequential number-theoretic optimization,SNTO)求解。步骤如下：
, http://www.100md.com
步骤0：令t=0，确定初始搜索范围：p维矩形D0=〔a10，b10〕×〔a20，b20〕×…×〔ap0，bp0〕，其中ai0=βi0-ci0,bi0=βi0+ci0。βi0是βi的初始估计。
步骤1：用某一数论方法产生nt个点的点集Θt使其在Dt上均匀分布。
, 百拇医药
步骤2：对每个β∈β0UBt，按式(4)计算似然函数；求βt使得
(7)
步骤3：停止准则：若最大的两个L(β，
(β))值差距小于预先给定的δ，则停止搜索；否则进入下一步。步骤4：收缩区域：定义新的区域
(γ为预先指定的收缩比值)，；返回步骤1。3.协方差阵估计
, 百拇医药
H为对数似然函数关于β的二阶偏导阵，则H-1作为
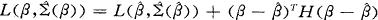
的协方差阵的估计。将似然函数在处作二阶泰勒展开，忽略高阶项则有(8)
我们在
的邻域内选择k(>p(p+1)/2)个点，计算对应的似然函数值，再拟合(8)式，即得。在勒康和罗昭容〔4〕的专著中给出类似的算法。应 用
, 百拇医药
杨杏芬等〔1〕研究了60名某化纤厂接触二硫化碳工人和48名对照组人员尿中高香草酸(HVA)和香草扁桃酸(VMA)这两种多巴胺代谢产物的变化规律。初步分析结果表明，HVA和VMA与环境CS2暴露浓度呈负相关，并符合负指数变化规律。下面的分析基于下述多元非线性回归方程：
ENVC表示环境CS2浓度。
一元非线性回归在SAS上实现，并作为多元回归估计的初始估计。按文献〔3〕提供的好格子点(good lattice point,GLP)集合表，选择生成矢量(307；1，42，229，101)，采用SNTO法经过两次循环即满足收敛要求，结果见表1。
表1 一元与多元非线性回归结果对比
, 百拇医药
一元(Proc NLIN)
多元(NT)
SE(
)SE(
)HVA
a1
2.1565
0.0686
, 百拇医药
2.1641
0.0678
b1
-0.0063*
0.0017
-0.0063*
0.0016
VMA
a2
1.1641
0.0429
1.4057
, 百拇医药
0.0426
b2
-0.0024
0.0015
-0.0029*
0.0014
*P<0.05 多元回归的参数标准误都较一元回归相应的要小。结果提示接触者导致HVA和VMA降低，该结果与以前文献报道的动物实验发现CS2干扰神经化学代谢的结果具有一致性。
讨 论
1.实际应用中评价某有害暴露会有多个指标，这些指标一般都是相关的，理应综合起来分析，以提供更加精确的参数估计，并确定更加符合实际的模型。但过去限于理论和计算手段只能分开来考虑各指标与暴露和其他影响因素的关系。本文尝试用数论方法来解决多元非线性回归的参数估计问题，经实例验证较单个响应变量的分析精度高。
, http://www.100md.com
2.自70年代末方开泰和王元应用数论方法提出“均匀设计”以来，数论方法在统计领域有了广泛的应用〔3〕。用数论方法解决统计中的优化问题有三个优点：第一，对目标函数只有连续性要求，对多峰或不连续的(如最小一乘法)目标函数仍然有效。第二，不必计算各阶微商，编制计算程序异常方便。本文的结果是用SAS/IML编写少量的语句完成计算的。但确定适当的搜索区域和选择合适足够的格子点数非常重要，这需要对资料和背景知识有充分的认识。第三，不依赖于初始值的选取。
3.一般而言，采用多元回归模型其参数的标准误估计要小于一元模型，但本文采用的协方差近似估计在只有O(N-1)阶精度。为此，或者对似然函数作更高阶近似，或探讨Bootstrap法的应用，或采用基于Bayes原理的Gibbs抽样方法，将有望提高多元响应时的协方差估计可靠性。另外，在某些参数的显著性不高或有多余的参数时，本文提出的估计协方差的方法会失效。变量筛选和数论方法如何结合是个值得研究的问题。
, http://www.100md.com
4.本文的实例分析是最简单的例子，我们今后将在复杂模型的评价、随机效应的处理及其他感兴趣的方面作有益的探索。
*本文受中华医学基金会(CMB)资助
参考文献
1.杨杏芬，等.接触二硫化碳工人尿中高香草酸和香草扁桃酸的变化.环境与职业医学论文集(1)，广州：中山医科大学环境与职业医学中心，1995；121
2.Bates DM and Watts DG.Nonlinear Regression Analysis and its Applications.New York:John Wiley & Sons,1988
3.方开泰，王元.数论方法在统计中的应用.北京：科学出版社，1994
4.韦博成.近代非线性回归分析.南京：东南大学出版社，1989
5.勒康，罗昭容.统计渐近论基础.北京：科学出版社，1993
6.SAS Inc.SAS/IML User's Guide,version 6,Cary:SAS Inc.,1992, http://www.100md.com