利用数学模型探讨百日咳发病季节特征
作者:王成科 廖清廉 吕勇
单位:王成科(四川省蓬溪县卫生防疫站 蓬溪629100); 廖清廉(四川省蓬溪县卫生防疫站 蓬溪629100); 吕勇(四川省蓬溪县卫生防疫站 蓬溪629100)
关键词:数学模型;百日咳;发病季节特征
数理医药学杂志000139
摘 要:对蓬溪县1953~1992年百日咳发病季节特征进行分析,求得发病高峰时点为3月下旬,高峰时区为2月上旬~5月上旬。结果显示,简单余弦曲线拟合可使发病率Yi的变异减少98.65%,用含第二谐量三角多项式拟合可使Yi的变异减少99.79%。
中图分类号:R 516.6
文章编号:1004-4337(2000)01-0067-03▲
, 百拇医药
大量研究资料表明,生物界广泛存在着多种与时间有关的生物节律,以此研究内容的时间生物学(Chronobiology)近年已形成一门新的独立学科[1~5]。在自然科学领域中,常有不少现象以方向或时间来度量,如疾病的发病时间、人口出生、死亡时间、心向量图的电轴角及脑血流图等。
疾病的发生是以时、日、季、半为观察单位,具有周而复始性,没有真正零点的圆形变量。圆形分布构成比法是在圆形分布的基础上,为了资料的保密,在此基础上采用构成比法来分析周期性资料。余弦模型分析是周期现象的简单模型,可用于分析角度、生物节律或时间呈周期圆变量[4~6]。本文应用此两种方法对蓬溪县1953~1992年百日咳发病季节性特征进行分析,效果良好,现报告如下。
1 材料与方法
本文资料来源于蓬溪县1953~1985年疫情资料汇编,1986~1992年资料来源于疫情年报表。将40年百日咳发病数按月合并,求月平均发病率,并取其对数。为了计算方便,每月按30天计,取每月15日为时点。圆形分布构成比法以各月发病率占全年12个月发病率总和的百分率(R),求平均角和拟合余弦曲线来分析有无季节变动或变动模式。
, 百拇医药
1.1 求平均角
式中,R为各月发病率占全年12个月总发病率的百分率,C1i=cosα,S1i=sinα,r表示集中趋势的测度,查《圆分布r值表》,若有显著性,则各月发病率有集中趋势,即有集中性。此时平均角对应的时间即为疾病发病的高峰时点,高峰时区为 ±S。
±S。
平均角 的求解有以下三条原则:
的求解有以下三条原则: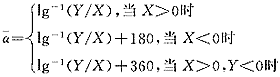
, 百拇医药
1.2 拟合余弦曲线
一条余弦曲线可用中值M、振幅A、峰值位相时 和角频率ω4个参数表示。中值为所有数据的平均值,相当于曲线的中线;振幅表示曲线振荡高于或低于中线的程度;峰值位相时表示曲线达到最高时的相角度;角频率与周期T的关系为
和角频率ω4个参数表示。中值为所有数据的平均值,相当于曲线的中线;振幅表示曲线振荡高于或低于中线的程度;峰值位相时表示曲线达到最高时的相角度;角频率与周期T的关系为 =2π/T或ω=360°/T,曲线方程以余弦函数表示:
=2π/T或ω=360°/T,曲线方程以余弦函数表示: i=M+Acos(ωti-
i=M+Acos(ωti- ) (1)
) (1)
ti是自变量,通常是有一定周期T的时间,通过三角函数变换,可将(1)式演变为: i=M+Xcosωti+Ysinωti (2)
i=M+Xcosωti+Ysinωti (2)
, http://www.100md.com
式中,X=Acos ,Y=Asin
,Y=Asin ,X、Y为参数,将(2)式的三角函数改用系数表示,则:
,X、Y为参数,将(2)式的三角函数改用系数表示,则: i=M+CiX+SiY (3)
i=M+CiX+SiY (3)
式中,Ci=cosωti,Si=sinωti,含第二谐量三角项式为: 2i=M+A1cos(ωti-
2i=M+A1cos(ωti- 1)+A2cos(2ωti-
1)+A2cos(2ωti- 2) (4)
2) (4)
, 百拇医药
将此式仿(3)式可写成: 2i=M+C1iX1+S1iY2+C2iX2+S2iY2 (5)
2i=M+C1iX1+S1iY2+C2iX2+S2iY2 (5)
式中,Xj=Ajcos j,Yj=Ajsin
j,Yj=Ajsin j,j=1,2
j,j=1,2
Cji=cos(jω)ti,Sji=sin(jω)ti
, 百拇医药
因X2+Y2=A2cos2 +A2sin2
+A2sin2 =A2
=A2
所以 (6)
(6)
(5)式中的参数,可用最小二乘法用(7)式求得其解: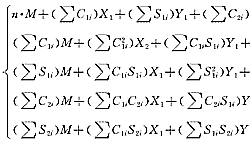
 (7)
(7)
因本例是按百日咳发病率的对数拟合的,故在求得估计月发病率 ji后,再取反对数,才是估计月发病率。
ji后,再取反对数,才是估计月发病率。
, 百拇医药
1.3 求决定系数 ,它表示用余弦曲线拟合可使发病率Yi变异减少的百分率。
,它表示用余弦曲线拟合可使发病率Yi变异减少的百分率。
2 结果
2.1 高峰时点、高峰时区
计算月平均发病率Yi及构成比R。根据表1求得:X=∑RC1i=0.2800,Y=∑RS1i=0.6520,r= =0.7090,P<0.001,表明存在集中趋势,
=0.7090,P<0.001,表明存在集中趋势, =66.7590,S=47.4590。则高峰时点为3月21日,高峰时区
=66.7590,S=47.4590。则高峰时点为3月21日,高峰时区 ±S,即为2月4日~5月9日。
±S,即为2月4日~5月9日。
, 百拇医药
表1 余弦曲线与圆形分布构成比法参数计算 月份
ti
C1i
S1i
C2i
S2i
Yi
R
RC1i
RS1i
1/10万
, 百拇医药
lg1/10万
1
0
1.000
0.000
1.000
0.000
1.9073
0.2804
0.0773
0.0773
0.0000
2
, 百拇医药
30
0.866
0.500
0.500
0.866
4.3021
0.6337
0.1743
0.1509
0.0872
3
60
0.500
, http://www.100md.com
0.866
-0.500
0.866
7.1007
0.8513
0.2877
0.1439
0.2491
4
90
0.000
1.000
-1.000
, http://www.100md.com
0.000
5.8215
0.7650
0.2359
0.0000
0.2359
5
120
-0.500
0.866
-0.500
-0.866
2.6211
, 百拇医药
0.4185
0.1062
-0.0531
0.0920
6
150
-0.866
0.500
0.500
-0.866
1.2168
0.0852
0.0493
, 百拇医药
-0.0427
0.0247
7
180
-1.000
0.000
1.000
0.000
0.3253
-0.4877
0.0132
-0.0132
0.0000
, 百拇医药
8
210
-0.866
-0.500
0.500
0.866
0.2127
-0.6722
0.0086
-0.0074
-0.0043
9
240
, 百拇医药
-0.500
-0.866
-0.500
0.866
0.1486
-0.8282
0.0060
-0.0030
-0.0052
10
270
0.000
-1.000
, 百拇医药
-1.000
0.000
0.1465
-0.8342
0.0059
0.000
-0.0059
11
300
0.500
-0.866
-0.500
-0.866
, http://www.100md.com
0.2437
-0.6131
0.0099
0.0050
-0.0086
12
330
0.866
-0.500
0.500
-0.866
0.6340
-0.1979
, http://www.100md.com
0.0257
0.0223
-0.0129
合计
-
-
-
-
-
24.6803
-0.5990
1.0000
0.2800
, 百拇医药
0.6520
2.2 发病季节变动模式
应用余弦曲线拟合求得:M=-0.5990/12=-0.0499, X1=0.3296,Y1=0.7902, X2=-0.00214, Y2=0.0422, 1=tg-1(0.7902/0.3296)=67.3585°,见表2。A1=
1=tg-1(0.7902/0.3296)=67.3585°,见表2。A1= =0.8562, A2=0.0473,
=0.8562, A2=0.0473, =116.8900。
=116.8900。
, http://www.100md.com 2.2.1 简单余弦曲线方程为: 1i=M+A1cos(ωti-
1i=M+A1cos(ωti- 1)=-0.0499+0.85602cos(ti-67.3585°)
1)=-0.0499+0.85602cos(ti-67.3585°)
由表1可见,t=60°,相当于3月15日,本例 =67.3585,相当于3月22日。根据方程拟合结果见表2。表2 余弦函数拟合计算 月份
=67.3585,相当于3月22日。根据方程拟合结果见表2。表2 余弦函数拟合计算 月份
lgYiC1i
lgYiS1i 1i
1i
, 百拇医药
Yi- 1i
1i 2i
2i
Yi- 2i
2i
lg1/10万
1/10万
lg1/10万
1/10万
1
0.2804
, 百拇医药
0.0000
0.2797
1.9041
0.0032
0.2584
1.8130
0.0943
2
0.5488
0.3169
0.6307
4.2727
0.0294
, 百拇医药
0.6566
4.5352
-0.2331
3
0.4257
0.7372
0.7992
6.2980
0.8027
0.8464
7.0210
0.0797
, http://www.100md.com 4
0.0000
0.7650
0.7403
5.4992
0.3223
0.7616
0.57756
0.0459
5
-0.2093
0.3624
0.4696
, http://www.100md.com
2.9485
-0.3274
0.4437
2.7778
-0.1567
6
-0.0738
0.0426
0.0598
1.1476
0.0692
0.0126
, http://www.100md.com 1.0294
0.1874
7
0.4877
0.0000
-0.3795
0.4173
-0.0920
-0.4008
0.3974
-0.0721
8
0.5821
, http://www.100md.com
0.3361
-0.7305
0.1860
0.0267
-0.7046
0.1974
0.0153
9
0.4140
0.7170
-0.8990
0.1262
, 百拇医药 0.0224
-0.8518
0.1407
0.0079
10
0.0000
0.8342
-0.8401
0.1445
0.0020
-0.8188
0.1518
-0.0053
, http://www.100md.com
11
-0.3066
0.5309
-0.5694
0.2695
-0.0258
-0.5953
0.2539
-0.0102
12
-0.1714
0.0990
, 百拇医药 -0.1596
0.6925
-0.0585
-0.2068
0.6212
0.0128
合计
1.9776
4.7413
-0.5988
23.9061
0.7742
, 百拇医药 -0.5988
34.7145
-0.0469
注:12M=-0.5990,6X1=∑lgYiC1i=1.9776,6Y1=∑lgYiS1i=4.7413,6X2=∑lgYiC2i=-0.1281,6Y2=∑lgYiS2i=0.2530,∑(Yi- i)2=64.7026,本表是按对数拟合的
i)2=64.7026,本表是按对数拟合的
2.2.2 含第二谐量三角多项式为: 2i=M+A1cos(ωti-
2i=M+A1cos(ωti- 1)+A2cos(2ωti-
1)+A2cos(2ωti- 2)=-0.0499+0.85602cos(ti-67.3585)+0.0473cos
2)=-0.0499+0.85602cos(ti-67.3585)+0.0473cos
, 百拇医药
(2ti-116.8900)
2.3 求决定系数R2
求得R21=0.9865,R22=0.9979,表明百日咳发病率的季节变动用简单余弦曲线拟合可使发病率Yi的变异减少98.65%,用含第二谐量三角多项式拟合可使Yi的变异减少99.79%。表明蓬溪县百日咳发病的季节变动符合余弦模式,拟合结果见表2。
3 讨论
分析疾病季节性发病高峰主要有圆形分布法、周期性回归技术、余弦函数、线状图等方法。余弦模型是用余弦函数来表示,以中值M、振幅A、峰值位相时 为主要参数来描述生物节律的变化特征,故可用于分析流行病学中昼时性、季节性、周期性资料。圆形分布构成比法与余弦模型分析法求平均角有等同的效果。因此本文应用此两种统计方法对我地1953~1992年百日咳发病的季节变动进行探讨,百日咳发病季节变动符合余弦曲线模式,求得简单余弦曲线方程为:
为主要参数来描述生物节律的变化特征,故可用于分析流行病学中昼时性、季节性、周期性资料。圆形分布构成比法与余弦模型分析法求平均角有等同的效果。因此本文应用此两种统计方法对我地1953~1992年百日咳发病的季节变动进行探讨,百日咳发病季节变动符合余弦曲线模式,求得简单余弦曲线方程为: 1i=-0.0499+0.8562cos(ti-67.3585°),含第二谐量三角多项式为:
1i=-0.0499+0.8562cos(ti-67.3585°),含第二谐量三角多项式为: 2i=-0.0499+0.8562cos(ti-67.3585°)+0.0473cos(2ti-116.7819°)。
2i=-0.0499+0.8562cos(ti-67.3585°)+0.0473cos(2ti-116.7819°)。 =67.3585,相当于3月22日。将上述两模型对实际资料进行拟合,拟合结果表明,估计百日咳月平均发病率为2.06/10万,最高月发病率为7.02/10万,最低月为0.14/10万,与实际资料基本吻合。表明用余弦模型与圆形分布构成比法分析疾病发病季节高峰特征具有等同的效果。
=67.3585,相当于3月22日。将上述两模型对实际资料进行拟合,拟合结果表明,估计百日咳月平均发病率为2.06/10万,最高月发病率为7.02/10万,最低月为0.14/10万,与实际资料基本吻合。表明用余弦模型与圆形分布构成比法分析疾病发病季节高峰特征具有等同的效果。
, http://www.100md.com
本文试用余弦模型作为蓬溪县百日咳月发病率季节变动模式,只是一种探索,并不意味着是最佳模式,也不是这种模型适用于任何地区。建立此模型必须有比较稳定的发病数为基础,因此本文采用40年百日咳发病数,力求模型的稳定。确定模型比只求平均角能提供更多的信息,但对不符合余弦曲线的资料也可用求平均角的方法来估计高峰时间,两者结合应用,互相补充。比较余弦模型的两个方程,不难看出,后式是由两条余弦曲线叠加而成的,但较简单模型复杂。
求得决定系数R21=0.9865,R22=0.9979,表明用简单余弦模型拟合可使发病率Yi的变异减少98%,用含第二谐量三角多项式拟合可使Yi的变异减少99%,但一般资料用到第二谐量即可获得满意的结果。■
参考文献:
[1] 宋开源.我国时间生物学和时间医学的近况.四川生理学杂志,1986,3:56.
, 百拇医药
[2] 赵泽贞.生理节律的应用.生物学通报,1988,2:21.
[3] 王成科,胡绍洪.应用圆形分布法分析服农药自杀高峰期.中国卫生统计,1991,3:56.
[4] 王成科.余弦模型在麻疹月平均发病率及发病季节特征研究中的应用.现代预防医学,1994,1:21.
[5] 胡克震.周期性回归.中华预防医学杂志,1988,1:22.
[6] 童建.余弦分析法在生物节律研究中的应用.中国卫生统计,1991,1:23.
收稿日期:1999-03-23, 百拇医药
单位:王成科(四川省蓬溪县卫生防疫站 蓬溪629100); 廖清廉(四川省蓬溪县卫生防疫站 蓬溪629100); 吕勇(四川省蓬溪县卫生防疫站 蓬溪629100)
关键词:数学模型;百日咳;发病季节特征
数理医药学杂志000139
摘 要:对蓬溪县1953~1992年百日咳发病季节特征进行分析,求得发病高峰时点为3月下旬,高峰时区为2月上旬~5月上旬。结果显示,简单余弦曲线拟合可使发病率Yi的变异减少98.65%,用含第二谐量三角多项式拟合可使Yi的变异减少99.79%。
中图分类号:R 516.6
文章编号:1004-4337(2000)01-0067-03▲
, 百拇医药
大量研究资料表明,生物界广泛存在着多种与时间有关的生物节律,以此研究内容的时间生物学(Chronobiology)近年已形成一门新的独立学科[1~5]。在自然科学领域中,常有不少现象以方向或时间来度量,如疾病的发病时间、人口出生、死亡时间、心向量图的电轴角及脑血流图等。
疾病的发生是以时、日、季、半为观察单位,具有周而复始性,没有真正零点的圆形变量。圆形分布构成比法是在圆形分布的基础上,为了资料的保密,在此基础上采用构成比法来分析周期性资料。余弦模型分析是周期现象的简单模型,可用于分析角度、生物节律或时间呈周期圆变量[4~6]。本文应用此两种方法对蓬溪县1953~1992年百日咳发病季节性特征进行分析,效果良好,现报告如下。
1 材料与方法
本文资料来源于蓬溪县1953~1985年疫情资料汇编,1986~1992年资料来源于疫情年报表。将40年百日咳发病数按月合并,求月平均发病率,并取其对数。为了计算方便,每月按30天计,取每月15日为时点。圆形分布构成比法以各月发病率占全年12个月发病率总和的百分率(R),求平均角和拟合余弦曲线来分析有无季节变动或变动模式。
, 百拇医药
1.1 求平均角

式中,R为各月发病率占全年12个月总发病率的百分率,C1i=cosα,S1i=sinα,r表示集中趋势的测度,查《圆分布r值表》,若有显著性,则各月发病率有集中趋势,即有集中性。此时平均角对应的时间即为疾病发病的高峰时点,高峰时区为
 ±S。
±S。
平均角
 的求解有以下三条原则:
的求解有以下三条原则: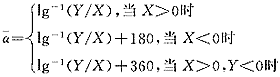
, 百拇医药
1.2 拟合余弦曲线
一条余弦曲线可用中值M、振幅A、峰值位相时
 和角频率ω4个参数表示。中值为所有数据的平均值,相当于曲线的中线;振幅表示曲线振荡高于或低于中线的程度;峰值位相时表示曲线达到最高时的相角度;角频率与周期T的关系为
和角频率ω4个参数表示。中值为所有数据的平均值,相当于曲线的中线;振幅表示曲线振荡高于或低于中线的程度;峰值位相时表示曲线达到最高时的相角度;角频率与周期T的关系为 =2π/T或ω=360°/T,曲线方程以余弦函数表示:
=2π/T或ω=360°/T,曲线方程以余弦函数表示: i=M+Acos(ωti-
i=M+Acos(ωti- ) (1)
) (1)ti是自变量,通常是有一定周期T的时间,通过三角函数变换,可将(1)式演变为:
 i=M+Xcosωti+Ysinωti (2)
i=M+Xcosωti+Ysinωti (2), http://www.100md.com
式中,X=Acos
 ,Y=Asin
,Y=Asin ,X、Y为参数,将(2)式的三角函数改用系数表示,则:
,X、Y为参数,将(2)式的三角函数改用系数表示,则: i=M+CiX+SiY (3)
i=M+CiX+SiY (3)式中,Ci=cosωti,Si=sinωti,含第二谐量三角项式为:
 2i=M+A1cos(ωti-
2i=M+A1cos(ωti- 1)+A2cos(2ωti-
1)+A2cos(2ωti- 2) (4)
2) (4), 百拇医药
将此式仿(3)式可写成:
 2i=M+C1iX1+S1iY2+C2iX2+S2iY2 (5)
2i=M+C1iX1+S1iY2+C2iX2+S2iY2 (5)式中,Xj=Ajcos
 j,Yj=Ajsin
j,Yj=Ajsin j,j=1,2
j,j=1,2Cji=cos(jω)ti,Sji=sin(jω)ti
, 百拇医药
因X2+Y2=A2cos2
 +A2sin2
+A2sin2 =A2
=A2所以
 (6)
(6)(5)式中的参数,可用最小二乘法用(7)式求得其解:
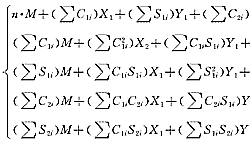
 (7)
(7)因本例是按百日咳发病率的对数拟合的,故在求得估计月发病率
 ji后,再取反对数,才是估计月发病率。
ji后,再取反对数,才是估计月发病率。, 百拇医药
1.3 求决定系数
 ,它表示用余弦曲线拟合可使发病率Yi变异减少的百分率。
,它表示用余弦曲线拟合可使发病率Yi变异减少的百分率。2 结果
2.1 高峰时点、高峰时区
计算月平均发病率Yi及构成比R。根据表1求得:X=∑RC1i=0.2800,Y=∑RS1i=0.6520,r=
 =0.7090,P<0.001,表明存在集中趋势,
=0.7090,P<0.001,表明存在集中趋势, =66.7590,S=47.4590。则高峰时点为3月21日,高峰时区
=66.7590,S=47.4590。则高峰时点为3月21日,高峰时区 ±S,即为2月4日~5月9日。
±S,即为2月4日~5月9日。, 百拇医药
表1 余弦曲线与圆形分布构成比法参数计算 月份
ti
C1i
S1i
C2i
S2i
Yi
R
RC1i
RS1i
1/10万
, 百拇医药
lg1/10万
1
0
1.000
0.000
1.000
0.000
1.9073
0.2804
0.0773
0.0773
0.0000
2
, 百拇医药
30
0.866
0.500
0.500
0.866
4.3021
0.6337
0.1743
0.1509
0.0872
3
60
0.500
, http://www.100md.com
0.866
-0.500
0.866
7.1007
0.8513
0.2877
0.1439
0.2491
4
90
0.000
1.000
-1.000
, http://www.100md.com
0.000
5.8215
0.7650
0.2359
0.0000
0.2359
5
120
-0.500
0.866
-0.500
-0.866
2.6211
, 百拇医药
0.4185
0.1062
-0.0531
0.0920
6
150
-0.866
0.500
0.500
-0.866
1.2168
0.0852
0.0493
, 百拇医药
-0.0427
0.0247
7
180
-1.000
0.000
1.000
0.000
0.3253
-0.4877
0.0132
-0.0132
0.0000
, 百拇医药
8
210
-0.866
-0.500
0.500
0.866
0.2127
-0.6722
0.0086
-0.0074
-0.0043
9
240
, 百拇医药
-0.500
-0.866
-0.500
0.866
0.1486
-0.8282
0.0060
-0.0030
-0.0052
10
270
0.000
-1.000
, 百拇医药
-1.000
0.000
0.1465
-0.8342
0.0059
0.000
-0.0059
11
300
0.500
-0.866
-0.500
-0.866
, http://www.100md.com
0.2437
-0.6131
0.0099
0.0050
-0.0086
12
330
0.866
-0.500
0.500
-0.866
0.6340
-0.1979
, http://www.100md.com
0.0257
0.0223
-0.0129
合计
-
-
-
-
-
24.6803
-0.5990
1.0000
0.2800
, 百拇医药
0.6520
2.2 发病季节变动模式
应用余弦曲线拟合求得:M=-0.5990/12=-0.0499, X1=0.3296,Y1=0.7902, X2=-0.00214, Y2=0.0422,
 1=tg-1(0.7902/0.3296)=67.3585°,见表2。A1=
1=tg-1(0.7902/0.3296)=67.3585°,见表2。A1= =0.8562, A2=0.0473,
=0.8562, A2=0.0473, =116.8900。
=116.8900。, http://www.100md.com 2.2.1 简单余弦曲线方程为:
 1i=M+A1cos(ωti-
1i=M+A1cos(ωti- 1)=-0.0499+0.85602cos(ti-67.3585°)
1)=-0.0499+0.85602cos(ti-67.3585°)由表1可见,t=60°,相当于3月15日,本例
 =67.3585,相当于3月22日。根据方程拟合结果见表2。表2 余弦函数拟合计算 月份
=67.3585,相当于3月22日。根据方程拟合结果见表2。表2 余弦函数拟合计算 月份lgYiC1i
lgYiS1i
 1i
1i, 百拇医药
Yi-
 1i
1i 2i
2iYi-
 2i
2ilg1/10万
1/10万
lg1/10万
1/10万
1
0.2804
, 百拇医药
0.0000
0.2797
1.9041
0.0032
0.2584
1.8130
0.0943
2
0.5488
0.3169
0.6307
4.2727
0.0294
, 百拇医药
0.6566
4.5352
-0.2331
3
0.4257
0.7372
0.7992
6.2980
0.8027
0.8464
7.0210
0.0797
, http://www.100md.com 4
0.0000
0.7650
0.7403
5.4992
0.3223
0.7616
0.57756
0.0459
5
-0.2093
0.3624
0.4696
, http://www.100md.com
2.9485
-0.3274
0.4437
2.7778
-0.1567
6
-0.0738
0.0426
0.0598
1.1476
0.0692
0.0126
, http://www.100md.com 1.0294
0.1874
7
0.4877
0.0000
-0.3795
0.4173
-0.0920
-0.4008
0.3974
-0.0721
8
0.5821
, http://www.100md.com
0.3361
-0.7305
0.1860
0.0267
-0.7046
0.1974
0.0153
9
0.4140
0.7170
-0.8990
0.1262
, 百拇医药 0.0224
-0.8518
0.1407
0.0079
10
0.0000
0.8342
-0.8401
0.1445
0.0020
-0.8188
0.1518
-0.0053
, http://www.100md.com
11
-0.3066
0.5309
-0.5694
0.2695
-0.0258
-0.5953
0.2539
-0.0102
12
-0.1714
0.0990
, 百拇医药 -0.1596
0.6925
-0.0585
-0.2068
0.6212
0.0128
合计
1.9776
4.7413
-0.5988
23.9061
0.7742
, 百拇医药 -0.5988
34.7145
-0.0469
注:12M=-0.5990,6X1=∑lgYiC1i=1.9776,6Y1=∑lgYiS1i=4.7413,6X2=∑lgYiC2i=-0.1281,6Y2=∑lgYiS2i=0.2530,∑(Yi-
 i)2=64.7026,本表是按对数拟合的
i)2=64.7026,本表是按对数拟合的2.2.2 含第二谐量三角多项式为:
 2i=M+A1cos(ωti-
2i=M+A1cos(ωti- 1)+A2cos(2ωti-
1)+A2cos(2ωti- 2)=-0.0499+0.85602cos(ti-67.3585)+0.0473cos
2)=-0.0499+0.85602cos(ti-67.3585)+0.0473cos, 百拇医药
(2ti-116.8900)
2.3 求决定系数R2
求得R21=0.9865,R22=0.9979,表明百日咳发病率的季节变动用简单余弦曲线拟合可使发病率Yi的变异减少98.65%,用含第二谐量三角多项式拟合可使Yi的变异减少99.79%。表明蓬溪县百日咳发病的季节变动符合余弦模式,拟合结果见表2。
3 讨论
分析疾病季节性发病高峰主要有圆形分布法、周期性回归技术、余弦函数、线状图等方法。余弦模型是用余弦函数来表示,以中值M、振幅A、峰值位相时
 为主要参数来描述生物节律的变化特征,故可用于分析流行病学中昼时性、季节性、周期性资料。圆形分布构成比法与余弦模型分析法求平均角有等同的效果。因此本文应用此两种统计方法对我地1953~1992年百日咳发病的季节变动进行探讨,百日咳发病季节变动符合余弦曲线模式,求得简单余弦曲线方程为:
为主要参数来描述生物节律的变化特征,故可用于分析流行病学中昼时性、季节性、周期性资料。圆形分布构成比法与余弦模型分析法求平均角有等同的效果。因此本文应用此两种统计方法对我地1953~1992年百日咳发病的季节变动进行探讨,百日咳发病季节变动符合余弦曲线模式,求得简单余弦曲线方程为: 1i=-0.0499+0.8562cos(ti-67.3585°),含第二谐量三角多项式为:
1i=-0.0499+0.8562cos(ti-67.3585°),含第二谐量三角多项式为: 2i=-0.0499+0.8562cos(ti-67.3585°)+0.0473cos(2ti-116.7819°)。
2i=-0.0499+0.8562cos(ti-67.3585°)+0.0473cos(2ti-116.7819°)。 =67.3585,相当于3月22日。将上述两模型对实际资料进行拟合,拟合结果表明,估计百日咳月平均发病率为2.06/10万,最高月发病率为7.02/10万,最低月为0.14/10万,与实际资料基本吻合。表明用余弦模型与圆形分布构成比法分析疾病发病季节高峰特征具有等同的效果。
=67.3585,相当于3月22日。将上述两模型对实际资料进行拟合,拟合结果表明,估计百日咳月平均发病率为2.06/10万,最高月发病率为7.02/10万,最低月为0.14/10万,与实际资料基本吻合。表明用余弦模型与圆形分布构成比法分析疾病发病季节高峰特征具有等同的效果。, http://www.100md.com
本文试用余弦模型作为蓬溪县百日咳月发病率季节变动模式,只是一种探索,并不意味着是最佳模式,也不是这种模型适用于任何地区。建立此模型必须有比较稳定的发病数为基础,因此本文采用40年百日咳发病数,力求模型的稳定。确定模型比只求平均角能提供更多的信息,但对不符合余弦曲线的资料也可用求平均角的方法来估计高峰时间,两者结合应用,互相补充。比较余弦模型的两个方程,不难看出,后式是由两条余弦曲线叠加而成的,但较简单模型复杂。
求得决定系数R21=0.9865,R22=0.9979,表明用简单余弦模型拟合可使发病率Yi的变异减少98%,用含第二谐量三角多项式拟合可使Yi的变异减少99%,但一般资料用到第二谐量即可获得满意的结果。■
参考文献:
[1] 宋开源.我国时间生物学和时间医学的近况.四川生理学杂志,1986,3:56.
, 百拇医药
[2] 赵泽贞.生理节律的应用.生物学通报,1988,2:21.
[3] 王成科,胡绍洪.应用圆形分布法分析服农药自杀高峰期.中国卫生统计,1991,3:56.
[4] 王成科.余弦模型在麻疹月平均发病率及发病季节特征研究中的应用.现代预防医学,1994,1:21.
[5] 胡克震.周期性回归.中华预防医学杂志,1988,1:22.
[6] 童建.余弦分析法在生物节律研究中的应用.中国卫生统计,1991,1:23.
收稿日期:1999-03-23, 百拇医药