重复采样试验设计的样本含量估计*
作者:任仕泉 陈峰 杨树勤
单位:四川大学管理科学与工程系(610065) 任仕泉; 南通医学院医学统计学教研室 陈峰; 华西医科大学卫生统计教研室 杨树勤
关键词:重复采样;重复测量;独立样本;样本含量估计
中国卫生统计990401 【提 要】 目的 给出重复采样试验设计的样本含量估计式。方法 探讨单组重复采样设计及配对重复采样设计的样本含量估计。结果 在相同检验效能的条件下建立了重复采样资料(非独立样本)与单一测量资料(独立样本)间样本含量的关系式。结论 以实例分析表明其结果与实际相符合。
Sample Size Estimation of Hypothesis Testing for Repeated Sampling
Ren Shiquan,et al.,Department of Management Sciences and Technology,Sichuan University(610065),Chengdu.
, 百拇医药
【Abstract】 Objective Sample size estimations of hypothesis testing for repeated sampling are given in this paper.Methods We have explored Sample size estimations of one group repeated sampling data and pairing design of repeated sampling.Results The formula of the sample sizes between repeated sampling data and independent measures data under the same power of hypothesis testing has been established.Conclusion Analysis of an example has showed that its results concide with the active situation.
, 百拇医药
【Key words】 Repeated sampling Repeated measures Independent measures data Sample size estimation
医学研究中常常因为经费不足、实验动物或试剂有限,不得不采取从同一母体(如大鼠)上重复采样(如细胞)以利用有限的资源。这类设计称为“重复采样试验设计”。由于从同一母体上采集的标本,其实验效应有一定相关(内部相关),故这类资料属非独立数据,学界常用随机效应模型〔1,2〕来分析,但对其相应的样本含量估计涉及较少。本文对单组重复采样资料及配对设计重复采样资料的相应样本含量的估计进行了探讨,并导出了在相同检验效能下重复采样资料与单一采样资料间样本含量的关系式。
重复采样的样本含量估计
对于重复采样资料,宜用随机效应模型来分析。设Yij表示对第i个个体的第j标本(i=1,…,M;j=1,…,mi)的观察值,其随机效应模型可表示为:
, 百拇医药
Yij=uj+εij
uj=μ+μj
(1)
其中μ为参数,μj~N(0, )与εij~N(0,
)与εij~N(0, 不相关,且ε1j,ε2j,…,εMj间相互独立。
不相关,且ε1j,ε2j,…,εMj间相互独立。
于是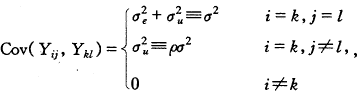
, 百拇医药 其中ρ为从同一母体所采集的标本间的相关系数。记 为样本均值,则=(1)
为样本均值,则=(1)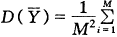
 s2)。有了样本均数的分布后,就可以对单组样本均数的检验以及配对设计样本均数的比较检验进行效能评价。如果假定检验效能为(1-β)、第Ⅰ类错误的概率为α、客观上样本均数与总体均数的差值为δ以及每个个体(或对子)的重复采样次数均为k时,那么单组重复采样设计(或配对重复采样设计)的个体数(或对子数)M即重复采样的样本含量就可以被估计出来。
s2)。有了样本均数的分布后,就可以对单组样本均数的检验以及配对设计样本均数的比较检验进行效能评价。如果假定检验效能为(1-β)、第Ⅰ类错误的概率为α、客观上样本均数与总体均数的差值为δ以及每个个体(或对子)的重复采样次数均为k时,那么单组重复采样设计(或配对重复采样设计)的个体数(或对子数)M即重复采样的样本含量就可以被估计出来。
假设给定个体(或对子)间和重复采样测量间的变异大小为σ2以及重复采样来自同一母体的标本间的相关系数为ρ,记m1=m2=…=mM=k,此时s2= 〔1+(k-1)ρ〕σ2。
〔1+(k-1)ρ〕σ2。
, 百拇医药
1.单组重复采样均数的比较检验
已知总体的均数为μ0,δ为客观上均数与μ0的差值,欲比较样本均数与总体均数,需作:
(1)单侧检验
H0∶μ=μ0,H1∶μ=μ0+δ
(2)
其中δ>0或δ<0。
在模型(1)的假设条件下,不难得到: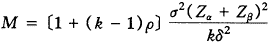
(3)
, 百拇医药
其中Zα、Zβ分别为标准正态分布的单侧上α、β分位点。由于个体(或对子)与个体(或对子)之间相互独立,如每个个体(或对子)的重复采样测量次数均为1,此时计算出来的M即为单一测量样本(独立样本)的含量估计,为了便于区分,将其记为N,则:
(4)
于是在相同的检验效能(1-β)、第Ⅰ类错误的概率α、客观上样本均数与总体均数的差值δ以及个体间(含重复采样间)变异大小σ2的条件下,由式(3)和(4),可得到单组重复采样设计样本含量与单一测量(独立样本)设计样本含量的关系式为:
(5)
, 百拇医药
(2)双侧检验 对于假设检验(2)中令δ≠0。
直接以Zα/2替代(3)、(4)式中的Zα即可分别得到: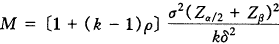
(6)
(7)
2.配对设计重复采样均数的比较检验
设有一配对样本,第i对的第j次重复采样为(Y(1)ij,Y(2)ij)(i=1,2,…,M;j=1,2,…,mi) ,对应差值Yij=
,对应差值Yij= -
- 且满足模型(1),现欲知配对重复采样资料的差值是否来自均数为零的正态总体,需检验
且满足模型(1),现欲知配对重复采样资料的差值是否来自均数为零的正态总体,需检验
, 百拇医药
H0∶μ=0, H1∶μ=δ
(8)
其中δ为客观上均数与零的差值。
其分析原理同上。
实例分析
为了研究浓度为10-8mol/L的去甲肾上腺素(NA)对大鼠脾脏T淋巴细胞增殖的影响,南通医学院生理学教研室对四只大鼠进行了实验〔3〕。每个大鼠按常规方法制备4份单个脾细胞悬液。先加入刀豆素A(Con A)和再加入10-8mol/L的NA于单个脾细胞悬液中,分别测得光密度(OD)值如表1。
表1 两种条件下对四只大鼠脾脏T淋巴细胞分别重复采样四次的OD值 鼠 号
, http://www.100md.com
先加入Con A
再加入NA
第一次
第二次
第三次
第四次
第一次
第二次
第三次
第四次
A
0.21
0.23
, 百拇医药
0.21
0.17
0.15
0.16
0.14
0.15
B
0.23
0.25
0.21
0.23
0.18
0.19
, 百拇医药
0.20
0.19
C
0.17
0.18
0.18
0.19
0.17
0.14
0.14
0.11
D
0.21
, 百拇医药
0.23
0.22
0.22
0.12
0.15
0.14
0.15
1.只加入Con A的重复采样样本OD值与总体OD值均数比较检验的样本含量估计
如果无预实验或先前经验可供参考来给定σ2的大小,即σ2为未知时,采用本实验的资料估计〔4〕得到: 2=0.00054844,内部相关系数ρ=0.52895;且M=4(鼠),k=4(次);并选取第Ⅰ类错误的概率α=0.05。利用该重复采样资料进行双侧假设检验(当指定式(2)中的|δ|<0.0325时)和单侧假设检验(当|δ|<0.0225时)的效能较低,未能达到所规定的标准80%以上。此时如果要使这些假设检验达到所规定的效能标准,必须重新进行试验设计。为了充分地利用已有的资料信息,可在此基础之上再进行大鼠的实验,这就需要估计样本含量。为此,由该资料已获得的信息有:σ2=0.00054844,重复采样间的相关系数ρ=0.52895,k=4。并假定选取第Ⅰ类错误的概率α=0.05,检验效能(1-β)=0.8。先进行双侧假设检验即式(2)中δ是否为零,按式(6)根据δ的不同取值来分别计算其重复采样四次的大鼠数M,即重复采样的样本含量估计和按式(7)来计算与其等效能的单一采样的大鼠数N即独立样本容量估计,见表2双侧一行;再进行单侧检验即式(2)中δ为一给定大小的常数,按式(3)根据δ的不同取值来分别计算其重复采样四次的样本含量估计M和与其等效能的独立样本容量估计N,见表2单侧一行。表2 单、双侧假设检验式(2)中根据δ的不同分别得到重复采样样本和独立样本的含量估计
2=0.00054844,内部相关系数ρ=0.52895;且M=4(鼠),k=4(次);并选取第Ⅰ类错误的概率α=0.05。利用该重复采样资料进行双侧假设检验(当指定式(2)中的|δ|<0.0325时)和单侧假设检验(当|δ|<0.0225时)的效能较低,未能达到所规定的标准80%以上。此时如果要使这些假设检验达到所规定的效能标准,必须重新进行试验设计。为了充分地利用已有的资料信息,可在此基础之上再进行大鼠的实验,这就需要估计样本含量。为此,由该资料已获得的信息有:σ2=0.00054844,重复采样间的相关系数ρ=0.52895,k=4。并假定选取第Ⅰ类错误的概率α=0.05,检验效能(1-β)=0.8。先进行双侧假设检验即式(2)中δ是否为零,按式(6)根据δ的不同取值来分别计算其重复采样四次的大鼠数M,即重复采样的样本含量估计和按式(7)来计算与其等效能的单一采样的大鼠数N即独立样本容量估计,见表2双侧一行;再进行单侧检验即式(2)中δ为一给定大小的常数,按式(3)根据δ的不同取值来分别计算其重复采样四次的样本含量估计M和与其等效能的独立样本容量估计N,见表2单侧一行。表2 单、双侧假设检验式(2)中根据δ的不同分别得到重复采样样本和独立样本的含量估计
, 百拇医药
(检验效能达到80%以上) δ
-0.0350
或0.0350
-0.0325
或0.0325
-0.0300
或0.0300
-0.0275
或0.0275
-0.0250
或0.0250
-0.0225
, 百拇医药
或0.0225
-0.0200
或0.0200
双侧:M
4
4
5
5
6
8
10
双侧:N
5
, http://www.100md.com
6
7
8
10
12
15
单侧:M
2
3
3
3
4
5
6
, http://www.100md.com
单侧:N
3
4
4
5
6
7
9
2.先加Con A与再加NA的配对重复采样OD值间均数比较检验的样本含量估计
由于先加Con A与再加NA组成配对并测得两OD值,按个体和重复采样的先后次序分别计算出第i个体的第j次重复采样配对OD值之差Yij,将其用来估计σ2的大小和内部相关系数ρ。于是σ2=0.00067344,ρ=0.2,k=4(次),并取第Ⅰ类错误概率α=0.05,检验效能(1-β)=0.8。对假设检验(8)的分析类似于假设检验(2),计算结果见表3。表3 单、双侧假设检验式(8)中根据δ的不同分别得到重复采样样本和独立样本的含量估计
, http://www.100md.com
(检验效能达到80%以上) δ
-0.0325
或0.0325
-0.0300
或0.0300
-0.0275
或0.0275
-0.0250
或0.0250
-0.0225
或0.0225
-0.0200
, 百拇医药
或0.0200
-0.0175
或0.0175
双侧:M
3
4
4
5
6
8
10
双侧:N
7
, http://www.100md.com
8
10
12
14
18
24
单侧:M
2
2
3
3
4
5
6
, 百拇医药
单侧:N
4
5
6
7
9
11
14
从上面的分析可以发现:如果要使较小的δ能被识别出来即其检验效能达到所规定的标准以上,必须增大重复采样的样本或独立样本的容量;由于重复采样间蕴含了一些信息,故重复采样的样本容量M通常小于独立样本含量N,且两者之间有一定的关系式,满足公式(5),这与实际相符合。讨 论
1.本文探讨了单组重复采样设计和配对重复采样设计的样本含量估计方法,其分析原理同样适用于成组设计重复采样资料、重复测量资料和纵向数据资料〔5〕,不过其公式有所变化。
, 百拇医药
2.在进行重复采样的样本含量估计时,应多注意充分利用以前的一些先验信息来指定个体间和重复采样间的变异大小σ2,内部相关系数ρ的大小以及客观均数与总体均数的差值δ的大小等,因为这些值的大小将会直接影响样本含量估计。如果没有先验信息可供利用,则最好采用预实验的办法来获得。对于第Ⅰ、Ⅱ类错误的概率大小应根据相应的错误判断所造成的危害性来确定。
3.另有两种设计方法与重复采样很相似。其一,是对同一样品的多次重复测量(repeated measures),其目的是为了提高测量的精确度,即反映测量结果是否具有稳定性或称稳定结构,其可靠程度用结构效度(cons truct validity)〔6〕来描述。这类资料的重复测量间内部相关系数通常极高,且一般与协变量无关。其二,是对同一研究对象定期或不定期地随访观察即纵向测量,其目的是考察研究对象的发生、发展或变化规律,如儿童生长发育的随访研究,某药物在体内的代谢过程等,其内部相关系数常与随访时间间隔有关〔5〕。而重复采样是从同一母体上采集的标本,这些标本间的内部相关系数通常不高,且可能与某些协变量有关。尽管在许多文献〔1,2,7〕中,将它们均称为重复测量,且其分析处理方法大致相似,但由于设计各有侧重,故因变量的协方差结构有所不同。对于应用工作者来说,尤应注意其设计方面的区分。
, 百拇医药
(特别感谢伦敦大学杨珉女士提供有关文献资料和南通医学院邱一华、彭聿平副教授提供原始数据。)
*国家自然科学基金资助项目(39500127)
参考文献
1.Longford,N.T.Random Coefficient Models.(2nd Edition),Oxford:Clarendon Press,1993.
2.Goldstein,H.Multilevel Statistical Models.(2nd Edition),London:Edward Arnold,1995,8.
3.彭聿平,等.去甲肾上腺素对T淋巴细胞增殖的影响.中国应用生理学杂志,1995,11(1):75~78.
, http://www.100md.com
4.Goldstein H.Multilevel mixed linear model analysis using iterative generalized least squares.Biometrika 1986,73:43~56.
5.Diggle,P.J.,Liang,K.Y.and Zeger,S.L.Analysis of Longitudinal Data.Oxford:Clarendon Press,1994.
6.方积乾,徐勇勇,余松林,等.医学统计学与电脑实验.上海:上海科学技术出版社,1997,240~245.
7.Lindsey,J.K.Models for Repeated Measurements.Oxford:Clarendon Press,1993., 百拇医药
单位:四川大学管理科学与工程系(610065) 任仕泉; 南通医学院医学统计学教研室 陈峰; 华西医科大学卫生统计教研室 杨树勤
关键词:重复采样;重复测量;独立样本;样本含量估计
中国卫生统计990401 【提 要】 目的 给出重复采样试验设计的样本含量估计式。方法 探讨单组重复采样设计及配对重复采样设计的样本含量估计。结果 在相同检验效能的条件下建立了重复采样资料(非独立样本)与单一测量资料(独立样本)间样本含量的关系式。结论 以实例分析表明其结果与实际相符合。
Sample Size Estimation of Hypothesis Testing for Repeated Sampling
Ren Shiquan,et al.,Department of Management Sciences and Technology,Sichuan University(610065),Chengdu.
, 百拇医药
【Abstract】 Objective Sample size estimations of hypothesis testing for repeated sampling are given in this paper.Methods We have explored Sample size estimations of one group repeated sampling data and pairing design of repeated sampling.Results The formula of the sample sizes between repeated sampling data and independent measures data under the same power of hypothesis testing has been established.Conclusion Analysis of an example has showed that its results concide with the active situation.
, 百拇医药
【Key words】 Repeated sampling Repeated measures Independent measures data Sample size estimation
医学研究中常常因为经费不足、实验动物或试剂有限,不得不采取从同一母体(如大鼠)上重复采样(如细胞)以利用有限的资源。这类设计称为“重复采样试验设计”。由于从同一母体上采集的标本,其实验效应有一定相关(内部相关),故这类资料属非独立数据,学界常用随机效应模型〔1,2〕来分析,但对其相应的样本含量估计涉及较少。本文对单组重复采样资料及配对设计重复采样资料的相应样本含量的估计进行了探讨,并导出了在相同检验效能下重复采样资料与单一采样资料间样本含量的关系式。
重复采样的样本含量估计
对于重复采样资料,宜用随机效应模型来分析。设Yij表示对第i个个体的第j标本(i=1,…,M;j=1,…,mi)的观察值,其随机效应模型可表示为:
, 百拇医药
Yij=uj+εij
uj=μ+μj
(1)
其中μ为参数,μj~N(0,
 )与εij~N(0,
)与εij~N(0, 不相关,且ε1j,ε2j,…,εMj间相互独立。
不相关,且ε1j,ε2j,…,εMj间相互独立。于是
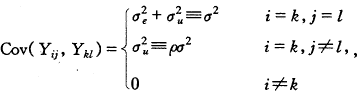
, 百拇医药 其中ρ为从同一母体所采集的标本间的相关系数。记
 为样本均值,则=(1)
为样本均值,则=(1)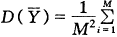
 s2)。有了样本均数的分布后,就可以对单组样本均数的检验以及配对设计样本均数的比较检验进行效能评价。如果假定检验效能为(1-β)、第Ⅰ类错误的概率为α、客观上样本均数与总体均数的差值为δ以及每个个体(或对子)的重复采样次数均为k时,那么单组重复采样设计(或配对重复采样设计)的个体数(或对子数)M即重复采样的样本含量就可以被估计出来。
s2)。有了样本均数的分布后,就可以对单组样本均数的检验以及配对设计样本均数的比较检验进行效能评价。如果假定检验效能为(1-β)、第Ⅰ类错误的概率为α、客观上样本均数与总体均数的差值为δ以及每个个体(或对子)的重复采样次数均为k时,那么单组重复采样设计(或配对重复采样设计)的个体数(或对子数)M即重复采样的样本含量就可以被估计出来。假设给定个体(或对子)间和重复采样测量间的变异大小为σ2以及重复采样来自同一母体的标本间的相关系数为ρ,记m1=m2=…=mM=k,此时s2=
 〔1+(k-1)ρ〕σ2。
〔1+(k-1)ρ〕σ2。, 百拇医药
1.单组重复采样均数的比较检验
已知总体的均数为μ0,δ为客观上均数与μ0的差值,欲比较样本均数与总体均数,需作:
(1)单侧检验
H0∶μ=μ0,H1∶μ=μ0+δ
(2)
其中δ>0或δ<0。
在模型(1)的假设条件下,不难得到:
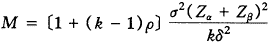
(3)
, 百拇医药
其中Zα、Zβ分别为标准正态分布的单侧上α、β分位点。由于个体(或对子)与个体(或对子)之间相互独立,如每个个体(或对子)的重复采样测量次数均为1,此时计算出来的M即为单一测量样本(独立样本)的含量估计,为了便于区分,将其记为N,则:

(4)
于是在相同的检验效能(1-β)、第Ⅰ类错误的概率α、客观上样本均数与总体均数的差值δ以及个体间(含重复采样间)变异大小σ2的条件下,由式(3)和(4),可得到单组重复采样设计样本含量与单一测量(独立样本)设计样本含量的关系式为:

(5)
, 百拇医药
(2)双侧检验 对于假设检验(2)中令δ≠0。
直接以Zα/2替代(3)、(4)式中的Zα即可分别得到:
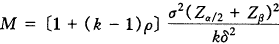
(6)

(7)
2.配对设计重复采样均数的比较检验
设有一配对样本,第i对的第j次重复采样为(Y(1)ij,Y(2)ij)(i=1,2,…,M;j=1,2,…,mi)
 ,对应差值Yij=
,对应差值Yij= -
- 且满足模型(1),现欲知配对重复采样资料的差值是否来自均数为零的正态总体,需检验
且满足模型(1),现欲知配对重复采样资料的差值是否来自均数为零的正态总体,需检验, 百拇医药
H0∶μ=0, H1∶μ=δ
(8)
其中δ为客观上均数与零的差值。
其分析原理同上。
实例分析
为了研究浓度为10-8mol/L的去甲肾上腺素(NA)对大鼠脾脏T淋巴细胞增殖的影响,南通医学院生理学教研室对四只大鼠进行了实验〔3〕。每个大鼠按常规方法制备4份单个脾细胞悬液。先加入刀豆素A(Con A)和再加入10-8mol/L的NA于单个脾细胞悬液中,分别测得光密度(OD)值如表1。
表1 两种条件下对四只大鼠脾脏T淋巴细胞分别重复采样四次的OD值 鼠 号
, http://www.100md.com
先加入Con A
再加入NA
第一次
第二次
第三次
第四次
第一次
第二次
第三次
第四次
A
0.21
0.23
, 百拇医药
0.21
0.17
0.15
0.16
0.14
0.15
B
0.23
0.25
0.21
0.23
0.18
0.19
, 百拇医药
0.20
0.19
C
0.17
0.18
0.18
0.19
0.17
0.14
0.14
0.11
D
0.21
, 百拇医药
0.23
0.22
0.22
0.12
0.15
0.14
0.15
1.只加入Con A的重复采样样本OD值与总体OD值均数比较检验的样本含量估计
如果无预实验或先前经验可供参考来给定σ2的大小,即σ2为未知时,采用本实验的资料估计〔4〕得到:
 2=0.00054844,内部相关系数ρ=0.52895;且M=4(鼠),k=4(次);并选取第Ⅰ类错误的概率α=0.05。利用该重复采样资料进行双侧假设检验(当指定式(2)中的|δ|<0.0325时)和单侧假设检验(当|δ|<0.0225时)的效能较低,未能达到所规定的标准80%以上。此时如果要使这些假设检验达到所规定的效能标准,必须重新进行试验设计。为了充分地利用已有的资料信息,可在此基础之上再进行大鼠的实验,这就需要估计样本含量。为此,由该资料已获得的信息有:σ2=0.00054844,重复采样间的相关系数ρ=0.52895,k=4。并假定选取第Ⅰ类错误的概率α=0.05,检验效能(1-β)=0.8。先进行双侧假设检验即式(2)中δ是否为零,按式(6)根据δ的不同取值来分别计算其重复采样四次的大鼠数M,即重复采样的样本含量估计和按式(7)来计算与其等效能的单一采样的大鼠数N即独立样本容量估计,见表2双侧一行;再进行单侧检验即式(2)中δ为一给定大小的常数,按式(3)根据δ的不同取值来分别计算其重复采样四次的样本含量估计M和与其等效能的独立样本容量估计N,见表2单侧一行。表2 单、双侧假设检验式(2)中根据δ的不同分别得到重复采样样本和独立样本的含量估计
2=0.00054844,内部相关系数ρ=0.52895;且M=4(鼠),k=4(次);并选取第Ⅰ类错误的概率α=0.05。利用该重复采样资料进行双侧假设检验(当指定式(2)中的|δ|<0.0325时)和单侧假设检验(当|δ|<0.0225时)的效能较低,未能达到所规定的标准80%以上。此时如果要使这些假设检验达到所规定的效能标准,必须重新进行试验设计。为了充分地利用已有的资料信息,可在此基础之上再进行大鼠的实验,这就需要估计样本含量。为此,由该资料已获得的信息有:σ2=0.00054844,重复采样间的相关系数ρ=0.52895,k=4。并假定选取第Ⅰ类错误的概率α=0.05,检验效能(1-β)=0.8。先进行双侧假设检验即式(2)中δ是否为零,按式(6)根据δ的不同取值来分别计算其重复采样四次的大鼠数M,即重复采样的样本含量估计和按式(7)来计算与其等效能的单一采样的大鼠数N即独立样本容量估计,见表2双侧一行;再进行单侧检验即式(2)中δ为一给定大小的常数,按式(3)根据δ的不同取值来分别计算其重复采样四次的样本含量估计M和与其等效能的独立样本容量估计N,见表2单侧一行。表2 单、双侧假设检验式(2)中根据δ的不同分别得到重复采样样本和独立样本的含量估计, 百拇医药
(检验效能达到80%以上) δ
-0.0350
或0.0350
-0.0325
或0.0325
-0.0300
或0.0300
-0.0275
或0.0275
-0.0250
或0.0250
-0.0225
, 百拇医药
或0.0225
-0.0200
或0.0200
双侧:M
4
4
5
5
6
8
10
双侧:N
5
, http://www.100md.com
6
7
8
10
12
15
单侧:M
2
3
3
3
4
5
6
, http://www.100md.com
单侧:N
3
4
4
5
6
7
9
2.先加Con A与再加NA的配对重复采样OD值间均数比较检验的样本含量估计
由于先加Con A与再加NA组成配对并测得两OD值,按个体和重复采样的先后次序分别计算出第i个体的第j次重复采样配对OD值之差Yij,将其用来估计σ2的大小和内部相关系数ρ。于是σ2=0.00067344,ρ=0.2,k=4(次),并取第Ⅰ类错误概率α=0.05,检验效能(1-β)=0.8。对假设检验(8)的分析类似于假设检验(2),计算结果见表3。表3 单、双侧假设检验式(8)中根据δ的不同分别得到重复采样样本和独立样本的含量估计
, http://www.100md.com
(检验效能达到80%以上) δ
-0.0325
或0.0325
-0.0300
或0.0300
-0.0275
或0.0275
-0.0250
或0.0250
-0.0225
或0.0225
-0.0200
, 百拇医药
或0.0200
-0.0175
或0.0175
双侧:M
3
4
4
5
6
8
10
双侧:N
7
, http://www.100md.com
8
10
12
14
18
24
单侧:M
2
2
3
3
4
5
6
, 百拇医药
单侧:N
4
5
6
7
9
11
14
从上面的分析可以发现:如果要使较小的δ能被识别出来即其检验效能达到所规定的标准以上,必须增大重复采样的样本或独立样本的容量;由于重复采样间蕴含了一些信息,故重复采样的样本容量M通常小于独立样本含量N,且两者之间有一定的关系式,满足公式(5),这与实际相符合。讨 论
1.本文探讨了单组重复采样设计和配对重复采样设计的样本含量估计方法,其分析原理同样适用于成组设计重复采样资料、重复测量资料和纵向数据资料〔5〕,不过其公式有所变化。
, 百拇医药
2.在进行重复采样的样本含量估计时,应多注意充分利用以前的一些先验信息来指定个体间和重复采样间的变异大小σ2,内部相关系数ρ的大小以及客观均数与总体均数的差值δ的大小等,因为这些值的大小将会直接影响样本含量估计。如果没有先验信息可供利用,则最好采用预实验的办法来获得。对于第Ⅰ、Ⅱ类错误的概率大小应根据相应的错误判断所造成的危害性来确定。
3.另有两种设计方法与重复采样很相似。其一,是对同一样品的多次重复测量(repeated measures),其目的是为了提高测量的精确度,即反映测量结果是否具有稳定性或称稳定结构,其可靠程度用结构效度(cons truct validity)〔6〕来描述。这类资料的重复测量间内部相关系数通常极高,且一般与协变量无关。其二,是对同一研究对象定期或不定期地随访观察即纵向测量,其目的是考察研究对象的发生、发展或变化规律,如儿童生长发育的随访研究,某药物在体内的代谢过程等,其内部相关系数常与随访时间间隔有关〔5〕。而重复采样是从同一母体上采集的标本,这些标本间的内部相关系数通常不高,且可能与某些协变量有关。尽管在许多文献〔1,2,7〕中,将它们均称为重复测量,且其分析处理方法大致相似,但由于设计各有侧重,故因变量的协方差结构有所不同。对于应用工作者来说,尤应注意其设计方面的区分。
, 百拇医药
(特别感谢伦敦大学杨珉女士提供有关文献资料和南通医学院邱一华、彭聿平副教授提供原始数据。)
*国家自然科学基金资助项目(39500127)
参考文献
1.Longford,N.T.Random Coefficient Models.(2nd Edition),Oxford:Clarendon Press,1993.
2.Goldstein,H.Multilevel Statistical Models.(2nd Edition),London:Edward Arnold,1995,8.
3.彭聿平,等.去甲肾上腺素对T淋巴细胞增殖的影响.中国应用生理学杂志,1995,11(1):75~78.
, http://www.100md.com
4.Goldstein H.Multilevel mixed linear model analysis using iterative generalized least squares.Biometrika 1986,73:43~56.
5.Diggle,P.J.,Liang,K.Y.and Zeger,S.L.Analysis of Longitudinal Data.Oxford:Clarendon Press,1994.
6.方积乾,徐勇勇,余松林,等.医学统计学与电脑实验.上海:上海科学技术出版社,1997,240~245.
7.Lindsey,J.K.Models for Repeated Measurements.Oxford:Clarendon Press,1993., 百拇医药