不同方法计算传染病平均发展速度的比较
作者:余善根 杜开文 吴宗秀
单位:渠县结核病防治所(635200) 余善根; 渠县卫生防疫站 杜开文 吴宗秀
关键词:
中国卫生统计990417 平均发展速度是反映某一现象在某几个单位时期中的平均发展水平。其结果减去1或100%,如得负值即为平均递减或递降,反之为递增。该指标应用十分广泛,在传染病防治中,如考核评价防治效果,分析流行规律、预测流行趋势等均常用。其计算方法有:水平法,一次平均法、二次平均法、累计法等。在实际应用中,常因计算方法不同而致结果各异,有时甚至误差较大。为此,现以不同方法对渠县1991~1995年消化道传染病(肝炎、痢疾、伤寒副伤寒)计算比较如下。
方法及公式
1.水平法:
, 百拇医药
(1)
2.一次平均法: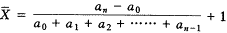
(2)
此式中若不加1则为平均递减速度。
3.二次平均法:
(3)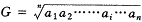
(4)
4.累计法(用切线法迭代公式计算):所谓迭代,就是先选定初始值X0,将其代入公式,如此不断重复进行,直至前后相邻的两项计算结果基本相近为止。
, 百拇医药
(5)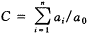
(6)
以上各式中:n为水平个数,a0为基期水平数,an为末期水平数,G为几何均数,a1、a2…ai…an-1为各期水平数,c为高次方程常数值。
结 果
渠县1991~1995年消化道传染病发病率见表1。
表1 渠县1991~1995年消化道传染病年发病率(1/10万) 年份
1991
, http://www.100md.com
1992
1993
1994
1995
发病率
295.448
94.458
78.830
88.240
72.869
1.水平法: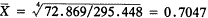
0.7047-1=-0.29523,即年均递降29.53%。
, http://www.100md.com
2.一次平均法: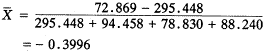
即年均递降39.96%,加上1得年平均发展速度为0.6004。
3.二次平均法
0.6023-1=-0.3977,即年均递降39.77%。
4.累计法: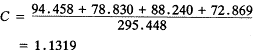
进行迭代,求正根近似值
n=4,当k=1时,Xk-1=X0,令X0=1(100%)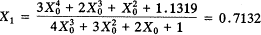
, 百拇医药
将X1代入公式得X2=0.5815,依此类推,X3=0.5564,X4=0.5558,X5=0.5558。X4与X5基本接近,可以认为X5为所求平均发展速度。
X5=0.5558-1=-0.4442,即年平均递降为44.42%。
5.以1991年为基数,用各种方法所求发展速度计算出本方法1992~1995年理论值之和与表1中1992~1995年实际值之和334.3959比较见表2。
表2 理论值与实际值比较 方法
发展速度
递降速度
, http://www.100md.com
理论值之和
理论值与实际
值之差
差率(%)
水平法
0.7047
0.2953
530.206
+195.810
58.86
一项平均法
0.6004
0.3996
, http://www.100md.com
386.200
+51.805
15.49
二次平均法
0.6023
0.3977
388.574
+54.178
16.20
累计法
0.5558
0.4442
, http://www.100md.com 334.396
+0.000
0.00
讨 论
1.本文用水平法、一次平均法、二次平均法及累计法对渠县1991~1995年消化道传染病平均发展速度计算结果比较,以累计法最为精确,其理论值与实际值之差率仅几乎为零;一次平均法,二次平均法 分别为15.49%,16.20%;水平法差率最大,为58.86%。
2.水平法计算简单,在实际工作中应用方便,但它的计算只是以a0和an为转移,当a0和an两项或任一项受偶然因素影响时,所得结果就很不合理。其他方法均是对各期发展水平的综合平均,其结果不再是取决于a0和an,因此较为科学合理,但计算较水平法复杂,特别是累计法。
, 百拇医药
3.各种方法均适用于a0>0的情况,当a0=0时,水平法和二次平均法被约束,一次平均法仍适用。累计法可应用于a0<0,但被a0=0约束。假如各期水平按一固定比例递增或递减时,则各种方法计算结果相同。如a0=1000,a1=900,a2=810,a3=729,……。其环比均为90%(发展速度),递减速度为10%。
4.综上所述,在传染病流行病学研究中,如考核评价防治效果分析流行规律、预测流行趋势等应用平均发展速度时,应根据资料实际和各种方法的适用条件选用。在适用条件下,应首选累计法,尽管该法计算较复杂,但精确度高,科学合理,且可用高次方程近似解法中的切线迭代公式直接计算,在当今电子计算机和计算器已普及的情况下,其应用亦非难事。, http://www.100md.com
单位:渠县结核病防治所(635200) 余善根; 渠县卫生防疫站 杜开文 吴宗秀
关键词:
中国卫生统计990417 平均发展速度是反映某一现象在某几个单位时期中的平均发展水平。其结果减去1或100%,如得负值即为平均递减或递降,反之为递增。该指标应用十分广泛,在传染病防治中,如考核评价防治效果,分析流行规律、预测流行趋势等均常用。其计算方法有:水平法,一次平均法、二次平均法、累计法等。在实际应用中,常因计算方法不同而致结果各异,有时甚至误差较大。为此,现以不同方法对渠县1991~1995年消化道传染病(肝炎、痢疾、伤寒副伤寒)计算比较如下。
方法及公式
1.水平法:

, 百拇医药
(1)
2.一次平均法:
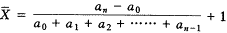
(2)
此式中若不加1则为平均递减速度。
3.二次平均法:

(3)
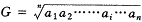
(4)
4.累计法(用切线法迭代公式计算):所谓迭代,就是先选定初始值X0,将其代入公式,如此不断重复进行,直至前后相邻的两项计算结果基本相近为止。

, 百拇医药
(5)
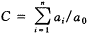
(6)
以上各式中:n为水平个数,a0为基期水平数,an为末期水平数,G为几何均数,a1、a2…ai…an-1为各期水平数,c为高次方程常数值。
结 果
渠县1991~1995年消化道传染病发病率见表1。
表1 渠县1991~1995年消化道传染病年发病率(1/10万) 年份
1991
, http://www.100md.com
1992
1993
1994
1995
发病率
295.448
94.458
78.830
88.240
72.869
1.水平法:
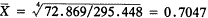
0.7047-1=-0.29523,即年均递降29.53%。
, http://www.100md.com
2.一次平均法:
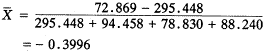
即年均递降39.96%,加上1得年平均发展速度为0.6004。
3.二次平均法

0.6023-1=-0.3977,即年均递降39.77%。
4.累计法:
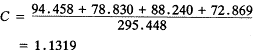
进行迭代,求正根近似值
n=4,当k=1时,Xk-1=X0,令X0=1(100%)
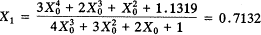
, 百拇医药
将X1代入公式得X2=0.5815,依此类推,X3=0.5564,X4=0.5558,X5=0.5558。X4与X5基本接近,可以认为X5为所求平均发展速度。
X5=0.5558-1=-0.4442,即年平均递降为44.42%。
5.以1991年为基数,用各种方法所求发展速度计算出本方法1992~1995年理论值之和与表1中1992~1995年实际值之和334.3959比较见表2。
表2 理论值与实际值比较 方法
发展速度
递降速度
, http://www.100md.com
理论值之和
理论值与实际
值之差
差率(%)
水平法
0.7047
0.2953
530.206
+195.810
58.86
一项平均法
0.6004
0.3996
, http://www.100md.com
386.200
+51.805
15.49
二次平均法
0.6023
0.3977
388.574
+54.178
16.20
累计法
0.5558
0.4442
, http://www.100md.com 334.396
+0.000
0.00
讨 论
1.本文用水平法、一次平均法、二次平均法及累计法对渠县1991~1995年消化道传染病平均发展速度计算结果比较,以累计法最为精确,其理论值与实际值之差率仅几乎为零;一次平均法,二次平均法 分别为15.49%,16.20%;水平法差率最大,为58.86%。
2.水平法计算简单,在实际工作中应用方便,但它的计算只是以a0和an为转移,当a0和an两项或任一项受偶然因素影响时,所得结果就很不合理。其他方法均是对各期发展水平的综合平均,其结果不再是取决于a0和an,因此较为科学合理,但计算较水平法复杂,特别是累计法。
, 百拇医药
3.各种方法均适用于a0>0的情况,当a0=0时,水平法和二次平均法被约束,一次平均法仍适用。累计法可应用于a0<0,但被a0=0约束。假如各期水平按一固定比例递增或递减时,则各种方法计算结果相同。如a0=1000,a1=900,a2=810,a3=729,……。其环比均为90%(发展速度),递减速度为10%。
4.综上所述,在传染病流行病学研究中,如考核评价防治效果分析流行规律、预测流行趋势等应用平均发展速度时,应根据资料实际和各种方法的适用条件选用。在适用条件下,应首选累计法,尽管该法计算较复杂,但精确度高,科学合理,且可用高次方程近似解法中的切线迭代公式直接计算,在当今电子计算机和计算器已普及的情况下,其应用亦非难事。, http://www.100md.com