测量误差非线性职业暴露效应模型参数估计的MCMC方法
作者:孙晓武 方积乾
单位:中山医科大学公共卫生学院卫生统计学教研室 广州510089
关键词:非线性回归;测量误差;随机效应;Markov chain Monte Carlo
数理医药学杂志990208
摘要 利用Markov chain Monte Carlo方法解决所涉及的一类模型的参数估计和假设检验问题,并以实例演示方法的应用。
1 问题的提出
职业流行病学研究中常用多个指标刻画暴露应用。如杨杏芬等[1]研究了某化纤厂工人尿中高香草酸(HVA)和香草扁桃酸(VMA)与接触二硫化碳浓度的关系。HVA和VMA作为多巴胺代谢终产物可以提示CS2对神经化学代谢的干扰作用。建立暴露效应关系是应采用个体的暴露浓度,但实际上我们常常只有环境平均浓度,或用个体采样仪得到少部分工人的个体浓度值,这给建立模型带来困难。若用环境浓度则带来暴露的“测量误差”,若采用个体测量值,则只能利用少量的个体观测值。Markov链蒙特卡洛(Markov chain Monte Carlo,简记为MCMC)以其处理复杂模型的灵活性和编程简单的特点,受到理论和应用研究人员的高度重视[2]。本文在分析个体浓度和环境浓度关系的基础上,用环境平均浓度结合一定的概率分布描述个体浓度规律,建立多元非线性回归方程刻画多个效应与暴露的关系,用MCMC方法估计参数,并以实际演示方法的应用。
, 百拇医药
2 模型与参数估计方法
2.1 模型
以xi表示第i个人的暴露,yi=(y1iy2i)表示结局向量。Yi与xi之间满足:
yki=akexp(-bkxi)+eki i=1,…,n;k=1,2 (1)
其中α=(a1,a2)和β=(b1,b2)为待估参数,误差项ei=(e1i,e2i)独立服从二元正态分布N(0,∑e),∑e为协方差阵。我们通常只有工人所在岗位的平均暴露浓度x*i,其个体暴露水平xi服从正态分布N(x*i,σ2x)。
, 百拇医药
2.2 MCMC方法
设α和β具有无信息先验,而∑-1e的先验为Wishart分布W(ρR,ρ),这里R为∑-1e的近似先验估计,而ρ等于∑-1e的维数时分布最平坦因而也最无信息。经过简单的代数运算得有关后验分布规律如下:
α|β,∑-1e~N(∑α Bi∑-1eYi,∑α) (2)
Bi∑-1eYi,∑α) (2) (3)
(3) (4)
(4)
, http://www.100md.com
这里
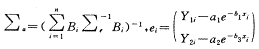
根据(2)~(4)式构造MCMC算法如下:
① α和β赋予初值;
② 按N(x*i,σ2x)产生“个体暴露”xi;
③ 依次按(2)~(4)式产生α、β和∑e的模拟抽样α(t)、β(t)和∑(t)e:α(t)直接按(2)式产生随机数得到;β(t)的更新需采用Metropolis-Hastings算法。产生∑(t)e用Odell和Feiveson[5]提出的方法;
, http://www.100md.com
④ 循环②和③N1+N2次,前N1次用于“退火”,后N2次用于计算α、β和∑e的后验分布。
以b1为例,已产生其后验分布的模拟抽样b(N1+1)1,…,b(N1+N2)1,用核估计的方法求b1的边缘密度,进而求得的最大后验估计(maximum posterior estimation,MPE)和95%可信区间。
2.3 MCMC收敛性判断
设每隔m次循环记录α、β和∑e的抽样值,在N2次中共记录n1+n2组抽样组合。将前n1次所得参数分布与后n2次所得分布作Wilcoxon检验,若MCMC已达平稳,则前述检验无差异。
, http://www.100md.com
3 应用实例
杨杏芬等[1]研究了60名某化纤厂接触二硫化碳工人和48名对照组人员尿中高香草酸(HVA)和香草扁桃酸(VMA)与接触二硫化碳浓度的关系。其中26名工人由个体采样仪采得个体浓度(SUBC)资料,其余的只有环境平均浓度。分析表明SUBC近似服从正态分布N(0.3*ENVC,0.3*ENVC),以此作为MCMC抽样模拟“个体浓度”的依据。删去缺HVA或VMA的13例,用于下面分析的有95例。
HVA/VMA与环境CS2(ENVC)浓度的模型参数估计由SAS/Proc NLIN计算获得。MCMC方法按前述算法用SAS/IML编制运算程序计算。开始5000次循环用于“退火”,再作40000次循环模拟参数的后验分布。由每隔10次循环记录的抽样值计算参数估计。
附表 SAS NLIN过程与MCMC抽样结果对比 参数
, 百拇医药
SAS/Proc NLIN
MCMC抽样
SE
95%CI
SE
95%CI
P*
a1
2.156
0.0678
, 百拇医药
2.022
2.291
2.282
0.0726
2.011
2.295
0.86
b1
0.612
0.1572
0.300
0.923
, http://www.100md.com 0.563
0.1735
0.287
0.974
0.07
a2
1.382
0.0428
1.297
1.467
1.422
0.0477
1.291
, http://www.100md.com
1.477
0.62
b2
0.236
0.1352
-0.033
0.505
0.399
0.152
-0.025
0.565
0.14
, 百拇医药 注:* 收敛性检验的P值(P>0.5提示MCMC收敛)。
上述两种方法的结果除b2的估计外基本一致,但两者原理完全不同。SAS Proc/NLIN采用最小二乘法,可信区间通过±1.96SE计算得到。整个计算过程未考虑到测量误差问题。MCMC方法考虑到测量误差的影响,所得参数估计是最大后验估计,可信区间按参数的后验分布获得。
4 讨论
本文讨论了带有测量误差的多元非线性回归模型的参数估计问题。Bates和Watts[3]的专著中给出多元非线性回归的广义Gauss-Newton法,但一般的统计软件尚未实现。而测量误差问题Diggle、Liang和Zeger[4]等将其归为随机效应的处理。目前有关非线性随机效应模型的研究很多,但都限于单反应变量。采用MCMC方法,这些都没有本质上的困难,只要选择适当的先验分布和回归函数。如测量误差模型,目前一般采用关于随机效应项一阶Taylor展开等近似方法结合EM算法进行参数估计,但近似本身带来的偏性无法估计,区间估计的可信程度难以达到预计水平。而MCMC方法中,只要引入模拟测量误差的一步,这个问题便迎刃而解。本文探讨了指数模型参数估计的MCMC方法,实际上对其他的函数形式,只须在程序中做相应的修改即可。
, http://www.100md.com
目前MCMC研究较多的Gibbs抽样,如果所有参数的后验分布的对数都是凸的(log-concave),则可采用BUGS[6]软件包实现,但指数模型不满足这个性质。另一个可能是Wakefield等[7]提出的generalized ratio of uniforms方法,相对而言,方法实现起来较为复杂。本文采用Metropolis-Hastings结合Gibbs的方法目前较频繁地用于MCMC,这个方案原理简单,编程容易,但效率相对较低,需要较多的迭代次数。
MCMC中另一个非常重要的问题为收敛性的诊断。Cowles和Carlin[8]对目前已有方法的研究表明,仅依靠少量几个综合值来判断MCMC的收敛性并不可靠,CODA[9]软件依托S-plus可以实现其中5个诊断方法。实际应用中应将理论结果和图示结合起来判断。本文应用实例的计算结果也是在多次试探性计算基础上,采用加大迭代次数的办法达到收敛。为克服参数模拟抽样间的相关性,每隔10次迭代记录一次抽样结果,最后用于参数估计的抽样值为4000个,重复计算表明结果稳定。
, 百拇医药
参考文献
1 杨杏芬等.接触二硫化碳工人尿中高香草酸和香草扁桃酸的变化.环境和职业医学论文集.广州:中山医科大学环境与职业医学中心,1995,(1):121~131.
2 Smith AFM and Robert GO(1993). Bayesian Computation via the Gibbs Sampler and Related Markov Chain Monte Carlo Methods.JRSS,B.55(1):3~23.
3 Bates DM and Watts DG(1988) Nonlinear Regression Analysis and its Applications. New York:John Wiley & Sons.
4 Diggle PJ,Liang KY and Zeger SL(1994).Analysis of Longitudinal Data. London:Chapman and Hall.
, 百拇医药
5 Odell PL and Feiveson AH(1966) A numerical procedure to generate a sample covariance matrix JASA, 61:198~203.
6 Spiegehalter D, Thomas A,Best N and Gilks W(1996) BUGS 0.5:Bayesian inference Using Gibbs Sampling, version 0.50.technical report, University of Cambridge, MRC Biostatistics Unit.
7 Wakefield JC, Smith AFM,Racine-Poon A and Gelfand AE(1994) Bayesian Analysis of Linear and Non-linear Population Models by Using the Gibbs Sampler. Applied Statistics, 4391:201~221.
, 百拇医药
8 Cowles MK and Carlin BP(1996) Markov Chain Monte Carlo Convergence Diagnopstics: A Comparative Review. JASA, 91(434):883~905.
9 Best NG,Cowles MK, and Vines K(1995) CODA:Convergence Diagnosis and Output Analysis Software for Gibbs Sampling Output, version 0.30. technical report, University of Cambridge, MRC Biostatistics Unit.
10 SAS Inc (1992) SAS/STAT,SAS/IML,Users Guide, version 6,Cary:SAS Inc.
收稿日期:1998-12-06, 百拇医药
单位:中山医科大学公共卫生学院卫生统计学教研室 广州510089
关键词:非线性回归;测量误差;随机效应;Markov chain Monte Carlo
数理医药学杂志990208
摘要 利用Markov chain Monte Carlo方法解决所涉及的一类模型的参数估计和假设检验问题,并以实例演示方法的应用。
1 问题的提出
职业流行病学研究中常用多个指标刻画暴露应用。如杨杏芬等[1]研究了某化纤厂工人尿中高香草酸(HVA)和香草扁桃酸(VMA)与接触二硫化碳浓度的关系。HVA和VMA作为多巴胺代谢终产物可以提示CS2对神经化学代谢的干扰作用。建立暴露效应关系是应采用个体的暴露浓度,但实际上我们常常只有环境平均浓度,或用个体采样仪得到少部分工人的个体浓度值,这给建立模型带来困难。若用环境浓度则带来暴露的“测量误差”,若采用个体测量值,则只能利用少量的个体观测值。Markov链蒙特卡洛(Markov chain Monte Carlo,简记为MCMC)以其处理复杂模型的灵活性和编程简单的特点,受到理论和应用研究人员的高度重视[2]。本文在分析个体浓度和环境浓度关系的基础上,用环境平均浓度结合一定的概率分布描述个体浓度规律,建立多元非线性回归方程刻画多个效应与暴露的关系,用MCMC方法估计参数,并以实际演示方法的应用。
, 百拇医药
2 模型与参数估计方法
2.1 模型
以xi表示第i个人的暴露,yi=(y1iy2i)表示结局向量。Yi与xi之间满足:
yki=akexp(-bkxi)+eki i=1,…,n;k=1,2 (1)
其中α=(a1,a2)和β=(b1,b2)为待估参数,误差项ei=(e1i,e2i)独立服从二元正态分布N(0,∑e),∑e为协方差阵。我们通常只有工人所在岗位的平均暴露浓度x*i,其个体暴露水平xi服从正态分布N(x*i,σ2x)。
, 百拇医药
2.2 MCMC方法
设α和β具有无信息先验,而∑-1e的先验为Wishart分布W(ρR,ρ),这里R为∑-1e的近似先验估计,而ρ等于∑-1e的维数时分布最平坦因而也最无信息。经过简单的代数运算得有关后验分布规律如下:
α|β,∑-1e~N(∑α
 Bi∑-1eYi,∑α) (2)
Bi∑-1eYi,∑α) (2) (3)
(3) (4)
(4), http://www.100md.com
这里

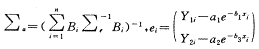
根据(2)~(4)式构造MCMC算法如下:
① α和β赋予初值;
② 按N(x*i,σ2x)产生“个体暴露”xi;
③ 依次按(2)~(4)式产生α、β和∑e的模拟抽样α(t)、β(t)和∑(t)e:α(t)直接按(2)式产生随机数得到;β(t)的更新需采用Metropolis-Hastings算法。产生∑(t)e用Odell和Feiveson[5]提出的方法;
, http://www.100md.com
④ 循环②和③N1+N2次,前N1次用于“退火”,后N2次用于计算α、β和∑e的后验分布。
以b1为例,已产生其后验分布的模拟抽样b(N1+1)1,…,b(N1+N2)1,用核估计的方法求b1的边缘密度,进而求得的最大后验估计(maximum posterior estimation,MPE)和95%可信区间。
2.3 MCMC收敛性判断
设每隔m次循环记录α、β和∑e的抽样值,在N2次中共记录n1+n2组抽样组合。将前n1次所得参数分布与后n2次所得分布作Wilcoxon检验,若MCMC已达平稳,则前述检验无差异。
, http://www.100md.com
3 应用实例
杨杏芬等[1]研究了60名某化纤厂接触二硫化碳工人和48名对照组人员尿中高香草酸(HVA)和香草扁桃酸(VMA)与接触二硫化碳浓度的关系。其中26名工人由个体采样仪采得个体浓度(SUBC)资料,其余的只有环境平均浓度。分析表明SUBC近似服从正态分布N(0.3*ENVC,0.3*ENVC),以此作为MCMC抽样模拟“个体浓度”的依据。删去缺HVA或VMA的13例,用于下面分析的有95例。
HVA/VMA与环境CS2(ENVC)浓度的模型参数估计由SAS/Proc NLIN计算获得。MCMC方法按前述算法用SAS/IML编制运算程序计算。开始5000次循环用于“退火”,再作40000次循环模拟参数的后验分布。由每隔10次循环记录的抽样值计算参数估计。
附表 SAS NLIN过程与MCMC抽样结果对比 参数
, 百拇医药
SAS/Proc NLIN
MCMC抽样

SE
95%CI

SE
95%CI
P*
a1
2.156
0.0678
, 百拇医药
2.022
2.291
2.282
0.0726
2.011
2.295
0.86
b1
0.612
0.1572
0.300
0.923
, http://www.100md.com 0.563
0.1735
0.287
0.974
0.07
a2
1.382
0.0428
1.297
1.467
1.422
0.0477
1.291
, http://www.100md.com
1.477
0.62
b2
0.236
0.1352
-0.033
0.505
0.399
0.152
-0.025
0.565
0.14
, 百拇医药 注:* 收敛性检验的P值(P>0.5提示MCMC收敛)。
上述两种方法的结果除b2的估计外基本一致,但两者原理完全不同。SAS Proc/NLIN采用最小二乘法,可信区间通过±1.96SE计算得到。整个计算过程未考虑到测量误差问题。MCMC方法考虑到测量误差的影响,所得参数估计是最大后验估计,可信区间按参数的后验分布获得。
4 讨论
本文讨论了带有测量误差的多元非线性回归模型的参数估计问题。Bates和Watts[3]的专著中给出多元非线性回归的广义Gauss-Newton法,但一般的统计软件尚未实现。而测量误差问题Diggle、Liang和Zeger[4]等将其归为随机效应的处理。目前有关非线性随机效应模型的研究很多,但都限于单反应变量。采用MCMC方法,这些都没有本质上的困难,只要选择适当的先验分布和回归函数。如测量误差模型,目前一般采用关于随机效应项一阶Taylor展开等近似方法结合EM算法进行参数估计,但近似本身带来的偏性无法估计,区间估计的可信程度难以达到预计水平。而MCMC方法中,只要引入模拟测量误差的一步,这个问题便迎刃而解。本文探讨了指数模型参数估计的MCMC方法,实际上对其他的函数形式,只须在程序中做相应的修改即可。
, http://www.100md.com
目前MCMC研究较多的Gibbs抽样,如果所有参数的后验分布的对数都是凸的(log-concave),则可采用BUGS[6]软件包实现,但指数模型不满足这个性质。另一个可能是Wakefield等[7]提出的generalized ratio of uniforms方法,相对而言,方法实现起来较为复杂。本文采用Metropolis-Hastings结合Gibbs的方法目前较频繁地用于MCMC,这个方案原理简单,编程容易,但效率相对较低,需要较多的迭代次数。
MCMC中另一个非常重要的问题为收敛性的诊断。Cowles和Carlin[8]对目前已有方法的研究表明,仅依靠少量几个综合值来判断MCMC的收敛性并不可靠,CODA[9]软件依托S-plus可以实现其中5个诊断方法。实际应用中应将理论结果和图示结合起来判断。本文应用实例的计算结果也是在多次试探性计算基础上,采用加大迭代次数的办法达到收敛。为克服参数模拟抽样间的相关性,每隔10次迭代记录一次抽样结果,最后用于参数估计的抽样值为4000个,重复计算表明结果稳定。
, 百拇医药
参考文献
1 杨杏芬等.接触二硫化碳工人尿中高香草酸和香草扁桃酸的变化.环境和职业医学论文集.广州:中山医科大学环境与职业医学中心,1995,(1):121~131.
2 Smith AFM and Robert GO(1993). Bayesian Computation via the Gibbs Sampler and Related Markov Chain Monte Carlo Methods.JRSS,B.55(1):3~23.
3 Bates DM and Watts DG(1988) Nonlinear Regression Analysis and its Applications. New York:John Wiley & Sons.
4 Diggle PJ,Liang KY and Zeger SL(1994).Analysis of Longitudinal Data. London:Chapman and Hall.
, 百拇医药
5 Odell PL and Feiveson AH(1966) A numerical procedure to generate a sample covariance matrix JASA, 61:198~203.
6 Spiegehalter D, Thomas A,Best N and Gilks W(1996) BUGS 0.5:Bayesian inference Using Gibbs Sampling, version 0.50.technical report, University of Cambridge, MRC Biostatistics Unit.
7 Wakefield JC, Smith AFM,Racine-Poon A and Gelfand AE(1994) Bayesian Analysis of Linear and Non-linear Population Models by Using the Gibbs Sampler. Applied Statistics, 4391:201~221.
, 百拇医药
8 Cowles MK and Carlin BP(1996) Markov Chain Monte Carlo Convergence Diagnopstics: A Comparative Review. JASA, 91(434):883~905.
9 Best NG,Cowles MK, and Vines K(1995) CODA:Convergence Diagnosis and Output Analysis Software for Gibbs Sampling Output, version 0.30. technical report, University of Cambridge, MRC Biostatistics Unit.
10 SAS Inc (1992) SAS/STAT,SAS/IML,Users Guide, version 6,Cary:SAS Inc.
收稿日期:1998-12-06, 百拇医药