采用Logistic模型分析钩虫感染率自然回升的变化规律
http://www.100md.com
37c医学网
作者：廖文芳 肖邦忠
单位：廖文芳(重庆市第二卫生防疫站，重庆 402160)；肖邦忠(重庆市第二卫生防疫站，重庆 402160)
关键词：
实用寄生虫病杂志000127 中图分类号：R532.12 文献标识码：B
文章编号：1005-2534(2000)01-0040-01
logistic模型多用于发育、繁殖、动态率、剂量反应率以及人口等方面的研究[1]，现将此模型试分析钩虫感染率自然回升的变化。
1 方法
1.1 logistic模型简介
, http://www.100md.com
通过建立回归方程式来分析钩虫感染率(Y变量)与防治措施停止后月数(x变量)之间的变化规律。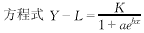
K是上下两条平行的渐近线间的距离，L是下渐近线的纵坐标，a为截距，b为斜率，x为方程自变量，e为自然对数底。
以停药后月数作自变量x，钩虫感染率为应变量Y；在X、Y图形上确定K与L，并计算出z；将X、z绘制半对数图，确定拐点；在半对数图上取相距较远的两点，即X1、z1和X2、z2，以x值代替X值，将z化成对数计算m，并化成自然对数得b，再计算a。然后将K、L、b、a代入方程式求估计感染率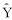
。曲线拟合度以相关指数(R2)表示。
, http://www.100md.com
式中，Y为各次检查的阳性率，Y^为各次检查的理论阳性率，n为检查次数。R2越接近于1，说明实际值与理论值越接近，曲线拟合得好。
1.2 资料
本资料为钱塘乡六村三、四村民组，于1981年2～4月经连续驱虫治疗后1月开始，每月上旬对2个村民组291人中的在家所有人员，用方口圆底盒饱和盐水漂浮法检查钩虫卵，凡第一片发现虫卵者即为阳性，若第一片为阴性，再作第二片检查，以进一步确定阴阳性。共观察13个月，观察对象年龄最小为3岁，最大为75岁，检查人数占88.0%～96.6%。
2 结果
根据各X、Y点确定K为31.6，L为0，则z=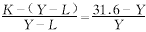
在半对数图上与z=1即(Y=
相对应的X=7.0664作为X。以拐点(70664、15.8)为原点，曲线方程的自变量x=X-X0=X-7.0664。b=0.5739(自然对数)，直线的截距Ina=0，故a=1。将上述结果代入方程。
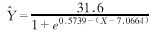
, http://www.100md.com
以此计算出各月的理论感染率(如表1)。并绘制拟合曲线。
方差分析结果(如表2)，拟合曲线后Y方面误差由Σ(Y-Y)2降至Σ(Y-Y^)2有非常显著意义(P<0.01)。
表1 钩虫病防治措施停止后感染率回升的曲线拟合 时间
(年、月)
粪检
人数
停药月数
X
阳性率(%)
Y
, 百拇医药
估计阳性率(%)
Y^
1981、5
281
1
0.7
0.9
6
281
2
2.1
1.6
7
, 百拇医药
275
3
2.2
2.8
8
272
4
6.6
4.6
9
269
5
8.2
7.4
, 百拇医药
10
269
6
8.2
11.1
11
274
7
14.6
15.4
12
280
8
, http://www.100md.com 19.6
19.3
1982、1
256
9
26.2
23.8
2
262
10
27.9
26.6
3
, 百拇医药 270
11
27.8
28.6
4
265
12
30.6
29.8
5
268
13
29.9
, http://www.100md.com 30.6
表2 钩虫感染率回升的方差分析 变异来源
df
SS
MS
F
P
总Σ(Y-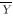
)2
12
1633.07
估计误差Σ(Y-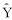)2
, http://www.100md.com
11
22.80
2.07
减少误差
1
1610.79
1610.79
777.78
<0.01
3 讨论
本资料logistic曲线拟合结果表明：钱塘乡六村钩虫病防治措施停止后一年，其感染率呈逐步回升趋势，回升速度快，幅度大，显示这类地区的钩虫感染率经防治虽可大幅度下降，然而，一但终止措施，又可迅速回升，仍须坚持防治，才能巩固成效。
, 百拇医药
本次曲线拟合度R2为0.99，方差分析具有高度显著性差异，说明理论曲线对这类地区钩虫病防治后其感染率的自然回升变化具有一定的代表性。可为今后在这类地区开展钩虫病流行病学调查和防治提供参考。
logistic曲线的上升，尤为中段为剧，这与钩虫新感染有关。当地钩虫感染季节为5～10月，6、7月为高峰，在化学治疗后的4～10月，已进入感染季节2～3个月以上，新感染的钩虫幼虫陆续移行至小肠发育为成虫并开始产卵，钩虫卵阳性人数不断增加积累，导致曲线峻陡上升。曲线两端虽上升缓慢，但仍显示这些月份也有钩虫转阳者出现，这些月份远离感染季节，可能与钩虫幼虫迁延移行和发育受阻有关[2]。
logistic模型应用广泛，使用方便，比一般曲线的描述更为合理，还可推算出理论值，值得推荐。
参考文献
1，杨树勤.中国医学百科全书医学统计学〔M〕.第1版.上海：上海科学技术出版社，1985∶168
2，钱明心，刘约翰，王小根，等.丙硫苯咪唑和噻嘧啶治疗肠道线虫病的对比观察〔J〕.中华内科杂志，1986；25(6)∶324, http://www.100md.com
单位：廖文芳(重庆市第二卫生防疫站，重庆 402160)；肖邦忠(重庆市第二卫生防疫站，重庆 402160)
关键词：
实用寄生虫病杂志000127 中图分类号：R532.12 文献标识码：B
文章编号：1005-2534(2000)01-0040-01
logistic模型多用于发育、繁殖、动态率、剂量反应率以及人口等方面的研究[1]，现将此模型试分析钩虫感染率自然回升的变化。
1 方法
1.1 logistic模型简介
, http://www.100md.com
通过建立回归方程式来分析钩虫感染率(Y变量)与防治措施停止后月数(x变量)之间的变化规律。
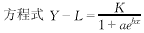
K是上下两条平行的渐近线间的距离，L是下渐近线的纵坐标，a为截距，b为斜率，x为方程自变量，e为自然对数底。
以停药后月数作自变量x，钩虫感染率为应变量Y；在X、Y图形上确定K与L，并计算出z；将X、z绘制半对数图，确定拐点；在半对数图上取相距较远的两点，即X1、z1和X2、z2，以x值代替X值，将z化成对数计算m，并化成自然对数得b，再计算a。然后将K、L、b、a代入方程式求估计感染率
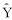。曲线拟合度以相关指数(R2)表示。, http://www.100md.com
式中，Y为各次检查的阳性率，Y^为各次检查的理论阳性率，n为检查次数。R2越接近于1，说明实际值与理论值越接近，曲线拟合得好。
1.2 资料
本资料为钱塘乡六村三、四村民组，于1981年2～4月经连续驱虫治疗后1月开始，每月上旬对2个村民组291人中的在家所有人员，用方口圆底盒饱和盐水漂浮法检查钩虫卵，凡第一片发现虫卵者即为阳性，若第一片为阴性，再作第二片检查，以进一步确定阴阳性。共观察13个月，观察对象年龄最小为3岁，最大为75岁，检查人数占88.0%～96.6%。
2 结果
根据各X、Y点确定K为31.6，L为0，则z=
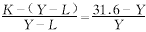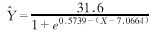
在半对数图上与z=1即(Y=相对应的X=7.0664作为X。以拐点(70664、15.8)为原点，曲线方程的自变量x=X-X0=X-7.0664。b=0.5739(自然对数)，直线的截距Ina=0，故a=1。将上述结果代入方程。, http://www.100md.com
以此计算出各月的理论感染率(如表1)。并绘制拟合曲线。
方差分析结果(如表2)，拟合曲线后Y方面误差由Σ(Y-Y)2降至Σ(Y-Y^)2有非常显著意义(P<0.01)。
表1 钩虫病防治措施停止后感染率回升的曲线拟合 时间
(年、月)
粪检
人数
停药月数
X
阳性率(%)
Y
, 百拇医药
估计阳性率(%)
Y^
1981、5
281
1
0.7
0.9
6
281
2
2.1
1.6
7
, 百拇医药
275
3
2.2
2.8
8
272
4
6.6
4.6
9
269
5
8.2
7.4
, 百拇医药
10
269
6
8.2
11.1
11
274
7
14.6
15.4
12
280
8
, http://www.100md.com 19.6
19.3
1982、1
256
9
26.2
23.8
2
262
10
27.9
26.6
3
, 百拇医药 270
11
27.8
28.6
4
265
12
30.6
29.8
5
268
13
29.9
, http://www.100md.com 30.6
表2 钩虫感染率回升的方差分析 变异来源
df
SS
MS
F
P
总Σ(Y-
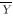)212
1633.07
估计误差Σ(Y-
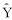)2, http://www.100md.com
11
22.80
2.07
减少误差
1
1610.79
1610.79
777.78
<0.01
3 讨论
本资料logistic曲线拟合结果表明：钱塘乡六村钩虫病防治措施停止后一年，其感染率呈逐步回升趋势，回升速度快，幅度大，显示这类地区的钩虫感染率经防治虽可大幅度下降，然而，一但终止措施，又可迅速回升，仍须坚持防治，才能巩固成效。
, 百拇医药
本次曲线拟合度R2为0.99，方差分析具有高度显著性差异，说明理论曲线对这类地区钩虫病防治后其感染率的自然回升变化具有一定的代表性。可为今后在这类地区开展钩虫病流行病学调查和防治提供参考。
logistic曲线的上升，尤为中段为剧，这与钩虫新感染有关。当地钩虫感染季节为5～10月，6、7月为高峰，在化学治疗后的4～10月，已进入感染季节2～3个月以上，新感染的钩虫幼虫陆续移行至小肠发育为成虫并开始产卵，钩虫卵阳性人数不断增加积累，导致曲线峻陡上升。曲线两端虽上升缓慢，但仍显示这些月份也有钩虫转阳者出现，这些月份远离感染季节，可能与钩虫幼虫迁延移行和发育受阻有关[2]。
logistic模型应用广泛，使用方便，比一般曲线的描述更为合理，还可推算出理论值，值得推荐。
参考文献
1，杨树勤.中国医学百科全书医学统计学〔M〕.第1版.上海：上海科学技术出版社，1985∶168
2，钱明心，刘约翰，王小根，等.丙硫苯咪唑和噻嘧啶治疗肠道线虫病的对比观察〔J〕.中华内科杂志，1986；25(6)∶324, http://www.100md.com