投资思想史珍藏版.pdf
http://www.100md.com
2020年3月12日
 |
| 第1页 |
 |
| 第5页 |
 |
| 第20页 |
 |
| 第25页 |
 |
| 第32页 |
 |
| 第95页 |
参见附件(8389KB,491页)。
投资思想史,这是一本全新的经济领域投资教程书籍,通过阅读此书读者们可以获得珍贵的投资思想,帮助你的投资更加灵活,让投资变得更加简单。

书籍介绍
当人们更多地关注财富传奇故事时,往往在浮躁的喧嚷中忽略了故事背后的思想,从而落入了只见树木不见森林的陷阱。然而,投资归根到底是思想者的活动。而这部《投资思想史》有如一股清泉,令人耳目一新。
该书从1202年斐波那契的《算经》开始写起,直至2005年的行为金融思想,时间跨度800余年,分为古代时期、古典时期和现代时期。作者马克鲁宾斯坦是美国金融学家,他以坚韧的努力对一手文献进行收集考据,为卷帙浩繁的投资学梳理出一条清晰的脉络,并以卓绝的文笔对大家思想进行功过评价。通读全书不禁让人感叹:“洛阳三月花如锦,多少功夫织得成?”
对于学者而言,该书堪称是一部参考文献手册;对于投资实务界人士而言,该书有助于投资思维的升华。面对这部波澜壮阔的投资思想史,愿您能以“闲坐小窗读《周易》,不知春去几多时”的心境品读欣赏!
作者信息
(美国)马克·鲁宾斯坦
美国金融学家,在金融界享有盛誉。他对金融衍生品和资产定价颇有研究,著有《期权市场》,对期权定价做出过重大贡献,并获奖无数。鲁宾斯坦现任加州大学伯克利分校哈斯商学院的应用投资分析专业教授,近年来由实践研究转向了总结。其他独著和合著的出版物包括《金融衍生工具》、《鲁宾斯坦论金融衍生工具》。
主目录
第一部分 古代时期:1950年之前
第二部分 古典时期:1950~1980年
第三部分 现代时期:1980年之后
克劳斯-萨吉(2001)研究了一个具有前景且十分有趣的标准多期均衡模型,它是金融学中广泛使用的模型。这两位作者允许消费者对自己的未来偏好存在不确定性,即不能完全认知自己,从而将现有的模型更一般化。虽然如此,还是假设消费者对可能的将来偏好具有概率评估。为了反映消费者缺乏自我认知,该文假设消费者偏好不仅取决于消费而且取决于不具体的状态变量。为了刻画这个均衡,他们十分聪明地假设:影响价格的未来状态能够在完全市场中被对冲掉。不过他们仍假设,那些不影响价格但影响消费者效用的未来状态是不确定的(因此市场是不完全的)。
加入的状态变量应能反映:
①能影响到效用的其他外在因素,如消费者健康或天气;
②商品的未来价格;
③不能完全市场化的资产的价值,如人力资本;
④被低估的计算结果;
⑤不完全的自我认知。
尽管这个模型具有很高的一般性,但是仍获得了一些很强且有些奇怪的结论。第一,尽管市场不完善不会影响风险的市场价格(即整体夏普率),但它会影响无风险收益,从而影响未来整体消费(整体财富)的现值,并通过这条途径影响权益风险溢价。第二,尽管时间偏好整体率是随机的,但这种不确定性不会影响风险溢价。第三,相对风险规避的波动率要比相对风险规避的水平更能影响权益风险溢价。第四,状态变量的不确定性越高,权益风险溢价就越低。有些人可能希望该文的通用性可以帮助解释风险溢价过大的问题,但不幸的是该文让权益风险溢价之谜更复杂了!
投资思想史截图
华章经典·金融投资
投资思想史(珍藏版)
A History of the Theory of Investments:My
Annotated Bibliography
(美)马克·鲁宾斯坦(Mark Rubinstein) 著
张俊生 曾亚敏 译
ISBN:978-7-111-38839-5
本书纸版由机械工业出版社于2012年出版,电子版由华章分社(北京
华章图文信息有限公司)全球范围内制作与发行。
版权所有,侵权必究
客服热线:+ 86-10-68995265
客服信箱:service@bbbvip.com
官方网址:www.bbbvip.com
新浪微博目录 译者序
前言
第一部分 古代时期:1950年之前
第二部分 古典时期:1950~1980年
第三部分 现代时期:1980年之后
注释
人名对照表纪念与追忆
金融经济学思想的荣誉译者序
英国著名的史学家柯林武德提出:一切历史都是思想史,历史学
的任务就是要重演过去的思想。当现在的出版界充斥着讲述财富故事
的书籍之时,当人们将精力更多地放在这些传奇故事之时,普罗大众
往往在浮躁的喧嚷中忽略了故事背后的思想,从而落入了只见树木不
见森林的视角陷阱。马克·鲁宾斯坦所著的这部《投资思想史》犹如
一股清泉,令人耳目一新。“现值”的思想是如何出现的?“MM”理
论背后的思想真正源自何时?卖空机制为什么是有助于稳定市场的?
投资泡沫是如何破灭的?当前流行的投资概念是如何演进的?几乎投
资学中所有核心性理论都被囊括在这部思想史中。该书可被视做一张
投资思想史全景图。
18世纪法国启蒙运动的著名思想家伏尔泰认为,对于历史人们不
应该只以堆积史实为能事,还应该达到一种哲学理论的理解境界。
《投资思想史》很好地做到了这一点。该书从1202年斐波纳契的《算
经》开始写起直至2005年的行为金融思想,时间跨度800余年,内容相
当庞杂。但是读者自该书的目录开始全然没有混乱无序之感,这在很
大程度上得益于作者深厚的学术功底与高超的写作技巧,同时更离不
开作者对分散、独立事件的解读与重构。不过,在卷帙浩繁的投资学
文献中梳理出一条清晰的脉络还是需要非凡的智慧和很大的勇气的。
《投资思想史》的作者马克·鲁宾斯坦在金融学界久负盛名。他的学
术文章多见于《金融学学刊》(Journal of Finance)和《金融经济
学学刊》(Journal of Financial Economics)等顶级刊物。能在这
些顶级刊物上发表文章的学者不在少数,但能将投资理论的发展历程
娓娓道来的学者可以说是凤毛麟角。在《投资思想史》中,他以坚韧
的努力对一手文献进行搜集考据,他以宏大的气魄将800年投资思想史
进行断代划分,他以卓绝的文笔对大家思想进行功过评价。通读全书
不禁让人感叹:“洛阳三月花如锦,多少工夫织得成?”
对于学者而言,该书堪称是一部参考文献手册。全书引用了上百
篇经典文献,每篇文献都有详尽的出处,这对学者开展相关研究甚有
帮助。鲁宾斯坦对投资学历史中出现的基础性概念与核心性思想的解
读也将有助于学术研究者把握这些内容的来龙去脉。相信该书能为投
资理论的基础性研究在中国的传播与创造有所裨益。对于投资实务界人士而言,该书有助于投资思维的升华。时至今
日,全球正面临着百年一遇的金融危机。历史经验告诉我们,危机中
往往孕育着机会。然而,机会的把握往往需要过人的智慧。《投资思
想史》虽然不会直白地告诉您如何去投资,但它会帮助您站在费雪、凯恩斯、哈耶克、阿罗、萨缪尔森和弗里德曼等大师的肩膀之上去审
视投资。
当然,对于任何一部著作我们都应抱着批判的心态去阅读。《投
资思想史》虽是大家之作,内容丰富,但它不可避免地存在着潜在的
不足。例如,该书对现代投资思想着墨偏少,尤其在行为金融方面显
得有些过于吝啬。当然,这与作者对行为金融范式的认知与一般学者
可能存在差异有关。再者,读者需要注意的是作者对某些思想的评论
只是一家之言,对于鲁宾斯坦的评论我们也应有自己的判断。
本书在中国内地的出版要感谢机械工业出版社华章公司的颜诚若
女士、王洪波女士的慧眼识珠与辛劳工作。当然,文章翻译方面的潜
在错误由译者承担。欢迎读者批评指正,我们的电子邮箱是:
junya@126.com.我们一定会虚心学习!
人类善于忘记历史,长期以来金融学这门显学也不能避免遭
此“厄运”。然而,投资归根结底是思想者的活动。那些有意在投资
学界或投资实务界大展宏图的人士应将这部《投资思想史》作为一把
开启投资思想的金钥匙。一部波澜壮阔的投资思想史即将在您的面前
展开,愿您能以“闲坐小窗读《周易》,不知春去几多时”的心境品
读欣赏!
张俊生前言
思想很少着衣而诞,而是在艰苦的累积过程中逐渐穿上华美的衣
物。在人文艺术的许多领域,为了能更深入地获取知识,有必要知道
这个领域的思想是如何演进的:这些思想是如何产生的?如何走向成
熟的?一个思想是如何催生另一个思想的?知识环境是如何滋养思想
的成长的?为什么现在看起来十分明显的思想曾让人感到十分困惑?
在社会科学中思考这些问题具有特殊的意义。在人文科学中,年
代进程是没什么意义的。例如,谁能说过去3个世纪的英国诗歌或戏剧
会超越莎士比亚的著作?在自然科学中,可以通过发现先在和永续的
自然过程而获得知识累积。然而,社会科学中的知识被发现之后可以
影响社会演进,且在相互作用中决定着后续的社会理论。
基于这种精神,我呈现在大家面前的是投资金融理论的年代发展
进程中的参考书目。不过,这不是一部投资实践史,只是偶尔会引用
到金融理论以外的现实世界。这部“投资思想史”涉猎内容广泛,包
括方法论的发展和创造理论所使用的理论工具(包含经济学、数学、心理学和科学方法)。我正在写一部将耗时多年的书卷,名曰《西方
文明史纲要》(My Outline of Western Intellectual History),这部书也将历史回溯到古代时期。
尽管这本书可作为参考书,但也可以作为一部史书从头至尾地阅
读。书中大部分内容并没有按照专题来归纳,这是因为我努力将其当
做一个完整的领域来看待,并强调一类研究是如何影响其他研究的,而以前它们可能被认为是割裂的。为了这个目的,采用编年体的形式
看起来是比较恰当的,因为后来出现的思想不能影响先前出现的思
想,而只会相反。
我们可将金融经济学的历史分为三个阶段:①1950年之前的古代
时期;②1950~1980年的古典时期;③1980年之后的现代时期。大约
在1980年之后,古典时期的理论基础面临越来越多的挑战。
在大量的金融研究中,我只能选择很小比例的文献。有些文章之
所以重要是因为它们撒播下了思想的种子,提出了正确的问题,或者
发展了重要的经济直觉;有些文章则在不同思想之间进行了十分有效
的沟通;而另外一些文章之所以重要是因为它们将早期的概念定形、理顺假设并用数学给予支持。尽管我努力在这三类研究中做到平衡,但我还是将更多笔墨放在了前两类研究上。未发表的手稿只有满足如
下两个条件之一才被编选入内:①被广泛地引用;②在其他作者公开
发表的论文出现很久之前,其包含的思想就在该手稿中出现。如果某
些文献回顾对解释思想的渊源有帮助的话,我也会将其收录在内。对
一些重要结论的数学解释或证明也在书中有所展示,它基本上是对文
字模糊表述的补充。不过,这些证明对理解来说并不是必需的。
读者也应该理解本书还有很多工作要做。许多重要的研究未被提
及,并不是因为我认为它们不重要而是因为我还没有获得这些文献。
因此,这部史书是不完整的,尤其是1980年后的内容还有很多欠缺。
尽管本书将非理性主义者的思想追溯到古代与古典时期,但是本书对
现代日益丰富的“行为金融”文献提及甚少。不过,出版商还是鼓励
我整理手头已有的文献,因为他们感觉即便这类著作还处于发展时期
但还是十分有用的。希望本书的新版本将能弥补这个缺陷。
投资理论的历史发展得益于许多著名经济学家的著作。20世纪的
经济学家,如弗兰克·奈特、欧文·费雪、约翰·梅纳德·凯恩斯、弗里德里希·哈耶克、肯尼思·阿罗、保罗·萨缪尔森、米尔顿·弗
里德曼、佛朗哥·莫迪利亚尼、杰克·赫希雷佛、詹姆斯·托宾、约
瑟夫·斯蒂格利茨、罗伯特·卢卡斯、丹尼尔·卡尼曼、阿莫斯·特
沃斯基以及乔治·阿克洛夫都留下了他们的印记。一些非经济学家在
这个世纪也对金融学贡献颇丰,包括约翰·冯·诺伊曼、伦纳德·萨
维奇、约翰·纳什、莫里斯·肯德尔。进一步向前回溯,尽管丹尼尔
·伯努利和路易斯·巴舍利耶的贡献已经广为人知,但是像斐波纳
契、布莱斯·帕斯卡、皮埃尔·费马、克里斯汀·惠更斯、亚伯拉罕
·棣莫弗、埃德蒙·哈雷这些人的著作还鲜为人知但又十分重要。
可能这个领域与其他领域一样面临着学者忽视思想渊源的问题,我对此感到沮丧。尽管一些学术文章和著作声称是历史回顾,但还是
经常过于简单地描绘成熟理论的发展轨迹,而将太多原创性思想只归
功于少数学者。无疑本书也可能存在这样的缺陷,但我希望问题没有
以前那么严重。一本著作可能淹没在逝去的历史之中,甚至有可能这
本著作要比后来出现的且广为引用的文章都要优秀。
例如,问问你自己是谁最先提出了下列思想:
现值MM定理
普拉特-阿罗风险规避指标
马科维茨的均值-方差投资组合理论
戈登增长公式
资本资产定价模型
布莱克零贝塔模型
考克斯-罗斯-鲁宾斯坦的二叉树期权定价模型
卢卡斯交易模型
米尔格罗姆-斯托克利无交易定理
从个人理性假定推出预期效用
风险中性概率下的鞅定价
动态完整
随机游走与理性市场的联系
用非平稳方差来描述证券价格的随机过程
上偏股价、异质信念与卖空约束之间的假设关系
规模效应
超常盈余增长模型
前景理论
在上述大多数例子中,思想出现的实际时间要比一般人所认为的
起源提前许多年,偶尔会提前几十年甚至几百年。在某些情况下,独
立且近乎同时的发现者却很少甚至从未被提及,这多少证明了斯蒂芬
·施蒂格勒的得名法则,即科学思想从未以其最初发现者的名字来命名。包括施蒂格勒法则自身也是这样,该法则最初的提出者实际是社
会学家与科学哲学家罗伯特K.默顿。金融经济学中的一个著名例子就
是MM定理,其实在莫迪利亚尼和米勒提出该命题的前20年,约翰·伯
尔·威廉姆斯就在1938年出版的著作中做了精彩的探讨。如果这项创
新性的洞察能在当时广为知晓且得到仔细研究,那么我们受困扰的时
间就可以减少几十年。有关默顿的另一个例子是“戈登增长公式”。
不幸的是,一旦这类错误发生就很难纠正。事实上,这个错误已经根
深蒂固,即便是最杰出的著作也未必能改变业已形成的习惯。
此外,研究者可能没有意识到某些理论的基础工作在多年前就已
经被发现。一个著名的例子是布莱克-斯科尔斯期权定价模型。尽管这
个模型是在20世纪70年代得到发展的,并且无疑是金融经济学中最为
重要的发现之一。但事实上,肯尼思·阿罗在20年前的1953年就已经
提出非常类似的观点。反过来,阿罗的想法在3个世纪之前布莱斯·帕
斯卡与皮埃尔·费马之间的通信集中隐隐地有所体现。一个科学领域
的进步通常会借鉴其他领域的方法,尤其是原本用于其他目的的数学
工具。历史研究的副产品之一就是能发现原本看似无关的工作之间的
联系。
有人会问,为什么学术领域会对自己的渊源不求甚解。历史是由
胜利者重新书写的。学生经常依赖于自己的导师来了解学科历史,而
导师又过分依赖于他自己的导师,依此类推。很少有学生会拒绝现存
的引用方式,而去图书馆书架上翻找古旧书籍和期刊来寻找他们所使
用思想的真正渊源。学者与大多数人一样,他们偏爱将成就归因于那
些相对出名的人或那些在发展这个思想方面写了几篇文章或花了数年
时间的人,而那些非主流的人士(可能是使用的方法或时机方面)即
便研究的更早更原创,还是处于不利的位置。绝好的一个例子就是
A.D.罗伊在均值-方差投资组合方面的基础性文章,就连哈里·马科维
茨也承认希望自己能与罗伊共享投资组合理论之父的荣誉。1罗伯特K.
默顿将之称为“马太效应”。这个典故来源于《马太福音》(第25章
第29节):“因为凡有的,还要加给他,叫他有余;没有的,连他所
有的,也要夺过来”。
当然,并不只有金融学才倾向于忽视自己的起源。例如,算术被
认为是艾萨克·牛顿和戈特弗里德·威廉·莱布尼兹发明的。但事实
上算术的发明可以追溯到古希腊时期。尤其是安提丰、欧多克斯、阿
基米德在使用“穷举的方法”的时候预期到了可采用极限和积分的概
念来决定几何物体的面积和体积(例如,估计圆的面积时,在圆中镶入正规多边形,随着多边形的边数无穷增加,多边形就可以近似估计
圆的面积)。尽管伽利略并没有用数学公式来正式表示,但他有关物
体运动的著作已经暗含如下内容:物体的运动速度是距离相对于时间
的一阶导数,加速度是距离相对于时间的二阶导数。皮埃尔·费马设
计出了正切法,今天我们仍在使用这种方法,它可用于判定函数的最
大值和最小值。艾萨克·巴罗使用微分的方法去寻找一个曲线的切
线。并提出了两个函数的乘积和商的微分定理、X的幂函数微分定理以
及隐函数的微分定理。
与大多数历史不同,有关金融学思想起源的大多数被遗忘的事实
都能在那里等待我们的发掘,在图书馆书架上的古旧书籍中,在过去
的期刊中(现在大多可以以电子版形式获得)我们都能发现这些思
想。很多投资理论史只是被胜利者重新书写过,最初雏形被修正过而
已。在本书中,我会竭力去探究这些思想的渊源。对于书中所引用到
的每一篇文章、每一本著作,我的目标都是明确它们对这个领域的边
际贡献。
如同莎士比亚名著《麦克白》中的三个女巫一样拥有后见之明,我能“窥视时间的种子,能说出其中哪一粒能发芽,哪一粒不能成
长”。拥有了这项优势,我在那些曾一度被认为很有前景但最终被证
明是死胡同的研究上(例如股价的稳定帕累托假设)没有花费太多精
力。
不过,我自知本书省略了许多十分重要的发现(部分原因是因为
我还没有得到这些文献)或可能将投资思想追溯到不正确的源头,可
能并没有发现更早的著作。另一方面,我也可能犯历史学家惯有的毛
病,即用后世看起来重要或正确的观点来解释书面记录,这可能是有
偏见的。我希望读者能够原谅我。我也从默顿·戴维斯那里获得了一
些帮助,为此对他表示公开的致谢。我也请求读者能提出建设性的意
见让我知晓错误,以便在以后的版本中修正。
马克·鲁宾斯坦
加州,伯克利
2006年元月第一部分 古代时期:1950年之前
1202年
斐波纳契或称比萨大公(1170—1240)出版了《算经》(Liber
Abaci)一书。该书最近由劳伦斯E.西格勒翻译成《斐波纳契的算经:
比萨大公算经的现代英译本》(Fibonacci's Liber Abaci:A
Translation into Modern English of Leonardo Pisano's Book of
Calculation)(Springer-Verlag,2002年)。1478年
未 知 名 的 作 者 出 版 了 《 翠 维 索 算 术 》 ( The Treviso
Arithmetic)一书。该书由戴维·尤金·史密斯翻译成英文,见弗兰
克J.施维茨所编著的《资本主义与算术:15世纪的新数学,包括1478
年〈翠维索算术〉全文》(Capitalism and Arithmetic:The New
Math of the 15th Century Including the Full Text of the
Treviso Arithmetic of 1478)(LaSalle,IL:Open Court,1987
年)。1761年
埃德蒙·哈雷(1656年11月8日—1742年1月14日)所著的《论复
利》(Of Compound Interest)在哈雷逝世后出版。见亨利·舍温编
著的《舍温算表》(Sherwin's Mathematical Tables)(W.and
J.Mount,T.Page and Son,1761年)。
斐波纳契数列、现值、合伙制、永续年金、资本预算
斐波纳契(1202)因为将阿拉伯数学符号引入欧洲而闻名于世。
阿拉伯数字最早可能于公元后第一个千年的中期形成于印度,其后逐
渐被阿拉伯商人和学者所学习。斐波纳契在北非的旅行中学到了阿拉
伯数字。在书中的第一章,他是这样开篇的:
如下是印度人使用的九个数字:9,8,7,6,5,4,3,2,1。用
这九个数字,再加上0这个符号,任何数字都既能被书写也能被示范。
在这本小册子出版后,用笔墨计算的阿拉伯数字取代了算盘的地
位。这本书也提出了著名的斐波纳契数列,1,1,2,3,5,8,13,…
《算经》这本书在现值计算发展中的作用却没有得到足够的重
视,直到最近才被威廉N.戈茨曼发现 [1]。斐波纳契通过几个数学例子
来说明他的计算方法。其中对投资学有四个方面的应用:①在合伙人
成员中进行公平的利润分配 [2];②序列投资的利润计算,其中包括中
间撤出投资 [3];③终值的计算 [4];④现值的计算 [5]。他对问题①的
解答很简单:将利润按照投入资本的比例来分配,这个答案在今天看
来是显而易见的。关于问题③的举例,西格勒是这样翻译的:
有个人在一家银行存入100英镑,每英镑每个月能获得4便士的利
息。他每年取出30英镑。那么他需要花多少时间才能把钱全部取出
来?(p.384)
斐波纳契的计算结果是,那个人的钱在银行的时间是6年零8天零
(12)(39)5个小时。上述表达式是斐波纳契所使用的符号,按照
今天的表示方法每一部分的分母应等于该分母与所有右边分母的乘
积,如12实际上表示的是(12×19)而小时数就是所有部分的加总和。因此,按照现代的符号表示的小时数等于5小时+(39)小时
+(118)小时= 小时。值得注意的是,尽管斐波纳契的符号
已经被废弃,但当度量小数量单位时还是很有用的。例如,斐波纳契
将会这样来表示5周零3天零4小时零12分零35秒:(3560)(1260)
(424)(37)5。
在问题④中,斐波纳契通过对两只年金现值进行排名的方式演示
了现值的使用。两只年金的区别仅在于获得报酬的周期不同,利息再
投资的利率都是每个季度2%:两只年金每年都各支付300个金币,不同
在于其中一只年金每季度支付75个金币,而另外一只年金则在每年年
末支付300个金币。
由于复利的存在,固定利率下的现值是几何序列的加权求和。戈
茨曼推测,斐波纳契的利息概念可能为他提出著名的无穷级数概念提
供灵感。不幸的是,我们对斐波纳契知之甚少,这样的猜测还不能被
证实。
在斐波纳契之后,阿拉伯数字在欧洲得到广泛的使用,尤其是用
于商业目的。一位不知名的作者所著的《翠维索算术》(1478)是迄
今已知的最早的算术书,它试图普及阿拉伯数字系统。该书在开篇描
述了如何使用阿拉伯数字来计数、加、减、乘、除——这与今天使用
的程序是一样的。在那个时期,数字刚刚演化成现代所使用的形式。
例如,用 表示零的方式在1275年后销声匿迹。其中部分原因可能
要归因于《翠维索算术》,因为印刷技术可能迫使书写标准化。不
过,加、减、乘、除等符号要到很晚才被引入。“+”和“-”出现
在1489年,“×”出现在1631年,“÷”出现在1659年。既然谈到这
个问题,我们就展开一下。“√”出现在1525年,“=”出现在1557
年,“<”和“>”出现在1631年,“∫”出现在1675年(由戈特弗
里德·威廉·莱布尼兹发明),“f(x)”出现在1735年(由列昂哈
德·欧拉发明),“dxdy”于1797年由约瑟夫-路易斯·拉格朗日提
出。用小数表示分数直至1585年才出现。用字母表示等式中的未知数
直到1580年左右才在弗兰克斯·韦达(1540—1603)的公式中出现。
约翰·纳皮尔于1614年发明了对数,并在1617年将小数符号引入欧
洲。这些数学运算是通过一些事例来演示的。合伙制可以追溯到公元
前2000年的巴比伦王国。这种商业组织形式为长期需要大笔资金的投
资提供了一种融资方式。在信奉基督教的欧洲,禁止放高利贷收取利
息,合伙制则提供了一种迂回的方式。《翠维索算术》这本书中
(p.138)提出的第一个合伙制问题是这样的:
有三个商人共同搭伙投资。第一个人名叫皮耶罗,第二个人名叫
保罗,第三个人名叫朱安妮。皮耶罗投入112个杜卡托,保罗投入200
个杜卡托,朱安妮投入142个杜卡托。过了一段时间,他们发现已经赚
了563个杜卡托。问每个人应分多少个杜卡托才是公平的。
建议的答案是:根据他们各自的投资额按照比例来分配利润。这
个原则与斐波纳契在《论公司》提出的原则一样。第二个合伙制问题
更有趣(p.138):
有两个商人,分别叫做桑巴斯提亚诺和贾科莫,他们合伙投资来
赚钱。桑巴斯提亚诺在1472年1月1日投入了350个杜卡托,贾科莫在
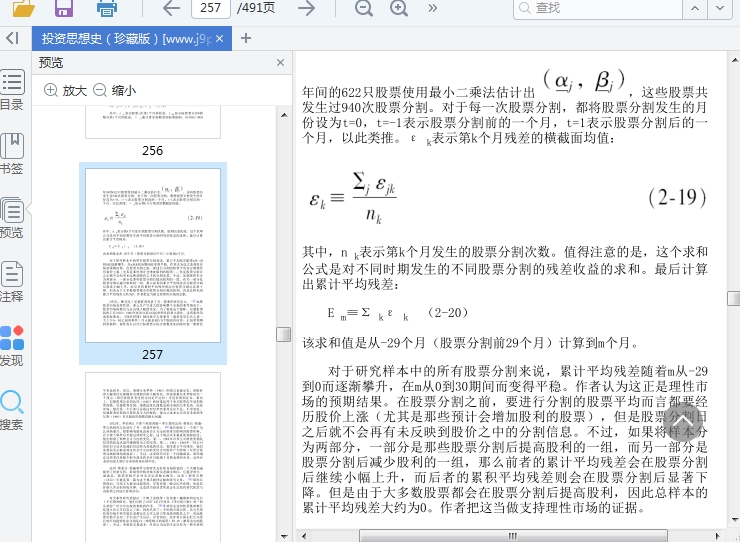
1472年7月1日投入了500个杜卡托和14个格罗西。到了1474年1月1日,他们发现已经赚到了622个杜卡托。问每个人分多少?
首先将每个人的投资转换为同一计量单位,即桑巴斯提亚诺投入
8400个格罗西,贾科莫投入12014个格罗西。《翠维索算术》这本书通
过两人各自的投资月数来调整投资时点的差异:
桑巴斯提亚诺:8400×24=201600贾科莫:12014×18=216252
而 后 根 据 各 自 所 占 的 比 例 来 分 配 。 两 数 之 和 是
201600+216252=417852 。 因 此 , 桑 巴 斯 提 亚 诺 获 得
622× ( 201600417852 ) =300 杜 卡 托 , 贾 科 莫 获 得
622×(216252417852)=322个杜卡托。
现代的分析师要解决这个分配问题需要区分两种情况:贾科莫的
滞后投资是事先约定好的呢,还是在临近投资时才决定的。在第一种
情况下,他应当知道利率才能计算出公平的分配利润;在第二种情况
下,他应当知道1472年7月1日那天合伙体中每股的价值。尽管《翠维
索算术》的作者提出了一个有趣的问题,并且可能从斐波纳契那儿学
了不少东西,但是他的答案表明他并没有理解斐波纳契复杂的现值分
析。到了16世纪,尽管高利贷在法律上受到限制,但斐波纳契有关现
值的著作仍得到了更好的认知。例如,吉恩·川辰特于1637年 [6]提出
了这么一个问题:一只永续年金每季度支付4%的利息,而另外一只定
期年金每季度支付5%的利息共计41个季度,问哪只年金的现值最高?
川辰特是这样解决这个问题的:首先计算每季度1%的年金在第41个季
度的终值,接着计算从第41季度开始每季度支付5% [7]的永续年金在第
41季度的现值,将两个数字比较后就能知道哪只年金的现值最高。在
川辰特的书中还包含了第一张现值折现因子表。
在没有计算机的远古年代,要判断利率对合约的影响,那么一定
要在快速计算方法上花大工夫。这包括使用对数、算表以及现值问题
的现成答案。埃德蒙·哈雷通过望远镜观察对南半球的星体进行了编
撰归类,发明了第一张气象分析表,出版了早期的人口死亡率表,当
然最著名的是他首先计算出彗星的轨道。他在金融经济学方面的贡献
也颇为称道。哈雷(1761)推演出年金现值公式(可能并不是最先推
演出的):[X(r-1)][1-(1r T)],这个年金开始于第一年年
末,持续期是T年。r表示1加上年利率,X表示从年金中每年获得的现
金额。对这个公式相对较早的另一个推演版本可以在费雪的作品中找
到(1906)。
尽管用现值来估值出现的比较早,但最先提出任何资本项目都应
当使用现值来评估的思想可能要归属费雪(1907)。使用套利的思
想,他对项目现金流与证券投资组合现金流进行了比较,其中证券投
资组合现金流是与项目相匹配的。不过,根据福尔哈伯和鲍莫尔
(1988)的说法,无论是《哈佛商业评论》从1922年创刊到第二次世
界大战,还是1948年前使用的公司财务方面的教材都没有在资本预算
中提到过现值。直到约尔·迪安(1951)的著作出版 [8]之后,现值的
使用才广为流行。最近,根据约翰R.格雷厄姆和坎贝尔·哈维
(2001)的研究 [9],大多数大型企业在资本预算决策中都使用一些形
式的现值计算。1494年
卢卡·帕乔利(约1445—1517)出版了《算术、几何与比例学总
论 》 ( Summa de arithmetica , geometria , proportioni et
proportionalita)(Everything about Arithmetic,Geometry and
Proportions)一书。其中,有关会计学的内容见《详论会计与记录》
(Particularis de computis et scripturus)。由A.冯·贾巴斯塔
托翻译成英文,见《卢卡·帕乔利对复式记账的探索:威尼斯1494》
( Luca Pacioli's Exposition of Double-Entry Bookkeeping :
Venice 1494)。
点数问题、会计、借与贷、会计恒等式、资产、负债和权益、净
盈余关系、账面价值与市场价值、配比原则、一致性原则
帕乔利(1494)承认他借鉴了欧几里得(约公元300年 [10])和斐
波纳契(1202)的思想归纳了算术、代数、几何和三角学的基本原
则。对我们来说更为重要的是,帕乔利提出了“点数问题”,他因此
而广受赞誉。“点数问题”最终促成了现代概率论在17世纪的爆炸式
发展(当然也有证据表明这个问题的起源可能会更早些):
选手A和选手B正在打球赛。他们同意直到一方赢得6局时就停止。
但比赛在A赢得5局B赢得3局的时候停止了。问如何分配赌注?
帕乔利的答案很简单(但不正确):根据每个人所赢的局数来按
比例分配。因此,如果赌注是56个金币,那么选手A应获得35个金币,选手B获得21个金币。
不过,帕乔利的书因其对会计的影响而闻名。古时候的会计只是
简单地列示出存货的物理量。后来会计方法把这些项目按照单一货币
的形式统一成共同的度量单位。这就变成列示“入账”和“出账”,本质上是一张说明现金来源和使用的现金表。这样一来,封建领主就
可以监督分发财物的管家。现代形式的复式记账的起源可不是很清
晰。我们知道在意大利的西耶耶(Siena)有一家名叫加勒尼
(Gallerani)公司的商业企业早在1305年就使用了复式记账的方法 [11]。尽管帕乔利并没有发明复式记账法,但是由于他在这部影响深远
的著作中深入地阐述了复式记账法,因此他通常被视为这种方法的创
始人,并被尊称为“会计学之父”。在他这本书中有关会计学内容的部分,即“详论会计与记录”这部分内容,帕乔利写道:“这种威尼
斯人所使用的方法是诸多方法中最受推崇的,并可将其当做其他方法
的指南”(p.42)。他甚至训诫会计师,如果他们的账目借贷不相
等,那么晚上都睡不安生。对财务会计习俗史的进一步讨论已经超出
了本书的意图。但是,由于会计概念对于测量公司证券的预期收益和
风险都十分重要,因此我还要讨论几个关键性问题。
首先,外部财务报表的目的是什么?在我看来,外部财务报表的
目的是为股东提供信息。可能有人认为,财务报表还应该为公司员
工、供应商以及债权人提供信息:员工根据财务报表评估自身人力资
本投资于公司的风险与收益,供应商根据报表评估与公司做生意的风
险与收益,而债权人则根据报表评估公司的违约风险。但我认为,既
然股东是公司所有者,他们通过影响公司股价从而间接为公司做出资
源分配决策,因此,财务报表的主要使用对象是公司股东。虽然财务
报表还有其他目的,但其首要目的是帮助股东判定公司股票价格。这
一观点与金融经济学中的基本观点“企业应为股东谋取利益”一致,也受到法律的认同。在实践中,虽然员工、供应商以及债权人能获取
有关公司的其他信息,但为股东编制的年报(包括资产负债表和损益
表)则是他们获取信息的重要来源,对大型上市公司尤其如此。
企业要履行为股东提供信息的义务,一个办法就是将每个员工全
年的工作情况拍摄下来,集合起来寄给每位股东。这样,股东就能没
有偏差地全面了解当年的实际情况。但是,这种做法显然是很荒谬
的。还有另一种极端的做法,就是企业每年年末只给股东提供一个数
字——企业对自身股价的估计值。这种方法也同样不可取,因为企业
没有足够的信息对股价做出准确的评估。正如哈耶克(1945)指出
的,影响公司股价的因素通常广泛分布于整个经济体中,没有哪个小
部分个体甚至企业所有员工拥有足够信息对公司股价做出有效的估
计。撇开信息量不说,即便你拥有足够的信息,用什么方法将信息糅
合进股票价格也不明确,更不能指望企业会知道如何做。企业可能出
于利益的关系,故意过高估计股价,以此来操纵企业从投资者手中获
得的资源或者调整管理层的激励报酬方案。另外,企业还面临一个约
束,不能发布那些削弱他们与其他企业相互竞争的动力信息,尽管这
种信息可能有助于股价评估。因此,会计的难点就在于找到一种折中
的办法,既要能概括一年中发生的事情,同时又不能泄露任何重要的
信息,不能指望企业完全诚信,亦不能损害企业的竞争动力。从帕乔利开始人们就一直在思索解决上述难题的办法,最终想出
的办法就是提供两张财务报表:资产负债表和损益表。第一张表,资
产负债表,就像一张快照,捕捉了公司在某一特定时点的相关信息。
第二张,损益表,像一部电影,演示了企业的资产负债表是如何从前
一个时点变到另一个时点。资产负债表反映了所有导致资产发生变化
并相应引起负债或股东权益发生变化的交易(有时是某些权益与负债
的互换或者一项资产换成另一项资产)。这让我们得到复式记账法的
基本原理、赫赫有名的会计等式:
资产=负债+所有者权益 (1-1)
任何交易都有两方面影响,如同时增加资产与负债,或增加某类
资产的同时减少另一类资产,最终保持等式成立。通常资产被划分为
三类:第一是流动资产,包括现金、应收账款、存货以及预付费用
等;第二是长期有形资产,如厂房、设备等;第三是长期无形资产,如研发费用的资本化价值以及著名品牌价值。负债分为短期负债与长
期负债两类:短期负债包括应付账款、递延税收与短期债务;长期负
债包括长期银行债务、公开发行的企业债券等。所有者权益分为实收
资本与累积盈余两项。损益表将各项费用扣减各项费用后得到利润,这部分利润是企业在两张资产表所在时点构成的时段内获得的利润。
如果用利润除以发行的股份总数,就得到每股收益(EPS)。企业财务
报表还会单独报告发放股利占利润的比例,用以计算每股股利。
如果投资者只想用一个数据来说明问题,那他可以只看每股收益
指标。该指标是会计师对两张资产负债表时点之间企业股价本应变化
多少的一个估计(加上股利)。也就是说,假设S t-1和S t分别是在时
点t-1和时点t的股价,D t是每股股利,而X t是两时点之间报告的每股
收益,则
(S t+D t)-S t-1=X t (1-2)
如果会计师与股票市场都是理性的,那么股票价格的变化应该正好满
足这个等式。
而且,使用上述EPS等式以及所谓的净盈余会计关系(假定没有新
增实收资本),则
Y t=Y t-1+X t-D t (1-3)我们可以证明每股股价S t等于对应的每股账面价值Y t。我们从时
点0企业的初始状况开始,S 0=Y 0,账面价值Y 0为实收资本。我们可
以得到如下递归等式:
事实上,即便市场是有效运转的,大多数公司的市场价值与账面
价值也不相等。虽然我们有理由责怪会计师们,他们处理账务时也是
左右为难。比如,有时候企业在卖出产品之后数月才收到货款、支付
费用,而有时候企业在产品卖出去之前就提早收到现金或支出现金。
如果简单地把当年发生的所有交易都记为收入或者费用,会让人产生
误解。而会计的“匹配原则”要求只有当年已经销售出去的产品所带
来的销售收入以及生产这些已销售产品所产生的费用才能记入该年的
损益表。与当年已销售产品不匹配的现金流入或现金支出则以某种形
式进入资产负债表,通常等到来年产品销售出去之后再进入下一年的
损益表。这称为“权责发生制”,与“现金收付制”不同。现金收付
制用现金流出匹配现金流入,而不是用费用匹配收入。会计师们面临
这样的权衡:使用现金收付制能提高报表的准确性,而使用权责发生
制能提供更为有用但可能不太准确的信息。对于编制外部财务报表而
言,会计师们更倾向于权责发生制。
举个简单的例子,资产负债表上之所以有存货一项就是因为存在
匹配原则。存货反映的内容可能是已经采购但尚未投入生产的原材料
或者尚未销售给顾客的产成品。这样,如何记录存货的成本又是一个
会计问题。比如,如果企业同一种存货是分批以不同的价格采购进
来,那么那些已制成产成品并销售出去的部分存货应该如何计算费用
呢?一种方法是假定先采购的存货先使用,即先进先出法(FIFO);
另一种方法是假定后采购的存货先使用,即后进先出法(LIFO)。
再看个稍微复杂点的问题。假设企业购买了一台使用寿命较长的
生产设备,该设备将在较长一段时间内慢慢损耗,最终技术上将过
时。根据匹配原则,企业需要确定每年为了生产那些已销售的产品,设备损耗了多少。虽然我们知道设备的原始采购成本,也知道几年后
如果将设备售出能获得多少收入,但我们很难找到一个完美的方法来
确定该设备每年具体的折旧率。因为没有交易能证明折旧费用的具体
金额。于是会计师们以他们最中意的方式解决这一难题。他们假定设备每年都以某个固定的折旧率折旧,当然这个折旧率取决于设备的类
型。这种简单的方法称为直线折旧法。如果设备使用10年,那么每年
记入设备费用的就是采购成本的10%。不过,直线折旧法并不能准确反
映设备的折旧情况,往往设备在最初使用年份折旧较快而之后折旧较
慢,于是会计师们有时采取加速折旧法。一方面,会计师们希望能给
企业一定余地让它们能更好地匹配收入与费用,但同时,他们又担忧
如果弹性过大,企业可能会借此误报(通常是夸大)收入。所以会计
师们总是努力找到平衡点。也正是因为这种平衡行为使得会计工作更
加富有趣味,而所谓的常规也不再一成不变。
尤其复杂的是如何分配研发费用、营销费用与广告费用。应该先
将它们资本化再慢慢转为成(摊销)费用呢,还是应该立即记为费用
呢?要回答这一问题,我们需要解决一个非常复杂的难题:这些费用
到底在多大程度上影响那些不在费用发生当年而是在随后年份销售的
产品所产生的收入与费用?
上述例子引出了另一个会计原则:由于股东将使用会计信息预测
未来的收入与费用,因而财务报表需要让股东能非常轻松地判断哪些
收入与费用是由于企业持续经营产生的,哪些是因为某一次特殊情况
所产生的。为了实现这一目的,企业的利润与损失通常被划分为两
类:一般损益与非经常性损益。非经常性利润来自预期之外的企业资
产与负债价值的变化。我们有必要区分如下三种非经常性利润:①由
非企业掌控因素变化带来的利润,如利率波动会影响企业负债的现
值;②企业在日常经营之外的有意决策所带来的利润,如企业决定持
有日元现金而不是美元现金;③由于事后对早期会计报表的更正而带
来的损益,如由于产品需求发生变化而导致存货滞销,这部分存货不
再用于销售因而给企业造成损失。遗憾的是,最后一类往往说明企业
在前几年没有很好地遵守匹配原则。不过,出于估值的目的,我们还
是越早知道这类的坏消息越好。
另一个要解决的会计难题是应该简单报告已实施交易的结果呢,还是不断修正这些结果以反映市场价值的变化呢?例如,一家水果企
业最重要的资产就是它在1900年以100万美元购置的一块地皮。在购置
之初,资产负债表上显示资产价值100万美元。过了一个世纪,随着旅
游业的飙升,该地皮的价值已经逐渐上升为1亿美元。假设现在企业其
他资产的价值与该地皮相比已经微不足道。如果企业的资产负债表依
然显示该土地的价值为100万美元,那么股东就无从得知如果企业将土
地卖掉就可以获得高额收入。显然,企业需要每年都更新土地的市场价值,价值的变动以非经常性损益列示。这样,资产负债表上的资产
和所有者权益都将发生相应变化:土地的价值为1亿美元,同时所有者
权益增加9900万美元。不过,市场会计价值法在解决一个问题的同时
又带来一个新问题:既然土地还没有卖出去,企业又如何知道它到底
价值几何呢?虽然这种不确定性可以通过多种方式降低,但没有办法
完全消除。如果不确定性不能消除,那么以市场价值为基准的记账法
就不如以实际交易为基础来得准确。股东也希望区分未售出土地的未
实现收入与已售出土地的已实现收入。另外,只要土地尚未售出,不
同专家对其市场价值就会有不同的看法。股东应该相信哪个专家呢?
尤其是当企业管理层有动力夸大土地价值时,股东是否能够相信企业
聘用的专家呢?
公认会计准则(GAAP)为这一问题提供了全面回答:根据资产市
场价值的不确定性,某些资产和负债可以按照市场价值重新评估,而
其他资产则不可以。其他资产,如资本设备,既不是按市场价值也不
是按成本价格进行评估,而是严格按照某些设计好的折旧处理方式来
估计资产价值的可能损失。
导致前文描述公司股价与收益关系以及每股市场价格与账面价值
关系的等式不成立的原因有多个与估值相关的问题,上述例子只是其
中几个而已。最重要的原因可能来自行业竞争的结构性状况。在许多
行业,企业有能力建立垄断优势或寡头垄断优势,这些优势不受企业
账面价值影响。通常当产品需求尚未扩大时,只有少量企业会进入该
行业。这一现象使得先动优势非常明显。例如,曾开发出最受欢迎个
人计算机(PC)操作系统的微软公司曾为我们很好地展示了如何利用
自己独一无二的优势来主导PC软件应用行业。然而,即便微软的实体
资产是按市场价值记入财务报表,读者也无法从微软的所有过去交易
以及财务报表中预测到它的市场价值与账面价值的高比率。企业市场
价值与账面价值的差异不仅反映了企业当前极高经营利润率,而且还
体现了企业拥有在将来能带来高额利润的投资机会,这种投资机会是
其他不具备微软垄断优势的企业所不具备的。而股票市场不会自动等
待利润的到来,而是早就将这些利润反映到股价中;市场会预期企业
未来利润,从而导致企业的市场价值与账面价值出现重大分歧。
基于上述观点,金融学家把高MB(市场价值账面价值)比率的
企业称为成长型企业,而低MB比率的企业称为价值型企业。投资者可
以投资共同基金,某些基金专注于成长型股票,而某些基金专注于价
值型股票。我们希望上述讨论已经清楚解释了企业账面价值与市场价值出现差异的多种原因,但是用于区分成长型股票与价值型股票的MB
比率并不是完美的。
从历史角度来看,用于度量业绩的会计报表侧重于企业盈利水
平,这是一个收益指标。但是,从马科维茨(1952年3月)和罗伊
(1952)开始,金融经济学家们就开始认为,除了收益,业绩应该还
包含另一方面,那就是风险。虽说现在会计制度的设计并不是为风险
考虑(可能需要重新设计,使得风险度量更加容易),现代财务报表
仍十分有用。例如,根据连续的财务报表,我们可以得到每股经常性
收益的时间序列,据此算出收益的方差,而收益方差则是衡量股票投
资风险的一个独立指标。然而不幸的是,不少企业都想尽办法,利用
匹配原则的灵活性调整各期收入或费用,从而稳定收益波动,使得风
险看起来似乎较低。
用财务报表测量风险的常用方法为比率分析法。例如,最常见的
流动资产对流动负债比率就是衡量企业违约风险的硬性指标。息税前
利润(EBIT)与年利息额之比是违约风险的流量指标。长期资产对短
期资产比率反映了企业的流动性和估值风险,因为短期资产的流动性
较高,其价值的不确定性较低。虽说企业股票的风险来自多个方面,有企业内的因素亦有企业外的因素,但就企业内而言风险主要有三种
来源:①收入来源的分散化;②经营风险;③财务风险。
现在的财务报表本身并不能提供企业分产品或分行业的收入信
息,来帮助投资者了解企业分散化经营程度。投资者只能从报表附注
或者其他渠道如企业发行证券之初的注册报告中寻找此类信息。
经营风险可以定义为固定成本与变动成本之比。比率越高,企业
利润对收入变化的敏感程度就越高。虽然损益表并没有直接区分固定
成本和变动成本,但依据成本的种类就可以在某种程度上对成本进行
区分,而且将各项费用与收入进行时间序列的回归分析就可以判断哪
些成本是固定成本,哪些成本是变动成本。
反映企业财务风险的常见指标是负债与权益之比,二者都使用账
面价值。负债对权益比率越高,企业的杠杆越高,则企业线下利润对
息税前利润变化的敏感程度就越高。不过,权益的账面价值往往并不
反映权益的市场价值;而负债的账面价值与市场价值则较为接近。而
且,我们随时都可以根据股票市场股价的变化获得权益的市场价值。因此,金融经济学家喜欢用负债的账面价值对权益的市场价值之比来
度量财务风险。
然而,这种度量财务风险的方法也并非轻而易举。显然,作为前
提条件,交易必须归类到负债或者权益。出于度量财务风险的目的,负债的本质来自于企业承诺支付的固定偿还额。即便企业偿还了所有
债务,债务所有者也不能分享企业成功的好处。而权益则不同,权益
没有支付义务,但在企业偿还所有其他人(包括雇员、供应商、债权
人以及政府)之后,企业所有的剩余都归权益所有者所有。正是因为
拥有“剩余索取权”,企业的盈利能力将直接增加所有者权益。有些
证券,如优先股、可转换债券以及员工股票期权,属于混合证券,既
有负债的特征又有股票的特征。如何对它们进行划分是个难题。
一致性是另一会计原则:不同企业处理日常经济本质类似交易的
规则设计应该不影响对企业收益与风险的比较。1994~2005年美国发生
的针对员工股票期权的争议就很好地说明了一致性问题。假设有两家
类似的企业A和B,不同的是企业A只使用现金支付员工报酬,而企业B
则只使用股票期权,最初为平价发行的期权。为了使案例简单化,我
们假定两家企业从员工手中获得相同的服务。自然,企业A将现金报酬
费用化,那企业B应该怎么做呢?如果按照标准做法企业B不将股票期
权作为费用处理,那么它的利润就会较高,尽管从经济角度来看它和
企业A做着相同的事情,而且企业B的业绩也并不优于企业A。因此,一
致性原则要求企业B在授予期权时就要确定期权的市场价值而且将其作
为费用处理。
处理租赁资产的例子很好地说明了实现一致性原则的困难。设想
有两家类似的企业:企业A借钱购买了一幢大楼;而企业B则是租赁了
相同的建筑。在企业A的资产负债表上,会计师们通常将大楼的购置成
本作为资产入账,同时增加相应的负债。通过这种方式,大楼的添置
提高了企业的负债对权益比率以及负债对资产比率。而在企业B的资产
负债表上,如果租赁期比该大楼的全部寿命周期短,那么租赁资产的
价值就不会出现在资产负债表上,它只以租赁费用的形式影响企业的
损益表。按照这种方式,企业B的负债对权益比率以及负债对资产比率
都不会发生任何变化,因而看起来它的财务风险似乎低于企业A。这种
处理方式迥异的主要原因在于两种交易的法律实质大不相同。企业A拥
有大楼的所有权,而企业B却没有。但是,从财务分析的角度来看,这
只是形式的差异,经济本质并没有什么差异。如果金融经济学家熟悉
租赁,他会这样理解租赁:其实企业B与企业A的区别不过是企业B借的是整幢大楼而不是现金;它定期支付租赁费用(经过折旧调整后的)
而不是利息费用;而且企业B最终将偿还大楼,就像企业A也要偿还借
款一样。如果遵循一致性原则,企业B就应该像企业A一样处理租赁业
务,使得两家企业的负债权益比一样。一种方法就是企业B将租赁建筑
物的价值借记资产,同时贷记相同数额的负债,说明企业有义务“偿
还”该“借来”的建筑。
上述做法尽管听起来很合理,但进一步分析就会显示实现一致性
原则是多么费力的一件事。按上述方法处理租赁意味着资产并不是按
照法律所有权来界定,而是定义为被企业使用并带来收入的事物——
企业B并不拥有该幢大楼,但企业用其获得收入,因而从这种意义上说
租来的大楼构成企业B的资产。现在,这个一致性目标的确为我们带来
困扰。设想一下:两家企业都使用了总部大楼外的街道,员工每天上
下班都使用该街道;当员工出差时他们还使用了飞机的座椅;如此等
等。如果遵循一致性原则,这些街道、飞机座椅等都应该出现在企业
资产负债表上。理论上,金融经济学家希望企业这样做。但我们再比
较如下两家企业:一家企业通过债务融资自己买下了航空公司和道
路,而另一家企业则是使用别人提供的道路和飞机座椅。如果再使用
一致性原则比较这个极端例子,显然很不实际。
我们不应该过于夸大设计完美会计准则的重要性。外部会计报表
只不过是人们获取企业信息的一种渠道。某些个人,如专业证券分析
师,专注于研究某个行业,他们大量的时间都用于评估该行业的上市
公司。因此,即便会计准则出现错误,也只是我们了解企业基本信息
的成本增加而已,市场仍会很好地给企业股票定价。例如,许多企业
管理人员认为,由于将股票期权费用化会降低每股收益,一旦改变会
计处理方式,它们的股价会下跌。但是,市场有其他方式了解到企业
的期权计划,因而更可能出现的情况是企业股价不会受到会计方式变
化的影响。1654年
布莱斯·帕斯卡(1623年6月19日—1662年8月19日) 出版了
《 论 算 术 三 角 形 》 ( Traité du triangle arithmétique avec
quelques autres petits traités sur la měme matière)。同年,与皮埃尔·费马(1601年8月17日—1665年1月12日)写就《与费马在
概率理论方面的通信集》(Correspondence with Fermat on the
Theory of Probabilities),见《西方世界的伟大著作:帕斯卡篇》
( Great Books of the Western World : Pascal ) ( Franklin
Library,1984),pp.447~487。
帕斯卡三角形、概率论、点数问题、帕斯卡赌注
最早对组合问题的研究似乎始于印度 1。大约在公元1150年,婆什
迦罗就认识到了从j个数中取出n个数的组合数为n![j!(n-
j)!]。早在1265年,阿拉伯数学家图西就知道了二项展开式
(a+b) n的系数计算以及如何在三角形中排列展开式系数。中国数学
家朱世杰1303年出版的《四元玉鉴》也讲述了二项展开式的计算,该
书的扉页后来广为流传。法国的马林·梅森(1588—1648)在1636年
就懂得了组合恒等式与展开式系数之间的对等关系。
帕斯卡虽然不是算术三角形的发明者,但他首次著文将组合数
学、二项展开式系数与三角形阵列这三者联系起来。由于帕斯卡对三
角形的特征进行了详细深入的探讨,因而从此以后人们将三角形阵列
称为帕斯卡三角形。值得指出的是,在论述算术三角形以及点数问题
时,帕斯卡并没有直接使用现代概率学的概念,甚至没有用过概率一
词。相反,他用的是组合数学语言,比如在多次试验中某某事件发生
多少次。因此,后文其实是我用现代化的语言对帕斯卡的研究进行的
重新表述。
帕斯卡三角形以1作为首行开始,接下来各行的每位数字等于上一
行位于它上方两个数字的和。帕斯卡指出,三角形具有许多令人惊讶的特征。例如,如果把首
行称为第0行,那么第n行的数字正是二项展开式(a+b) n的系数。而
第n行左手从0开始第j个数值正好等于n![j!(n-j)!]。
点数问题对概率论的发展至关重要,尤其是运用到机遇游戏(投
资)中。我们回忆一下该问题的基本形式。两人各下一定赌注,谁先赢到n点谁赢得赌注。每得一点都能获得一定奖励,而每轮两人输赢的
概率是一样的。如果当第一个人赢得x
人决定停止比赛,那么此时两人各自应该分得多少赌注?
帕乔利(1494)曾提出,假定两人各下注28个金币,n=6,且两
人的点数为(x,y)=(5,3),此时比赛叫停。帕乔利认为,最公平
的分法就是按照两人所得点数的比例分配金币。在这里,金币总数为
56个,那么第一个人分得35个金币,第二个人分得21个金币。意大利
数学家卡当,亦即有名的罗拉莫·卡达诺(1501年9月24日—1576年9
月21日)曾在1663年出版《论机遇赌博》(Liber de ludo aleae)。
后来亨利·古尔德提出了一个更复杂的解决办法。 [12]他认为应该按
照还没有结束的新比赛的结果来分配赌注。以帕乔利的例子来说,我
们可以设想一个A和B两人的新比赛。如果在B赢得3点之前,A先赢得1
分,则A赢;否则,B赢。那么在这个新游戏中,两人各自对赌注的贡
献是多少?卡当总结说,A投入3×(3+1)=12个金币,B投入1×(1
+1)=2个金币。这样,如果初始赌注为56个金币,那么A应该得到
56×(1214)=48个金币,而B得到56×(214)=8个金币。
帕斯卡三角形
帕斯卡三角形说明了二项树中的再组合问题,在二项树每一个节
点的数字等于上一排两个节点数字之和。更为一般的非再组合二项树
最早由波菲利(大约在公元234—305)推广开来。他是新柏拉图派哲
学 家 , 在 他 的 著 作 《 范 畴 导 论 》 ( Introduction to the
Categories)中用二项树说明了亚里士多德在范畴方面的逻辑论点。
在这个二项树中每一个范畴集合都被分为两个互斥的子集。例如:在帕斯卡三角形中的数字关系的数量开始是无穷尽的。甚至斐波
纳契数列也包含在其中。你是否能发现呢?从左边开始,把一直延伸
到右上角的对角线上的数字相加。那么就有:1=1,1+1=2,1+2=3,1+3+1=5,1+4+3=8,以此类推。
帕乔利和卡达诺的方法都不正确。该问题最终在帕斯卡与费马的
一次著名通信(1654年)中得到解决,此次通信被认为是现代概率论
的发端。他们提出了数学期望的思想并假定每位参与者获得的金币为
倘若比赛尚未结束的情况下他们各自能得到的金币期望值。
费马的方法只需要数数A能获胜的方法或路径个数以及B能获胜的
路径数。在两位选手得分(5,3)情况下,接下来可能的结果为
(a a a)(a b a)(a b b)(b b a)
(a a b)(b a a)(b a b)(b b b)
其中,a表示第一个选手得一分,b表示第二个选手得一分。加粗
的结果意味着第一个选手赢得了比赛。既然在8个可能的结果中有7个
是A赢,那么A就应该得到49个金币,而B得到7个。
帕斯卡提出了另一种类似的解决办法,他使用的是反向递归动态
规划方法。帕斯卡首先问到,如果在双方得分为(5,5)时比赛叫停。由于A
和B两人都有平等的机会赢得56个金币,那么他们每人期望得到的是28
个金币,赌注是平均分配(28,28)。从这儿往后推,如果得分为
(5,4),再比一轮的话,那么一半的可能是(6,4),赌注分配为
(56,0);另一半的可能是(5,5),这种情况已经阐述,赌注分配
为(28,28)。因此,如果得分是(5,4),A得到(12)×56+
(12)×28=42个金币,B得到(12)×0+(12)×28=14个金
币。再往后推一轮到得分为(5,3)的情况,同样的道理可以得到,A
分配(12)×56+(12)×42=49个金币,B得到(12)×0+
(12)×14=7个金币。 2
帕斯卡还被誉为决策论的创始人。在他的《思绪》(Pensées)一
文中 [13],帕斯卡描述了他著名的“赌注”。他对是否相信上帝的分
析十分缜密,让人觉得就应该相信上帝的存在。他说,假设有两种相
互排斥的可能性。第一,如果世上没有上帝,那么相信上帝或者不相信上帝都无关紧要。第二,如果真的有上帝,那么相信上帝会为你带
来永生于天堂的无限幸福,而不信上帝则带来葬身于地狱的无尽痛
苦。这样,即便你主观地认为存在上帝的概率微乎其微,但只要这个
概率大于零,那么你相信上帝所获得的期望收益将会是无穷大。当
然,我们现在知道帕斯卡的推理存在严重的问题,因为他的结果取决
于他对现实世界可能状态的判断。比如,他忽略了另外一种可能,就
是即便存在上帝,信奉者也可能被送进地狱,因为没有人有足够的信
息判断他是否真的相信上帝;而怀疑上帝存在的人,在确定的信息下
拥有正确的观点从而可能上天堂。
尽管帕斯卡成绩显著,但还称不上是第一位决策理论家。在更早
的时候,犹太法典《塔木得9q》(Kethuboth 9q)就提出,男人不能
因为妻子婚前的性行为而与妻子离婚。原因在于,有可能是由于该男
人的关系而使妻子发生了婚前性行为;即便不是前一种情况,妻子也
可能是在并不情愿的情况下发生婚前性行为。总的来说,四种可能情
况中只有一种值得男人与妻子离婚,不值得离婚的情况占了多数,因
而法律上不允许。帕斯卡赌注可能是“施蒂格勒取名法则”的又一例
证。因为在公元303年阿诺庇乌在其著作《反对异教徒》(The Case
against the Pagans)中(第2卷第4章)就描述过类似的选择。
作为现代概率论产生的一个重大特征,帕斯卡也许是不自觉地同
时运用了概率论的二元性:一方面,用概率来解释类似于抛硬币以及
赌博游戏等物理过程。在这类过程中,概率可以无争议地确定(客观
概率),犹如我们在点数问题中所看见的。另一方面,还可以用概率
来解释不可重复事件。在这类事件中,人们对事件发生的概率大小往
往存在较大争议(主观概率),犹如我们在帕斯卡赌注中看见的。因
此,有人如萨维奇(1954)在《统计学基础》一书中就提出,利用本
适合于非重复事件的主观概率使得人们无法在备选方案中做出理性选
择。但是萨维奇的分析只在一种情况下成立,即针对备选方案的打赌
是切实可行的,决定打赌结果的事件是可观测的。比如,我们就人死
之后的结果进行打赌就是有问题的:即便相信死后没有生命的一方获
胜,他也没办法在死后亲自接受赌注。
在20世纪后半叶,数字计算机对投资理论的进一步发展起到至关
重要的作用。不管是利用数据库进行经验验证,还是通过数值分析解
决数学问题,都需要计算机的帮助。我们其实在相当长的时间内使用
了简易计算器,如公元前3000年人们使用的算盘。计算尺大约在
1630~1632年就发明出来。在1642~1644年,为科学做出诸多贡献的帕斯卡当时只有20岁左右,他就成功发明了第一台数字计算机。帕斯卡
的计算机是通过转动转盘来输入数字,通过齿轮来完成加减法。当你
拨动数字时,里面的齿轮就会移动。运算结果显示在键盘上方的窗
口。我们可以在巴黎的法国国立工艺学院看到帕斯卡签名的1652年版
计算机。如果你到伦敦比较方便,那么你可以在南肯辛顿的科学博物
馆看到该计算机的复制品。1657年
克里斯汀·惠更斯(1629年4月14日—1695年7月8日),写了一本
名为《机遇赌博的规律》(De ratiociniis in aleae ludo)
(Calculating in Games of Chance)的小册子,首次以拉丁文形式
出 版 在 1657 年 弗 兰 斯 · 范 · 斯 库 坦 迪 编 写 的 Exercitationum
mathematicarum libri quinque的附录中,随后于1660年以荷兰语出
版在Van rekiningh in spelen van geluck中;后来,雅各·伯努利
(1713)对惠更斯的著作进行了注解;截至2004年3月6日,我们可以
在 互 联 网 上 看 到 该 书 的 英 文 翻 译 版 , 网 址 为
www.stat.ucla.eduhistoryhuygens.pdf。
概率论、期望、套利、状态价格、赌徒破产问题
在1657年之前,惠更斯就已久负盛名,是他发现了土星光环和土
星最大的卫星“泰坦星”(土卫六),是他首次注意到了火星表面的
斑纹。他还在1656年发明了摆钟。紧接着,惠更斯又在1657年出版了
他第一篇有关概率的著作,这是一篇16页的论文,在文中他阐述了期
望的特征。虽说他的论文赫赫有名,但他与帕斯卡(1654)、帕斯卡-
费马(1654)一样,仍然没有使用现代概率的概念。而且,尽管惠更
斯的结果可以用现代概率与期望的概念来解释,但他脑子里有别的想
法。对他而言,期望就是赌博中参与者应该付出的赌资。可以说,是
投资学的某个问题推动了现代概率论的产生(而不是人们猜想的概率
论推动投资学发展),这是思想史上令人称奇的逆向发展之一。
根据伊恩·哈金对惠更斯命题的评论 [14],我们看看如下的抽奖
游戏。游戏参与方有P1和P2两人。由游戏主持方抛掷硬币,由P1来猜
结果。如果P1猜对了,P1将获得X>0的奖金,P2则一无所获。我们将奖
金分配写作(X,0)。如果P1猜错了,P1将一无所获,P2则获得X>0的
奖金,即奖金分配为(0,X)。惠更斯有个隐含假设:参与者交换序
列并不会改变各自得到的奖金。因此,在这个例子中,奖金分配(X,0)的价值应该等于(0,X)的价值。接着,他又提出,如果每个参与
者支付价格(或者赌资)P=X2,那么该游戏是公平的(假设1)。这
跟我们现在所说的套利原理是一致的。设想,如果P>X2,那么游戏主
持方肯定盈利,因为他的总收入大于他提供的奖金:2P>X。而如果
P
损。接着,惠更斯将游戏规则修改了一下,让获胜方同意支付K作为对
输方的安慰奖,0
个人得到的奖金或者为X-K,或者为K,机会均等。惠更斯假定,这一
修改并不改变参与者支付的游戏价格P(假设2)。惠更斯还假定,奖
金分配结果相同的两种抽奖游戏的价格必须是一样的(假设3)——该
假设我们现在称为“单一价格法则”。
惠更斯以三个命题开始:
命题1:如果参与者获得A或B的机会均等,那么他的期望值为
(A+B)2。
命题2:如果参与者获得A、B或C的机会均等,那么他的期望值为
(A+B+C)3。
命题3:如果参与者获得A的机会次数为n 1次,获得B的机会次数为
n 2次,那么他的期望值为(n 1A+n 2B)(n 1+n 2)。
命题1和命题2针对等概率状态。按照现代词汇解释,命题3涉及了
我们现在讲的概率不等情况下的期望概念。我们可以看到比率n 1(n
1+n 2)≡p,于是期望等于pA+(1-p)B。
在300多年后的今天,我们认为命题1理所当然是成立的。可是在
1657年,情况可不是如此。
对惠更斯命题1的证明
假设两个参与者参加一项公平抽奖游戏I,奖金为A+B(A
根据假设1,要使游戏公平,参与游戏的价格必须等于(A+B)2。再
假设,获胜方必须向对方支付一笔安慰奖A。因此,不管哪个参与者,只要他获胜,他就得到(A+B)-A=B;如果他输了,则得到安慰奖A。
可以看出,这个抽奖游戏的奖金分配结果与另一公平游戏II——参与
者有均等机会获得A或B(假设2)——的分配结果是一样的。既然游戏
I和游戏II的分配结果一样,那么他们的价格也必须是一样的(假设
3)。即游戏II的公平价格等于游戏I的公平价格:(A+B)2。命题1
得证。命题2的证明如下:现在有三个参与者P1、P2和P3。既然游戏是公
平的,那么如果P1赢得所有赌资X,他得向P2支付B,向P3支付C。因
此,如果P1赢,他得到A≡X-(B+C)。同样,如果P2赢,他向P1支付
B;如果P3赢,他向P1支付C。这样,P1有均等机会获得A、B或C。P2和
P3也是如此,他们也有均等机会获得A、B或C。表1-1显示了这些结
果: 3
表 1-1
命题3进一步扩展了假设2。惠更斯现在提出一个有n 1+n 2个参与
者的抽奖游戏。每个参与者的赌资为X。游戏是公平的,因为总奖金为
X×(n 1+n 2),每个参与者获胜的机会均等。第一个参与者与其他n
1-1个参与者达成协议,如果他获胜,他将向每个人支付A;相反,如果
是他们中某人赢了,则得向他支付A。对于另外n 2个参与者,他答应赢
了后向他们每人支付B;如果他们中某人赢了,也向他支付B。接着,根据与前两个定理证明类似的道理,他证明了定理3。
令人惊讶的是,惠更斯脑子里的原概念是“价值”而不是“概
率”。把他的定理与现代金融联系起来,仿佛他是直接使用状态价格
π a和π b来思考估值问题(利率近似为零,因此r=1)。其中,出现
π a的概率为n 1(n 1+n 2),出现π b的概率为n 2(n 1+n 2)。
这样,抽奖游戏的价值为π a(A)+π b(B)。
在状态价格的解释中,同样出于套利的原因,状态价格π a和π b
的总和必须为1,而且两者都为正。然而,现代理论并没有接受惠更斯
的隐含假设,即在等概率状态中改变参与者序列并不改变游戏价值。也就是说,在现代理论中,机会均等的奖金分配(X,0)和(0,X)
并不等值。
按照现代观点来看,状态价格不仅反映概率,还反映了风险程度
与风险规避程度。我们知道,惠更斯隐含在假设1背后的观点——参与
者获得X或0机会均等的赌博的价值等于X2——并不一定成立。如果现
实中不存在另外一种奖金为0或X的反向赌博,那么惠更斯的观点就不
成立。根据惠更斯的假设,如果两类赌博都以相同数量存在于同一市
场,那么风险可以完全分散,赌博的价格应该等于期望收益。但如果
只存在一种赌博而另一种不存在,由于风险不能完全分散,赌博的价
格就可能高于或者低于期望价值,是高是低取决于其收益与其他可投
资项目的相关程度、赌博与对参与者而言重要的其他因素的关系以及
参与者的风险规避程度。或者,由于非赌博因素造成参与者的其他财
富在两种状态下不一致,那么这两种赌博的价格也会不一致。比如,如果在第一种状态下参与者的总体财富低于第二种状态,那么即便两
位参与者增加额外赌注,分配结果为(X,0)的价值也将高于(0,X)的价值(当然,根据前文说过的简单套利理论,不管两种赌博的价
格怎样,两者之和肯定等于X)。
突然想到一个现实生活中的例子,2000年爱荷华大学曾办过一次
总统选举赌博,获胜者可以拿走全部赌注。参与者可以出资P B,如果
布什当选总统,他可以赢得1美元;如果布什落选,他得0。参与者还
可以出资P G,如果戈尔当选总统,他可以赢得1美元;如果戈尔落选,他得0。如果我们忽略还有第三位候选人获胜的概率,套利原则要求两
种价格之和P B+P G=1美元。事实上,这只是个极度近似值。我们是
否可以像惠更斯那样将P B理解为布什当选的期望价值,将P G理解为戈
尔当选的期望价值呢?这可不一定。假如参与者预期布什当选总统时
的经济状况好于戈尔,而且参与者们都是风险规避型,那么戈尔当选
所增加的1美元的效用将大于布什当选增加的1美元。或者,参与者赌
布什赢而布什真的当选,那么参与者就无法获得如果他打赌戈尔而且
戈尔当选所能获得的额外1美元,他会因此遗憾。因此,下注布什或者
戈尔的价格不仅取决于主观概率,还取决于效用。最终,赌布什赢的
价格P B将略微低于布什当选的主观概率,而赌戈尔赢的价格P G将略微
高于戈尔当选的主观概率——不管怎样,两者之和都等于1。
利用3个基础命题,惠更斯证明了另外11个命题,提出但未解决5
个问题,其中有些问题是由费马提出来的。定理4至定理9针对的是当时帕斯卡-费马(1654)讨论的点数问题。而定理10至定理14则移至新
的领域。简单地说,命题10回答这样一个问题:一个人需要掷多少次
骰子才会掷出6点?惠更斯利用反向递归的方法解决了这一问题。掷一
次就能掷出6点的概率X 1=16,而不是6点的概率为56。掷两次能得到
6点的概率等于第二次得到6点的概率16加上第二次没有得到但第一次
得到6点的概率(56)X 1。即掷两次得到6点的概率为X 2=16+
(56)X 1。同理,掷三次能得到6点的概率等于第三次得到6点的概率
16加上第三次没有得到但前两次得到的概率(56)X 2。即掷三次得
到6点的概率为X 3=16+(56)X 2。继续推下去,我们可以得到掷k
次得到6点的概率为X k=16+(56)X k-1。根据该公式,我们不难
看出,当k=4时,掷出6点的概率在12至6711296之间[尽管惠更斯没
有解出该数列的公式,我们不难得到X k=1-(56) k]。
最后一个命题,命题14,他把这种递归方法再深入一步,用以分
析比赛轮数没有限制的情况。该定理回答如下问题:假如两位选手轮
流掷两枚骰子。如果A先掷出7点,则A赢;如果B先掷出6点,则B赢;
且由B先掷。问:A获胜的几率为多少?显然,A在第一轮就得到7点的
概率为636,而B在第一轮得到6点的概率为536。惠更斯建立了两个
联立方程。设A获胜的概率为p,那么B获胜的概率最终为1-p。每当B
掷骰子时,情况都和比赛刚开始时一样,A赢的概率都将为p。而每当A
开始掷时,A最终获胜的概率将大于p,假设是q。因此,根据定理3,当B开始掷骰子时,A最终获胜的概率等于:
同理,当A开始掷骰子时,A最终获胜的概率等于:
通过解联立方程,我们可以得到p=3161,即A胜败的概率之比为
31∶30。惠更斯在书中最后附上的5个问题是赌徒破产问题,最初由帕斯卡
提出:两位赌资相同的选手开始比赛。他们将依序进行多轮比赛。每
一轮,第一位选手获胜的概率为p,如果获胜他将从第二位选手的赌资
中拿走1个单位;相应的,第二位选手获胜的概率为1-p,获胜后他从
第一位选手的赌资中也拿走1个单位。一旦某位选手赌资输完,比赛就
结束。问:比赛最多出现n轮的概率是多少?
赌徒破产问题对日后随机游走与布朗运动的发展起了至关重要的
作用。按照现代术语来说,就是在两个吸收壁之间随机游走,其中一
个吸收壁显示第一位选手的得失,另一个吸收壁显示第二位选手的得
失。1713年,哈尔德(2003)在他与皮埃尔·雷蒙德·蒙特莫特的通
信中曾提到尼古拉斯·伯努利解答了这一问题:两位选手赌资不同,能进行多轮比赛。假设选手A的初始赌资为a,B的初始赌资为b;每轮A
赢的概率为p,B赢的概率则为q=1-p。那么,B破产的概率R(a,b;
p)(亦即A赢得所有赌注)的概率为:1662年
约翰·格兰特(1620年4月24日—1674年4月18日)出版了《对死
亡率表的自然与政治观察》(Natural and Political Observations
Made Upon the Bills of Mortality)(伦敦,1662年);再版于B.
本 杰 明 : 《 约 翰 · 格 兰 特 的 〈 观 察 〉 》 ( John
Graunt's‘Observations’),载于《精算学会杂志》,第90卷
(1962),pp.1~60。
统计学、死亡率表、期望寿命
继机遇赌博之后,投资领域首次领略到全新概率推理的好处。反
过来,在投资领域应用概率推理又进一步推动了概率论的发展,统计
学相关领域的发展也由此展开。在这部分的介绍中,我首先得解释人
们如何创建人类死亡率表以及这些表又是如何被用来确定人寿年金的
现值的(人寿年金的支付额取决于年金领取者的剩余寿命)。
进行人口普查的历史至少可以追溯到罗马共和国时期。著名的
《末日审判书》(Doomsday Book)则是多年之后才出现的人口普查清
册,是1086年英国人出于征税目的而编制的。不过,针对该书的数据
类型(其实所有数据类型都可以),格兰特(1662)编写了他第一部
出版的统计分析著作,成为我们知道的第一位统计学家。在当时,格
兰特的分析是独一无二的,就是放到现在他的统计模型亦是令人称奇
的高深。只是那时候人们还不知道用图形来表示时间序列或者横截面
数据,他只能用表格的形式来演示。
依据安德斯·哈尔德(2003)的描述,格兰特的分析是基于每周
搜集的伦敦人口重要统计量数据,数据的起始时间是1604年,某些数
据的时间截至1672年。 [15]和现代优秀的统计学家一样,格兰特因为
担心误差所以调整不合理的峰值,进行一致性检验并寻找支持性证
据。例如,为了计算伦敦的家庭数,他分别依据出生、死亡以及房子
数设计了三种计算方法。然后寻找有效方法来归纳这些数据。例如,他按照死亡原因总结了死亡人数(第2章)见表1-2:
表 1-2格兰特将每年死亡原因中固定的部分(“慢性的”)与变动的部
分(“流行的”)区分开来。他注意到许多居民对某些死亡原因过于
恐惧,因此他希望他的统计数据能让人们放宽心。他还用其他表格列
示了不同死亡原因随时间变化而变化的时间序列数据。尽管格兰特还
不能准确理解样本规模对降低风险的作用,但他已直觉地感受到当他
将样本按时间段(如按时代)进行划分后,趋势会越发明显。利用这
些数据,格兰特率先观测到男性和女性占人口的比率相当接近,而且
长时间稳定不变。他提出并检验了如下假设:在人口死亡相对较多的
年份,新生儿出生较少。
对随后概率论发展最为重要的是,格兰特首次尝试构建死亡率
表。为了制作该表,格兰特必须从数据中推断出总人口的变化以及不
同年龄段的死亡人数。由于他没有直接的相关信息,他想出了一个聪
明的办法,可以依据现有数据推算出来。表1-3就是格兰特最后得到的
死亡率表(哈尔德,2003,p.102):
表 1-3值得指出的是,在17世纪这种分析方法最初被称为“政治算
术”,随后被称为“统计学”。“统计”(statistics)一词的来意
是指搜集并分析与国事相关的事实(status为state的拉丁语)。
1669年克里斯汀·惠更斯和他的弟弟路德维希·惠更斯在格兰特
死亡率表的基础上进行了多项统计创新(这些结果后来出版于克里斯
汀·惠更斯的《拉普拉斯全集》)(Oeuvres Complètes,第6卷,1895年)。路德维希希望通过格兰特表格,根据一个人的目前年龄推
算出他的预期寿命。为了实现这一目的,他假定,在格兰特的观测范
围内,死亡概率的分布是相同的。哈尔德(2003,p.107)用表1-4表
述了路德维希的计算结果。
表1-4 路德维希·惠更斯的死亡率表表中变量x和l x数据直接取自格兰特的表格;d x是l x的一阶方
差;t x是各年龄段起点与终点之间的中点。假定各年龄段的死亡率分
布相同,那么t x就等于那些d x个死亡人数的平均寿命。路德维希推理
到,1822年是100个新生儿生存的总年份数:36个人平均生存3年,24
个平均生存11年,15个平均生存21年。依此类推,所有年份的总和为
1822 年 。 这 样 , 100 个 新 生 儿 在 0 岁 时 预 期 的 寿 命 为 1
822100=18.22=E(t 0)岁。同理,64个人在6岁时的预期寿命为171464=26.78=E(t 6)岁。如果已知某个人现在的年龄,我们用E(t
x)减去x就可以得到他剩余的寿命。克里斯汀当时40岁,路德维希推算
他的剩余寿命在17.5年和15年之间,也就是活,克里斯汀大约还能活
16.5年。
克里斯汀将弟弟的分析更深入一步。他把表格中第一列和第二列
的数字当成一个连续函数,这是最早的分布函数。他演示了如何计算
剩余寿命的中值而不是期望值。他还计算了在两个人A和B中,后去世
的那个人的期望剩余寿命。也就是说,如果T A(一个随机变量)是A的
剩余寿命,T B是B的剩余寿命,他计算的是E[max(T A,T B)]。首
先,对A剩余寿命T A的各个数字,他计算E(T B|T B≥T A)。接着他
对各种可能的期望寿命计算加权平均和,权重为T A的概率。这里我们
看到了条件期望概念的最早运用。如果定义T=max(T A,T B),我们
可以得到生存者的剩余寿命E(T)=E[E(T|T A)],这就是我们现在
说的迭代期望原则。1671年
约翰·德威特(1625年9月24日—1672年8月20日)出版了《人寿
年 金 的 价 值 》 ( Value of Life Annuities in Proportion to
Redeemable Annuities)(1671年用荷兰语出版);另见《保险史与
生命或有理论》(Contributions of the History of Insurance and
the Theory of Life Contingencies),载于《保险杂志》,第2卷
(1852年),pp.232~249。1693年
埃德蒙·哈雷 发表了《对人类死亡率的估计,数据源自布莱斯
勒城的出生与葬礼表,以及对年金价格的探讨》(An Estimate of
the Degrees of the Mortality of Mankind,Drawn from Curious
Tables of the Births and Funerals in the City of Breslaw;
with an Attempt to Ascertain the Price of Annuities upon
Lives),载于《皇家学会哲学汇刊》,第17卷(1693年),pp.596~610。1725年
亚伯拉罕·棣莫弗(1667年5月26日—1754年11月27日) 出版了
《论人寿年金》(A Treatise of Annuities on Lives);再版于棣
莫弗第3版《机遇论》的附加部分《对前版的补充、清晰与修正》;再
版于《美国数学学会学刊》(2000年),pp.261~328。
人寿年金、现值、死亡率表、状态价格、唐提养老保险
现在我们会认为概率论是为投资服务的,可是两者关系并不总是
如此。在早期,是因为我们希望依据死亡率算出现金流的现值,这才
出现了概率的思想。人寿年金是指保险公司每年支付年金领受人固定
金额,直到“被提名人”(通常就是年金领受人)死亡,年金领受人
的本金不偿还。社会保障就是人寿年金的现代大众版。比较常见的是
联合人寿年金,通常用于已婚夫妇或者全体船员,该年金只有在所有
人都存活的情况才继续存在。唐提联合养老保险与它相似,唯一不同
的是只要领受方有一个成员还健在保险金就继续支付。1653年,洛伦
佐·唐提向法国枢机主教马萨林推荐了一个政府集资计划,唐提养老
保险由此得名。唐提养老保险的一般协议是,一组参加保险者向基金
投入相同资金;然后每年他们共同得到一笔指定数额的年金,平均分
配。如果某一成员因为死亡而退出,就由余下成员分享年金总额。由
于年金总额保持不变,因而每人分得的年金增加。当只剩一个成员存
活时,他就得到全部年金。最后当所有参保成员都去世时,年金支付
就停止,基金的本金归基金发行者(如政府)所有。罗伯特·路易斯
·史蒂文森和劳埃德·奥斯本的中篇小说《入错棺材死错人》(The
Wrong Box)(1889)描述了唐提养老保险的另一种形式。参加保险的
初始成员共37人,直到最后只剩一人时该保险才支付保险金额,也就
是说,最后那个人获得全部初始资本与所有累积收益。
在公元前44年恺撒大帝被刺杀到公元前31年阿克提乌姆海战(历
史学家后来称之为罗马共和制灭亡以及罗马帝制开始的时间)的内战
期间,大约是公元前40年罗马颁布了法尔什德法(Roman Falcidian
Law)。根据该法,财产的法定继承人,通常是家中存活的长子,有权
继承该财产至少25%的价值。而非长子则通常是以人寿年金的形式领取
遗产,这样我们就需要知道年金的价值。人们用“收益年份”计量年
金,也就是我们现在说的“回收期”。比如,某笔年金每年支付100
元,收益年份为20年,这就意味着该年金的现行价格为100×20=2000(元)。从3世纪罗马法理学家乌尔比安那里,我们获得一张人寿
年金表。该表格清晰地显示出,年金的价值应该随着领受人年龄的增
长而降低(尽管可能存在人为的上偏,目的是保护长子的财产)。在
他的一份表格中,他指出,当领受人年龄为20时,人寿年金的价值为
30年收益年份;而当领受人的年龄到了60岁,人寿年金的价值只有7个
收益年份。我们现在知道了如何计算收益年份的价值上限。假设生命
是无限的、利息率为6%,那么年金的价值为10.06=16.67(元),即
年金在1个收益年份的价值为16.67。这是年金的最高价值,因为其他
任何事物的价值都低于无限生命的价值。
2000年,杰弗里·波伊特拉斯著书回顾了人寿年金的发展史。 [16]人寿年金始于17世纪,是政府用于集资的途径。年金普遍受到欢迎
的一个原因是它没有违反教会的高利贷法:由于年金购买者只收到利
息,本金并不返回,所以年金并不是债务。当然,年金的二级市场允
许购买者提前套现。那个时候,出现了更为复杂的收益年份概念。假
定P为一笔持续到未来某一固定年份年金的价格,X为年金每年的支付
额,利息率为r。收益年份t满足方程P=X[Σ k=1,2,…,t(1r
k)]。换句话说,收益年份就是让所有年支付额的现值等于年金价格
的时间。
虽然我们看到罗马人已经对年金被提名人的预期寿命进行了调
整,但该调整还比较粗糙。对预期寿命进行精确调整的是德威特
(1671)。在称得上是第一份对期权类衍生品的正式分析中,德威特
提出了一种方法,即基于被提名人的年龄来计算人寿年金的价值。按
照现行标准,他的方法不算精细,但他使用的是当时第一份死亡率
表。德威特假定,被提名人将根据下面的数据死亡。在每768个提名者
中:
在第一个50年中每6个月将有6人死去;
在接下来10年中每6个月将有4人死去;
在接下来10年中每6个月将有3人死去;
在接下来7年中每6个月将有2人死去。
假设复利利率为4%,对768个死亡时间,他一一计算了其对应年金
的现值,然后取算术平均值,即为年金的价格。德威特还指出,他的计算结果可能向下偏,这是因为存在我们现在所说的“逆向选择”问
题:选择购买年金的人可能相对比较健康,因而比同龄人更加长寿。
虽然我们的回顾更注重思想的发展,而不是写思想发明者的传
记。不过我忍不住想提一提,在1672年,也就是德威特出版他有关人
寿年金的经典之作一年之后,他就被荷兰的革命暴徒公开绞死。毫无
疑问,这是因为具有金融天才的德威特在担任政府大臣时太过耀眼。
德威特曾请教过约翰·范·瓦佛兰·郝德(1628年4月23日—1704
年4月15日)。郝德根据1495个实际购买过年金的人的死亡数据,自己
算出了年金价值。哈雷(1693)也设计了自己的计算公式。哈雷使用
了与德威特不同的数据,两人的计算公式却得到了相同的结论。但哈
雷构建了一个更为基础的解答方式。将于时间t终止的年金的现值为
X[Σ k=1,2,…,t(1r k)]。假设qt为年金领受人在第t年死亡的概
率,那么根据德威特的公式,人寿年金的现值为
相反,假设p t为年金领受人在第t年存活的概率。哈雷首先计算e
t≡p tr t,然后再利用这些分子价格计算人寿年金的现值:
证明:哈雷与德威特的公式是等同的
要从德威特的公式推导出哈雷的公式,首先我们要推出年金领受
人在第t年死亡的概率q t与年金领受人在第t年存活的概率p t二者之间
的关系。p t等于领受人在t+1,t+2,t+3…死亡概率之和。如果某人在
第t年还活着,那么他肯定是在随后某一年死亡。因此,在第t年还活
着的概率等于在第t年之后死亡的概率。设想一个具体的例子,年金领
受人在第4年死亡。因此:p 1=q 2+q 3+q 4
p 2=q 3+q 4
p 3=q 4
解上述方程,我们可以得到q 2=p 1-p 2,q 3=p 2-p 3(假设p
4=0,那么q 4=p 3-p 4)。进而,我们得到:
q t=p t-1-p t
该等式的直观意义是:领受人在时间t死亡的概率等于在时间t-1
存活的概率减去在时间t存活的概率。这两个概率产生差异的原因只能
是领受人在时间t死亡。
把上式代进德威特的公式:
将前几项展开看看:
该等式的直观意义是:只有领受人在时间t还活着,他才能在该时
间收到年金,因此时间t期望年金的现值等于p t(1r t)。而各笔年
金之和的现值就等于年金现值之和,这就是该等式的含义。我们可以将e t看成是在第t年你收到1元的现值,条件是当且仅当
你到那时还活着。按照现在人寿年金的说法,这个e t被称为“生存保
险”的价格。保险精算师们将生存保险定义为投保人必须在指定时间
内生存,才能收到的一定款项;如果投保人在特定日期之前死亡,他
生前将什么也得不到。养老保险的条件宽泛一些:不管投保人是否活
过指定日期,投保人都可以收到一笔指定的总数再加上一笔利息。只
不过,如果投保人提前死亡,他得到的收入会有所变化。一般地,在
等额分期支付情况下,如果投保人还健在,他通常会得到补偿。该类
保险可以分解为两部分:一部分是生存保险,一旦在指定日期之前投
保人死亡,该部分就取消;另一部分是投保人提前死亡时支付的条件
保险。
数学家棣莫弗(1725)也研究过人寿年金问题,推导出了单一人
寿年金、联合人寿年金、唐提式养老保险以及退休金等的“解析
解”。他的问题1(pp.265~266)针对单一人寿年金。为了得到解析
解,他假定,生存概率随着年龄的增长而呈等差级数降低:
假定生存概率呈等差级数递减,求某一特定年龄人寿年金的价
值。
根据哈雷的公式,棣莫弗假定p t=1-(tn),这里n可以理解为投
保人剩余寿命的最大值。例如,一位男性现在30岁;如果n=50,那么
他能再活一年的概率为p 1=1-150=0.98;再活两年的概率为p 2=1-
250=0.96;再活50年的概率为p 50=1-5050=0。根据这一假设,年金
的现值为
依据等比级数的特征,棣莫弗指出(式中r ≡r-1):棣莫弗还提供了联合人寿年金的结果(问题2,pp.266~268):
假定已知两笔单项人寿年金的价值,求基于两人联合生存期的年
金的价值。
假设两个年龄分别为x和y的人各自购买了人寿年金,保险合同明
确说明,在两个人有生之年每年向两人各支付1元。设两个人年金的现
值分别为A x≡Σ t( xp tr t),Ay≡Σ t( yp tr t)。再假设两
个人继续存活的概率随着时间而呈几何递减,则 xP t=P t
x, yP t=P
t
y。例如,对年龄为x的人,他再存活一年的概率为p x,存活两年的概
率为p 2
x,依此类推。棣莫弗证明:如果两人为独立个体,那么基于他
们联合生命的年金(即只要两人健在就支付1美元)的现值等于:
我们再具体看看该等式的推导过程。自现在年龄开始,两人再活t
年的概率为(p xp y) t,因而联合年金的现值为A xy=Σ k=1,2,…,∞(p xp yr) t。既然棣莫弗已经提出了这个问题,我们需要按照单
一人寿年金展开该等式。第一人单一人寿年金的现值为A x=Σ k=1,2,…,∞(p xr) t=(p xr)[1-(p xr)]=p x(r-p x)。同
样,第二个人年金的现值为A y=p y(r-p y)。解上述两个等式,再
将p x与p y的表达式代入联合年金A xy的表达式,即得到上述结果。
棣莫弗还考虑了一个唐提式养老保险问题(问题4,p.270):
假定已知两笔单一人寿年金的价值,不管是否谁先死亡,求两人
中较长寿者的年金价值。
无须特别假定 xp t与 yp t不依赖于t,棣莫弗证明了该年金价值
为A x+A y-A xy。很显然,两人中至少有1人在时间t还存活的概率为1-(1- xp t)
(1- yp t)。因此,唐提式养老保险的现值为Σ t[1-(1- xp t)
(1- yp t)]r t。把该式分解为三个部分,一部分为 xp t,一部分
为 yp t,另一部分为 xp typ t,就得到上述结果。
棣莫弗的问题7(p.272)由于“继承”产生的人寿年金的价值:
假设A拥有一笔年金,在A去世后B可以得到一笔人寿年金,求A去
世后B的人寿年金的价值。
同样无须特别假定 xp t与 yp t不依赖于t,棣莫弗证明了该年金
价值为A x-A xy。
同理,很显然,在第t年A已经去世而B存活的概率为(1- xp t)
yp t。因此唐提养老保险的现值为Σ t[(1- xp t) yp t]r t。把
该式分解为两个部分,一部分为 yp t,另一部分为 xp typ t,就得到
上述结果。1738年
丹尼尔·伯努利(1700年2月8日—1782年3月17日) 用拉丁文发
表了《有关衡量风险的新理论说明》(Specimen Theoriae Novae de
Mensura Sortis);后来由L.萨默翻译成英文并出版在《计量经济
学》第22卷,第1期(1954年1月),pp.23~36。1934年
卡尔·门格尔(1902年1月13日—1985年10月5日) 用德文发表
了《论不确定性在经济学中的角色》(Das Unsicherheitsmoment in
der Wertlehre),后由沃尔夫冈·绍尔科普夫在马丁·舒比克所编著
的《纪念奥斯卡·摩根斯顿数理经济学论文集》(Princeton
University Press,1967年)中翻译成英文。
风险规避、圣彼得堡悖论、期望效用、对数效用、分散化、韦伯-
费希纳精神物理学定律、有界效用函数
帕斯卡和费马(1654)在解决点数问题时假定赌博的价格等于它
的期望价值。惠更斯(1657)亦是在该假设基础上形成了完整的机遇
理论。而伯努利的经典之作(1738)则始于这样一个观点:由于风险
规避的存在,赌博的价格低于其期望价值。伯努利用圣彼得堡悖论证
明了风险规避的合理性。如果有机会让你抛掷硬币直到硬币第一次正
面朝上,你愿意为该机会支付多少钱呢?假如在抛掷第n次时硬币首次
正面朝上,你获得2 n美元。该赌博的期望价值为
虽然该赌博的期望价值是无穷大,但你愿意支付的价格肯定只是
有限数目,而且毫无疑问远远低于你的财富总和。因此,赌博的价格
肯定低于其期望价值。
为了解决该问题,伯努利提出每个人都是最大化其期望效用,伯
努利有时称为“道德期望”。伯努利还特别建议使用效用函数
U(W),该函数的特征是“任何幅度的财富增加所产生的效用与之前
持有的财产数量(W)成反比”,即:该方程的解为U(W)=a+b(lnW),或者将效用直接表达为logW的
递增线性表达式。这样的话,赌博的期望效用变为
该等式说明,个人最多愿意为赌博支付4个达克特。伯努利指出,是他的表弟尼古拉斯·伯努利(1687年10月10日—1759年11月29日)
首次提出了圣彼得堡悖论。尼古拉斯原来坚信期望价值是公平本质的
体现,可是悖论的发现打乱了他的信念,这让他非常苦恼。丹尼尔还
指出,早在他之前好几年,数学家加百列·克莱姆在1728年写给尼古
拉斯的一封信中就提出过自己的解法。
早于马科维茨(1952)和罗伊(1952),丹尼尔还提出风险规避
的投资者希望资产分散化:“……应该明智地将各种不同风险的资产
分散开来而不是将他们集中在一起。”第一个意识到分散化好处的人
并不是伯努利。根据犹太法典《塔木德》的建议,“一个人应该以三
种形式保存自己的财富:13存于房地产,另13存于货物,还有13存
于流动资产。”在《威尼斯商人》第一场第一幕,威廉·莎士比亚就
让安东尼说道:……我感谢我的财富。我的买卖的成败并不完全寄托在一艘船
上,更不是依赖某一处地方。我的全部财产,也不会因为这一年的盈
亏而受影响。
虽然《威尼斯商人》后来的剧情说明安东尼的安全措施并不妥
当。但在幕布刚刚拉开时,安东尼对自己的财产非常放心,因为他将
投资分散于不同船只、不同地点以及不同时间。
1851年,恩斯特·海因里希·韦伯(1795年6月24日—1878年1月
26日)在《触觉感官与一般敏感性》(Der Tastsinn und das
Gemeingefühl)一书中应用了伯努利的对数效用。该书成为试验心理
学的奠基之作之一。在该书中,韦伯将人能觉察出的刺激强度的最小
变化定义为“差别感觉阈限”或“最小觉差”。他认为,刺激强度的
变化除以初始刺激强度得到的是一个常数(韦伯定律)。1860年,古
斯塔夫·西奥多·费希纳(1801年4月19日—1887年11月18日)在《心理物理学纲要》(Elemente der Psychophysik)中用该定律解释:虽
然人的大脑和身体看起来是分离的,但它们其实是对同一现实做出不
同的反应。他认为,感觉量(大脑所经历的)的变化与韦伯定律中的
常数成比例。
门格尔指出,凹性效用——就是现在所说的“边际效用递
减”——并不足以解决广义形式的圣彼得堡悖论 4。例如,假设在第n
次投掷中硬币正面首次向上,赌博的奖金是e的2 n次幂。则赌博的期望
对数效用为
门格尔指出,只要效用函数是有限的,圣彼得堡类型的赌博就存
在,其期望效用是无限的。因此,许多经济学家认为,虽然效用有限
仍是个有争议的问题,但有限性是一个合理效用函数存在的前提。
门格尔还分析了解决该悖论的另一个方法,该方法后来被行为经
济学家重拾。即:个人倾向于完全忽略小概率事件产生的结果。该方
法在很早之前由数学家布丰(1707年9月7日—1788年4月16日)于1777
年在《或然算数试验》(Essaid'arithmétique morale)一文中提
出。门格尔指出,人们容易低估极端事件的概率,可能是极小概率事
件也可能是极大概率事件,从而高估中间事件的概率。
门格尔有关无界性的观察使得肯尼思·约瑟夫·阿罗(1965)提
出,不是所有的不确定性结果都满足冯·诺伊曼和摩根斯坦公理
(1947),因为只要效用函数被指定为有界的,或者有上界或者有下
界,那么完整性公理和持续性公理都将被门格尔类型的圣彼得堡悖论
打破。 [17]例如,我们可以想想这样两种赌博,第一个赌博明显优于
第二个,但两个赌博的期望效用都是无限的。不过,这些异想天开的
想法并不能难倒像保罗·安东尼·萨缪尔森这样的人。萨缪尔森
(1977)安慰道:尽管这类赌博吸引了诸多有思想的试验,“但在现
实生活中并不是很重要”。 [18]然而,在不确定经济学的发展过程
中,该悖论的确起了长期的、重大的作用,使得萨缪尔森不得不总结
说:“它在高等知识分子的脑海中拥有崇高的地位”。萨缪尔森提出了一个更令人困扰的拒绝无界效用函数的问题,即
便没有圣彼得堡悖论无限性的存在,该问题仍会出现。假设某人可以
确定得到报酬X(X为金额较大的数值)。如果他的期望效用无上界,那么总会存在一个更大的数Y,使得即便得到的概率很低他也很想得
到。无界效用即是非饱和性的一个极端形式。另一方面,在pp.209~
211中,阿罗(1974)证明:如果效用函数U(X)单调递增,成凹性,U(0)有界,而且E(X)有界,那么E[U(X)]就是有界的。 [19]因
此,如果具有无穷期望价值的圣彼得堡式赌博在现实情况中不存在,那么即便是无上界的效用函数也不会存在问题。1780年
杰里米·边沁(1748年2月15日—1832年6月6日) 出版了《道德
与立法原理导论》(An Introduction to the Principles of Morals
and Legislation)(私人印制);完整版出版于1789年。1906年
维尔弗里多·帕累托(1848年7月15日—1923年8月20日) 出版
了《政治经济学手册》(Manual of Political Economy);由意大利
文翻译成英文,Augustus M.Kelly,1971年。1951年
肯尼思·约瑟夫·阿罗(1921年8月23日—) 发表了《对古典福
利经济学基本定理的拓展》(An Extension of the Basic Theorems
of Classical Welfare Economics),载于《第二届数学统计与概率
伯克利论坛论文集》由J·内曼编辑(University of California
Press,1951年),pp.507~532;再版于《肯尼思·阿罗文集:一般均
衡》第3卷,Harvard University Press,1983年,pp.13~45。
序数效用与基数效用、帕累托最优、竞争均衡的优化
边沁(1780)宣称:人生的目标是追求幸福,而且幸福可以量
化;因此,人们在做决策时,谨慎地计算自己的幸福程度,权衡优势
与劣势。边沁写道:
自然界将人类置于两个主宰者的支配之中:痛苦和快乐。只有苦
乐能指出我们应该做什么以及决定我们去做什么。是非的标准乃至因
果的联系,都由它们定夺。
他还认为,财富是获得幸福的手段(因而从某种程度上说是衡量
幸福的指标之一),但是越来越多的财富带来的幸福增量则是逐渐减
少的——就是我们现在所说的“财富的边际效用递减”(据此他推出
赌博是“不好”的、保险是“好”的)。社会的目标是要让所有社会
成员的幸福最大化,对每个人的幸福值进行平等加权再求和就得到所
有成员的幸福值。把这些想法综合起来就要求进行把财富从富人转向
穷人这样的重新分配,虽然边沁意识到该政策的好处需要与生产率动
力降低的弊端进行权衡。财富再分配的问题之一在于如何确定哪些人
是社会“成员”(只有选民,只有男人,还是只有居民?)。尽管这
些观点后来被现代经济学家几度修改,但“效用函数之父”的称号边
沁当之无愧。
相反,希腊哲学家们则认为,每个人在社会中都扮演着各自的角
色;有些人生来就是奴隶,而另一些人——哲学家们——就应该是统
治者。男人天生就比女人优越。在他们的正义观中,某些人为其他人
谋幸福,或者某些人应该获得比别人更多的幸福,这都是天经地义
的。帕累托(1906)认识到,接受边沁提出的效用基数假设,只需简
单地将偏好解释为序数,也可以得到同样的结论。但更重要的是,他
意识到艾尔弗雷德·马歇尔(1842年7月26日—1924年7月13日)
(1890)的《经济学原理》(Principles of Economics)以及其他人
利用效用进行人与人之间的福利比较太强,因而引出了现在所称
的“帕累托最优”:一种均衡状态,在这种均衡下,不存在另外的资
源分配方式可以在不损害一部分人福利的情况下增加另一部分人的福
利(每个人都用效用评估自己的福利)。后来有人指出,竞争均衡就
是帕累托最优,自此帕累托最优就成为亚当·斯密的“看不见的
手”的强有力支持。
阿罗(1951)也证明了德布勒(1959)描述的竞争均衡的两个优
化定理:
第一优化定理:如果存在均衡,而且所有与偏好和生产相关的资
源都由市场定价,则竞争均衡定是帕累托最优;即消费者之间的资源
配置均衡发生任何变动都不可能在不损害一部分人利益的情况下改善
另一部分人的利益。
这样我们为亚当·斯密(1776)的“看不见的手”找到了现代证
据。
第二优化定理:如果生产规模不存在递增收益且其他某些小条件
得到满足,那么对于资源的初始禀赋分配而言,帕累托最优就是竞争
均衡 5。
第二个定理为判断某个配置是否为帕累托最优提供了一个有效的
方法。假定所有消费者的效用函数为凹性,那么当且仅当该配置在服
从消费总供给约束条件下已经最大化消费者效用的正加权平均之和
时,该配置才是帕累托最优。
帕累托最优是竞争价格体系的现代支持证据之一[其他的支持理
由与激励和信息沟通相关(哈耶克,1945)]:即,竞争价格体系实
现了资源在消费者和企业之间的分配,而且不存在另一种分配方式能
在不损害一部分消费者利益的情况下提高另一部分消费者的利益。第
二个支持理由是,竞争价格体系的均衡存在于“经济的核心”:资源
配置使得每个人至少不差于他的初始禀赋(每个人生来就带着一定的
初始禀赋)。当然,帕累托最优配置组合并不是独一无二的,竞争价格体系只
是挑选其中一个而已。但阿罗指出,通过重新安排消费者的禀赋(在
交换或生产发生之前)竞争价格体系可以实现任何帕累托最优配置。
因此,首先重新分配财富,然后让价格体系自由运转,社会就能实现
它所需要的帕累托最优配置。由于现代经济学家对人与人财富的比较
避而远之,因此,经济学家不会跳出来指出最初的财富分配应该是什
么,那是政治学家的事情。经济学家总是回避最让人头疼的问题。
这些定理由杰勒德·德布勒分别在1951年和1954年的两篇文章中
证明。 [20]1835年
朗伯·阿道夫·雅克·凯特勒(1796年2月22日—1874年2月17
日) 出版了《论人与其能力的发展》(Sur l'homme et le
développement de ses facultés,ou Essai de physique sociale)
(Bachelier,1835年);1942年从法文翻译为英文(Chambers,1942
年)。
普通人或典型人、正态分布、概率在社会科学中的应用
凯特勒(1835)首次提出了“普通人”概念,普通人成为社会科
学领域最著名的虚拟人物。凯特勒根据100000个法国士兵的平均身高
和体重构建了他的普通人。他还更深一步,根据这些士兵的拘捕记录
推出一个普通人的犯罪倾向。普通人的概念在金融经济学发展史上发
挥了重要作用,其影响时间长达一个世纪之久。该概念后来发展为人
们熟知的“典型人”。
凯特勒的第二个重要贡献是,他认为许多自然过程都符合正态曲
线。我的学生卢卡·巴龙告诉我,我们其实应该感谢柏拉图(公元前
427年—公元前347年)。如果我们从更深更广的角度去理解柏拉图的
作品,我们会发现是柏拉图首次描述了单峰对称频率分布,而且他相
信大多数特质都是按这种方式自然地分布的:……因为经验会告诉他事情的真实情况。善良与邪恶都是极少见
的,绝大多数人都是处于这两者之间。我的意思是……你可能想说非
常高与非常矮——非常高与非常矮的人同样是很少见的。这种特征基
本适用于所有的极端情况,不管是大与小、迅速与缓慢、正直与邪
恶,或者黑与白。也不管你是分析人、狗或者任何事物,你都能发现
极端的情况总是极少数,更多的情况是位于中间。见《西方世界的伟
大著作,第1卷:柏拉图篇》(Great Books of the Western World:
Plato , Volume I : Phaedo ) , Franklin Library , 1979 年 ,pp.385~439,尤其是p.415。
凯特勒为正态分布增添了更为具体的特征 6,观察到他的结果有个
重要前提,那就是除了在被考察的差异唯一来源上,样本在其他各个
方面都必须足够同质化。凯特勒对他的正态法则非常自信。因此,当
他观察到身高最低的那个士兵组的人数竟然多于身高较高组的人数时,他就指出,由于服兵役是自愿的,身高最低组的士兵人数较多就
证明了大约有2000人欺骗性地回避了征兵。
1843年,安东尼·奥古斯丁·古诺(1801年8月18日—1877年3月
31日)表达了对将概率论应用于社会科学的严重担忧。 [21]令所有人
都很惊讶的是,在1838年古诺就将数学分析方法引入经济学。他的观
点与他1838年的书一样,都远远领先于那个时代。可是问题出在选择
可验证假说上。古诺认为,社会科学提供了大量挑选与划分数据的方
法,结果造成某些样本看起来支持假说,而且碰巧验证结果在统计上
非常显著。但其实这一结果并不可信。他写道:
很显然,随着我们将样本划分得越来越细,就概率而言,我们就
越有可能得到至少一个小样本其男女出生比率明显不同。
古诺还特别担心人们极易在挑选数据之后再选择假说。现在对这
类错误我们有个名词叫“数据挖掘”。
亨利·托马斯·巴克尔的观点则是另一个极端。他表示:期待有
一天,统计学的力量能融入社会科学,通过数学的运用让社会科学也
能得出像物理学一样精确的预测度。 [22]显然,日后的发展证明,实
际情况介于古诺与巴克尔的观点之间。不过在20世纪中叶,最著名的
科幻小说家艾萨克·阿西莫夫(1920年1月2日—1992年4月6日)在其
小说《基地三部曲》(The Foundation Trilogy)(1951~1953)预
测,大规模应用的社会统计方法将对几百年后的主要社会趋势做出预
测。1900年
路易斯·巴舍利耶(1870年3月11日—1946年4月26日) 发表了
《投机理论》(Théorie de la spéculation)一文,载于《巴黎高等
师范学院科学年鉴》,第17卷,pp.21~86;后由A.詹姆斯·博尼思在
保罗H.库特纳编辑的《股票市场价格的随机游走特征》(The Random
Character of Stock Market Prices)(Risk Publications,2000
年,pp.18~91)一书中翻译成英文;还以法文再版于《投机理论与数
理 游 戏 理 论 》 ( Théorie de la speculation théorie
mathématique de jeu),1995年,pp.21~86。
布朗运动、期权定价、随机游走、正态分布
巴舍利耶(1900)在博士论文中写到,概率论可以用来描述证券
价格的波动。他极可能是有记载以来,进行此类尝试的第一人。巴舍
利耶首次对一个时间连续、状态连续的过程(算术布朗运动)进行了
数学描述,其目的竟是为了对“期权”定价(法语为年金,或者永久
政府债券)。虽然他只部分实现了他的目标,但他的论文——递交给
巴黎科学院的论文——却比爱因斯坦对布朗运动的分析领先了6年,比
布莱克-斯科尔斯公式(基于几何布朗运动)领先了73年之久。
他极有远见地提出现在大家熟知的随机游走与正态分布假设。他
证明了随机性并指出:以当前的价格来看,相信价格上涨的买家人数
与相信价格下跌的卖家人数肯定是一样的。既然我们没有理由判断哪
组人更明智,因此价格接下来向上变化或向下变化的概率是一样的。
于是,他总结到,证券买卖者的期望利润应该是零,证券市场是
个“公平游戏”。
价格随机游走让巴舍利耶发现了我们现在公认的一个结果,那就
是波动幅度与时间区间的平方根成正比 7,而且他还推出了一个描述资
产价格扩散的差分方程。他观察到,如果价格变化是序列独立的而且
在较短时间区间内方差是有限的同分布随机变量,那么根据拉普拉斯
(1749年3月23日—1827年3月5日)(1814)的中心极限定理,较长时
间区间内的价格变动就近似为正态分布。 [23]巴舍利耶还推出了第一
个公开发表的期权定价公式,而且对此进行了经验验证,结果发现市
场价格与他计算的理论价格非常相似。他在论文结尾这样写道:可能最后的备注并不是没有意义的。如果说,在本文讨论的几个
问题方面,我比较了实际观察结果与理论预期结果,这并不能说明结
果证明了根据数学方式建立起来的公式,而只能说明市场不自觉地遵
循着一定的定律,这就是概率定律。
这位金融经济学领域的文森特·凡·高,最终博士论文只得了个
平均分。有意思的是,我们现在将其视为金融经济学领域最杰出的论
文。1906年,巴舍利耶出版了《连续概率理论》(Théorie des
probabilitiés continues)(Gauthier-Villars)。在书中,他定义
了几种随机过程类型,包括随后重新发现的马尔可夫与奥恩斯坦-乌伦
贝克过程。他从漂移与扩散系数角度描述随机过程。尽管巴舍利耶成
绩卓著,可是直到书出版几年后他才找到一份教职。而且从那时开始
一直到1937年他退休,也就是1946年他去世之前9年,他都屈身在一个
毫不起眼的岗位。在很不幸地被人遗忘50多年之后,巴舍利耶的论文
重新被萨缪尔森发现。萨缪尔森在2000年2月8日美国PBS电视节目“新
星2074:30亿赌注”中说道:
在20世纪50年代早期,一个偶然的机会我从巴黎大学图书馆找到
这本不知名的、已经破烂不堪的书。当我翻开它时,感觉就像一个全
新的世界在我面前展开。事实上,我边读就边想一定要将该书翻译成
英文,让大家都来欣赏这熠熠生辉的学术珍珠。 81921年
弗兰克·海尼曼·奈特(1885年11月7日—1972年4月15日) 出
版 了 《 风 险 、 不 确 定 性 与 利 润 》 ( Risk , Uncertainty and
Profit),(Houghton Mifflin),1921年。
风险与不确定性、企业利润来源、投资分散化
奈特(1921)因为两个观点而出名。第一个是他对“风
险”与“不确定性”的区分;第二个是他找到了企业在不确定性条件
下获得经营“利润”的来源。奈特的分析有些让人困扰,很容易让人
用现代的方式误解他的作品。奈特将风险理解为概率可以或多或少进
行客观计量的情况,或者是大数定律能发挥作用通过组合几种可能的
结果进而消除不确定性的情况。
正如我们已经反复重申的,任何一种不确定性,只要它能通过某
种方法简化为一个客观的、可以定量化的概率,那么它就能通过个案
分组简化为完全确定性。(第7章)
而另一方面,奈特将不确定性理解为单一异常事件或者是科学无
法进行清晰预测的事件。一个典型的例子就是在人类事务中人们无法
清晰判断其他人的决策制定能力与决策结果。奈特认为,对于不确定
性事件,我们谈概率是毫无意义的——该观点后来对人们,特别是对
埃尔斯伯格(1961)挑战基于主观形成概率信念的预期效用最大化的
有用性发挥了重大作用。
早在1755年,理查德·坎蒂隆(大约1690年~1734年5月14日)出
版的《商业性质》(Essay of the Nature of Commerce)(实际上写
于18世纪20年代)一书就已经认识到,企业利润来源于企业支付所有
费用(包括利息、工资以及租金)之后企业剩余的报酬。然而,在确
定条件下的竞争性经济体中,所有利润都被竞争化,均衡状态下的利
润为零。于是奈特提出,只有在未来是确定不可知的经济体中,利润
才会增加。如果能获得奈特的许可,我想将他的理论用如下数学公式
(奈特并没有用该公式)加以表达:
r j=r+δ j+ε j (1-14)其中,r j表示企业j的股东已实现的收益,r表示无风险收益,ε j表
示企业已实现收益中能被分散化消耗的部分。现在,我们将ε j称
为“剩余风险”带来的收益。剩下的δ j是奈特将其与不确定性联系起
来的收益部分,也就是奈特所称的“利润”指标。奈特将利润理解为
企业收益中无法被分散化、被套利以及被承保的随机部分。是什么带
来了这部分收益呢?奈特指出,如果概率分布不能被客观地计量,那
么不确定性就不能被分散化。而且最重要的是,人们的决策结果,如
制定企业方针、在企业内选择授权对象,都无法通过概率进行量化预
测。于是,“企业家精神”成为企业利润的最终来源。
能带来利润的唯一“风险”是一种独特的不确定性,他来自一种
终级责任感的实施。该责任感本身无法承保、无法资本化亦无法薪酬
化。利润源自事情固有的、绝对的不可预测性,源自一个坚定的事
实,那就是人类活动的结果无法被预期,就它们进行概率计算是根本
不可能的,也是毫无意义的。(第10章)
δ j的期望价值是多少呢?对奈特而言,由于我们现在所说的如下
行为因素的原因,市场最好预测E(δ j)<0。第一,企业家可能过度
自信进而过度投资;第二,因为不能理解所谓的“赢家诅咒”而过度
支付;第三,一旦已经投入资本就不愿意放弃计划;第四,为自己工
作的满足感。不过,奈特的脑中显然没有我们现在称为“系统风
险”的概念。系统风险是指整个社会都面临的风险,每一个个体都无
法逃脱,无法不因此牺牲期望收益的风险。1923年
约翰·梅纳德·凯恩斯(1883年6月5日—1946年4月21日) 发表
了 《 论 商 品 市 场 的 某 些 问 题 》 ( Some Aspects of Commodity
Markets),载于《曼彻斯特卫报》,1923年。1949年
霍尔布鲁克·沃金(1895年—1985年10月5日) 发表了《存储价
格理论》(The Theory of Price of Storage),载于《美国经济评
论》第39卷,第6期(1949年12月),pp.1254~1262。
即期价格与远期价格、远期价格与期望价格、正常逆价、便利收
益、套利与投机
金融经济学吸引经济学家最早的问题之一便是期货交割的今日价
格(期货价格或远期价格F 0)与未来标的资产在交割日的期望价格
E(S t)的正常关系。凯恩斯(1923)在一篇刊登在报纸上的文章中首
次提出了期货市场的“正常逆价”(normal backwardation)理论
(也称现货溢价或期货折价理论)。他指出,F 0通常低于S t的预期价
值。他认为,通常做空的套利者为了让投资者接受风险不得不向他们
支付一定风险溢价。凯恩斯(1930)更详细地阐述了这个观点。 [24]
当然,我们不难理解,对于某些类型的标的资产,套利逻辑(对
此我会进行更新并加入风险规避)会产生正常逆价现象。例如,如果
标的资产是某股票市场指数,假定没有套利且市场完备,则F 0=S
0(rd) t,其中S 0为标的资产的当期价格,r为无风险收益率,d是
指数的回报率,t是交割期。通常,由于风险规避意味着E(S t)>S
0(rd) t,因而我们得到F 0
用于消费或生产目的的标的资产(也就是商品)非常有意思。对
这些资产,由于标的商品不能轻易卖空(借用或者出售),套利无法
使得F 0=S 0(rc) t,其中,c等于1加上存储成本率;它只能保证S
0c t≤F 0≤S 0(rc) t。对于E(S t)
样的情况。因此,在考虑持有标的商品的机会成本之后,商品的远期
价格是否会低于其预期即期价格就是个非常有趣的问题。用公式表达
为:F 0< E(S t)(rc) t。这为商品的当期所有者带来的额外收
益,该收益被尼古拉斯·卡尔多(1939)称为“便利收益”。 [25]
正如约翰R.希克斯(1904年4月8日—1989年5月20日)(1939)所
言,投资者通常不得不被劝诱购买商品期货,因为他们本来不喜欢这种状态。 [26]
他们知道,已经提前安排好的某一特定日期的需求与供给(通过
远期合约)与那天真正到来时的供需没有什么关系;尤其是,他们根
本无法提前准确说出在未来时期他们自己到底愿意买多少或者卖多
少。因此,一个正常生意人愿意签订远期合约的原因只能是这样做他
能“套利”——也就是说远期交易能降低他现在面临的风险。而且只
有在他以某种方式承诺进行销售或购买行为时这种情况才会发生……
技术环境使得企业家控制投入要素的获取比控制产出的完成更加自
如。投入要素大多是用于开始新的流程;而产出的生产流程……可能
已经开始。因此,虽然有些人期望能固定一个未来买入计划,但更多
时候人们更希望固定一个未来出售计划。(第2版,p.137)
凯恩斯和希克斯认为,在选择什么时候、是否购买以及向谁购买
生产投入要素方面时,商人通常具有较多弹性(现在我们称他们拥有
更有价值的“实物期权”)。而当商人不得不销售由他们部分或者完
全负责的产出时,则弹性较小。按照凯恩斯和希克斯的说法,商品的
需求方存在“先天劣势”。弥补远期交易需求疲软的是投机者,他们
缺乏做多的自然理由。为了让投机者做多而且承担风险,必须付给投
机者一定的便利收益(即更低的远期价格)。
由于无法观测到预期的未来即期价格,正常逆价的特征就是随着
交割日的临近,远期价格逐渐上升(高于持有商品的机会成本)。
通常人们认为,期货的今日价格大部分取决于人们今日对期货在
未来交割日的即期价格的预期。而且,由于交割日不同带来的相同期
货的价格差异反映了人们对不同日期即期价格的预期差异。沃金
(1949年12月)指出,这并不总是正确的。
沃金指出,即便商品的即期价格发生变化,或者预期收成发生变
化,时间t(比如2006年1月)市场报出的将于时间t+k(比如2006年9
月)交割的商品的期货价格与时间t+h(比如2006年3月)相同商品的
价格之比是稳定的。沃金提出,这个观点成立的一个重要条件是商品
的当期库存相对于预期未来库存较为充沛,因此我们可以存储商品至
远期交易。因而,商品的当期价格可以进行调整使得商品持有人只要
能弥补他将商品留作存货的存储成本,那么他不管是在时间t、t+h,还是t+k售出商品都是无差异的。由于商品存储时间越长,存储成本就越高,因而在更远期交割的期货价格比在近期交割的期货价格要高,差异产生的原因就在于存储成本。
但有的时候期货价格会发生倒转,导致近期期货价格高于远期期
货价格。一旦相对于未来需求而言当期库存较低或者未来收成预期较
大时,这种情况就会发生。这时,我们不应该将任何当期存货持有到
远期,所有存货都应该在下次收成之前全部消耗掉。这使得期货价格
不再受存储成本的影响,并带来“便利收益”。1930年
欧文·费雪(1867年2月27日—1947年4月29日) 出版了《利息
理论》(The Theory of Interest:As Determined by Impacting to
Spend Impatience and Opportunity to Invest It),Macmillan,1930年。
跨期消费、生产、汇率、利率、费雪效应、急躁与机会、费雪分
离定理、竞争性市场、一致同意与帕累托最优、实物期权、投机、资
本预算
费雪(1930)是20世纪大多数投资金融理论的奠基之作。费雪完
善并重述了早前出现在费雪(1896)、费雪(1906)和费雪(1907)
中的许多研究成果。 [27]费雪指出,他的部分思想受到约翰·雷
(1796年6月1日—1872年7月12日)1834年论文的启发, [28]为此,费
雪还将其1930年的著作献给雷。费雪创建了第一个正式的、描述既有
跨期交易又有生产的经济系统的均衡模型。在这个过程中,他一下子
就推出计算财富的自然经济结果就是计算现值,他还证实生产的目的
是为了使现值最大化。另外,他还分析出了用于计算现值的利率的影
响因素。
费雪假定,每一个市场参与者都同时是某一大类消费商品的消费
者与生产者。单一商品的简化使他能从多商品瓦尔拉斯范式下不必要
的纷繁复杂中进行抽象提炼。而且自那以后单一商品的假定成为金融
理论研究的核心。每个交易日,交易受到一笔期末到期、无违约风险
的短期债券的收入的影响。在该分析框架下,费雪对经济思想史的贡
献在于:①分析了实际利率的影响因素以及总消费的均衡跨期路径;
②提出“费雪效应”,分析了名义利率与实际利率以及通货膨胀率之
间的关系;③提出费雪分离定理,指出应该将生产决策授权给以现值
最大化为目标的企业,而不需要直接依赖股东偏好;企业的融资与生
产决策应该分离开来。投资金融理论的大多数后续工作都可以看成是
对费雪观点的进一步完善,尤其是在分析中加入了对不确定性的考虑
以及使用更为复杂的金融工具用以分析消费跨时间与跨地区的分配。
费雪将现有两种解释利率的观点协调起来。一种观点从产出效率
(“机会”)出发,另一种则是基于消费心理学或时间偏好——或
称“急躁”。“急躁”一词是由费雪(1907)在《论利率》一书中创造出来的,用以提出一个综合性理论:“因而,利率的存在是因为人
们总想尽早消费,一刻也不耽误;而如果让你推迟消费,那么你的未
来收入就要增加,这增加的部分就是利率”(p.495)。
费雪通过文字、图表以及公式三种方式来描述他的经济系统。有
意思的是,即便经济思想史发展到此时,费雪发现使用代数公式仍是
非常有用的。他指出,使用公式可以让人很清楚地知道,待求变量的
个数与独立方程的个数是一样的。另外,他还写道:
认为用数学公式描述经济问题只是展示了一个不符合实际情况的
理论精确模型的观点是完全正确的。但是,在我看来,这绝对不是一
个缺点,而恰好是个优点。因为我们可以根据数学公式清楚地指出哪
些地方是不符合实际情况的。(p.315) 9
费雪设计了一个只有2个时间段3个消费者的简单例子。在这个例
子中,只有消费者的时间偏好影响利率。设:
r为均衡无风险收益率;
为第i个消费者在时间0和时间1的初始消费金额;
x i
0,x i
1为第i个消费者在时间0和时间1选择的借款或放贷金
额,消费者的预算约束为 x i
0+x i
1r=0;
[29]是第i个消费者
在时间0和时间1选择的最优消费金额。
接着,他假设消费者的时间偏好率取决于他选择的消费流:f i=F
i(C i
0,C i
1)是消费者i的时间偏好率。
在第12章的附录中,费雪将时间偏好率与消费效用U i(C i
0,C
i
1)联系起来:f i=[U′ i(C i
0)U′ i(C i
1)]-1 (1-15)
他提出,在均衡状态下,每个消费者的时间偏好率都必须等于无
风险收益率,即:
f 1=f 2=f 3=r (1-16)
为了让市场出清,他要求在每个时间所有消费者的净借款与贷款
额为零:x 1
0+x 2
0+x 3
0=0,x 1
1+x 2
1+x 3
1=0。这样,一共有7个未知
数:C 1
0、C 2
0、C 3
0、C 1
1、C 2
1、C 3
1以及r,相应有7个独立方程。
费雪的经济系统
设:
U(C 0),U(C 1)为时间0和1的消费效用;
ρ为急躁率;
Ω 0为消费品的初始禀赋;
X 0为Ω 0已经用于生产的部分,这样C 0=Ω 0-X 0;
f(X 0)为时间1消费品被用于生产而得到的产出,这样C 1=f(X
0);
W 0为消费者的现有财富,因而W 0=C 0+C 1r。
假设U′(C)>0(非饱和),U′′(C)<0(边际效用递减),0<ρ<1(更偏好当期消费而不是未来消费),f′(X 0)>0(投入增加
产出增加),以及f′′(X 0)<0(规模收益递减)。
消费者的生产问题为,约束于C 0=Ω 0-X 0以及
C 1=f(X 0)
代入约束条件,对效用函数求微分,并让导数等于零以得到最大
值,则得到:
消费者的交易问题为:
,约束于W 0=C 0+ C 1r
同样,代入约束条件,对效用函数求微分,并让导数等于零,便
得到:
把上面两个结果联系在一起,就得到:
这样,我们就得到利率的双边决定因素:均衡无风险利率等于我
们现在说的边际替代率(费雪称为“时间偏好率”),也等于资本的
边际产出效率。再举个更具体的例子,设U(C t)=lnC t,f(X 0)=αX β0,其
中0<β<1且α>0。这满足效用函数与生产函数的求导条件。α可以解
释为产出效率的纯指标,因为α越大,一定投入带来的产出就越多。
代入方程(1):
解未知数C 0和r,得到:
C 0= ( 1+ρβ ) -1Ω 0 , 且
对无风险收益率公式求导:
于是我们看到了费雪提出的急躁率(ρ)与机会(α)对利率的
完全独立影响。
费雪还指出,不同时间段的独立利率是经济力量的自然结果,在
完备市场中是无法通过套利消除的。
另一个推论就是,我们有必要为每个不同的时间段设定一个独立
的利息率。用更务实的话来说,我们需要认识到短期利率与长期利率
的差异。该差异不像博姆-巴韦克想的那样是因为市场不完备引起的因而可以消除。这些差异之所以产生是因为企业收入流的构成存在无穷
尽的变化。任何单纯的价格套利都无法消除这些差异。(p.313) 10
费雪总结到:利率受到以下因素的影响:①不同时间资源禀赋的
相对分布;②消费者与投资者的时间偏好;③将当期总禀赋转化为未
来总消费的生产机会;④资源禀赋的一般规模;⑤风险规避与风险的
时间结构;⑥预期的通货膨胀率。费雪将因素②产生的原因归结为缺
乏远见、无法自我控制、习惯形成、预期寿命以及遗赠动因,这显然
是一种行为导向的解释。他说明了所有这6个因素如何影响经济参与者
的决策以及这些决策又是如何最终影响均衡利率的。
接着,费雪分析了他的理论可能受到的批判。其中一个大家常质
疑的就是将利率的影响因素与跨期消费选择的特征联系在一起可能是
个不错的想法,但这样做太狭隘。事实上,利率主要是由“可贷资金
的供需关系”决定的。费雪回复到,资金的供需只是更为基本的生产
者现值最大化的需求以及消费者最优化平衡人生各期消费的需求的中
间效应。不过,他也承认,可能还有些他尚未涉及的复杂的制度因素
会影响利率,但那些因素的影响是次要的。
费雪将他的分离结果表述如下:
但我们看见,在我们所假设的一个充满选择的世界中,资本家通
过结合两类收入选择实现了其最终收益。在我们的假设中,这两种收
入选择是完全独立的。再重述一次,这两类选择是:第一,从各种可
能的收入流中选择具有最高现值的收入流;第二,通过借贷或者买卖
选择该收入流各种可能的修正方式。第一个选择是在具有不同市场价
值的收入流之间进行选择;第二个是在具有相同市场价值的收入流之
间进行选择。(p.141) 11
必须谨慎解释这种“分离”,它并不意味着第二个选择完全独立
于第一个选择。要弄清楚第二个选择到底是什么,我们首先得知道第
一个选择的含义。不过,可以在做出第二个选择之前做出第一个选
择。费雪还清晰地指出,他的分离结果取决于一个竞争性市场,在这
个市场中,资本家自身并没有意识到他们可能对利率造成影响。另
外,费雪指出,他的结果需要假定借款利率和贷款利率是一致的(市
场完备)。这表明,企业的行为是追求现值最大化。在不知道股东的偏好和
禀赋的情况下,企业制定的生产决策与它们的股东是一致的。如果的
确如此,那么这可以大大简化竞争经济中的资源配置问题。
对费雪分离定理的证明
为了推导分离定理,继续我们之前的例子。假定将生产决策委派
给一个追求现值最大化的企业。这样的企业将选择X 0来使:
其中不考虑可能多r产生的影响(即选择X 0时,dX 0dr=0)。对
现值进行微分并将之等于0。那么r=f′(X 0),这与代表性的消费者
自己制定决策的结果完全一样。
尽管如此,马克·鲁宾斯坦1978年提出,费雪分离定理(在完备
与竞争性的金融市场中,以现值最大化为目标的企业所做出的投资决
策是全体股东都一致同意的)基本上是错误的,在一个投资者充分分
散化的市场尤其如此,这是因为竞争假说并不稳健。 [30]
有时,完全竞争被定义为要求任何一家企业的行为都无法影响价
格。1934年,琼·维奥莉特·罗宾逊(1903年10月31日—1983年8月5
日)针对边际生产成本递增的商品对该要求的实际合理性提出了质疑
(如果在所有企业都以相同价格销售相同商品的市场中,不止一个企
业生存下来,那么边际生产成本就是递增的)。因为此时,企业数目
必须是无穷多的。在企业数目有限的情况下,一家企业增加产出,其
他企业的最优产出就相应降低。其他企业产出的降低会部分但不会完
全抵消那一企业产出的增加,从而使得商品价格发生一定程度的变
化。 [31]她总结道:
如果我们都承认如下情况为完全竞争:一家企业增加一单位产出
所造成的价格下降幅度小于某个特定的有限数额。那么,不管边际成
本曲线的斜率如何,都存在一定数量的企业使得市场实现完全竞争。
边际成本曲线的斜率越小,企业数目就越少;边际成本曲线的斜率越
大,企业数目就越多。(p.119) 12如果根据罗宾逊的经典论文来定义竞争,那么全体股东一致同意
的情况就基本上不会发生(凭经验,发生的概率极低)。我们只需要
用一个确定状态下的单一时期经济体就可以说明。其基本思想在于当
市场上存在大量小企业,每一个企业的生产决策对利率的影响都微乎
其微(效应1),同时充分分散化的投资者也只将自身财富的一小部分
投入单家企业。因此,单家企业对投资者财富的影响也是微乎其微的
(效应2)。这样,在为企业生产决策投票时,每个投资者都需要在这
两个效应之间进行权衡。由于一部分投资者(贷方)希望利率较高而
另一部分投资者(借方)希望利率较低,他们会意见不一。罗宾逊在
论文中指出,增加企业数目并不能解决这一问题,其结果只能是导致
两种效应都同比例降低。
虽然基于现值计算做出的决策通常并不能得到所有投资者的一致
同意(除非他们是完全相同的),但仍是帕累托最优。他在论文中指
出,现值最大化的最大好处在于,不管企业股东是谁,企业都能根据
该方法做出帕累托最优投资决策,而且是唯一的方法。尽管该论文在
20多年前已经出版,基础性金融学教材仍然一致同意在这个错误假设
基础上推出现值最大化的合理性。其中一本著名的教材仍将“一致同
意”列为金融经济学的七个伟大思想之一。
费雪可能是首位强调我们现在所说的“实物期权”对提高柔性生
产机会作用的经济学家。柔性生产机会对如今企业投资的现值计算起
着重要的作用。
这为我们带来了大量重要的选择类别;即我们可以选择更新或修
理设备,还可以选择进行不同程度的更新与修理……但是,除了选择
保留稳定数量的商品库存外,企业主还有许多其他选择。他可以选择
以赚取利润的速度扩大企业规模……第三个选择是逐渐关闭生意……
另一类收入流选择常见于对不同生产方式的选择,尤其是对不同程度
的所有资本主义生产方式的选择……企业家们面临的这些备选方案通
常可以划分为短期决策和长期决策。短期决策涉及一些构造简单、易
消耗的设备;而长期决策涉及生产成本巨大、但极为耐用的设备。……在上述所有情况中,只要企业选择能使未来收入流现值最大化的
设备更新、修理或者改良决策,企业就能得到“最优”结果。
(pp.194~199) 13
费雪还分析了利率变动的动态特征。例如,利率的变化可能改变
人们对生产机会的利用,而这又反过来稳定了利率,造成我们现在看到的均值回归现象。
尽管费雪对不确定性的一阶效应进行了定量分析,但他同时也表
示,要对理论进行正式归纳不容乐观:
试图用数学公式有效且全面地描述随机波动的利率的决定机制,就如同试图准确描绘在风力作用下导弹的轨迹一样。这样的数学公式
要么得具有高度的总括性,要么完全是经验式的,否则都会失去价
值。(p.316) 14
于是,费雪把大量经济现象都留给他人来解释,如同时使用保
险、债务和权益,对流动性的需求,投资组合分散化,具有不同收益
证券类型的高度多样化,所有这些现象的存在都依赖于不确定性。
费雪在1906年出版的《资本与收入的性质》中阐述了他对市场理
性以及投机作用的观点。
当人们投资公开发行的证券时,通常会出现一种现象,即人们往
往不是独立地对证券价格进行预测。此时,投机的结果就会尤为不
幸。出现危机、恐慌、银行挤兑等事件的主要原因就是人们不是独立
进行风险估计,而是相互模仿。……而另一方面,只有当投机是基于
独立知识时,投机的效用才是最大的。投机者的专业知识可以降低风
险,而且还可以让风险从缺乏知识的人身上转移到拥有知识的人身
上。……风险是最可怕的经济罪恶之一,所有有助于消除风险的方法
——不管是保证、安全保护、远见、保险或是合法投机——都能为人
类造福。(pp.296~300)
1958年,杰克·赫希雷佛将企业的资本预算理论整合进费雪的同
期消费与投资选择模型。他设定了一个较强的经济基础,解决了许多
有关现值使用以及将内部收益率作为投资标准的争端。而且,他还分
析了一些市场不完备现象如借贷利率差异的影响,分析了资本预算以
及相互排斥投资项目的选择。 [32]1931年
哈罗德·霍特林(1895年9月29日—1973年12月26日) 发表了
《 可 耗 竭 资 源 经 济 学 》 ( The Economics of Exhaustible
Resources),载于《政治经济学》第39卷,第2期(1931年4月),pp.137~175。
可耗竭资源、霍特林法则、视为期权的矿产开采、黄金
假定(按照我们现在的说法)没有套利、市场完备且充分竞争、没有不确定性,霍特林(1931)得到这样一个结论:可耗竭资源(如
稀有金属、铜、石油等)的价格必然以无风险利率的速度增长。这通
常被称为“霍特林法则”。我们假定P 0为每单位资源今天的价格,每
年的无风险利率为r,那么在t>0年之后,每单位资源的价格将变为P
t=P 0r t。他的理由如下,在竞争均衡状态下,资源的开采速度应该保
持在这样一个水平:在两个时期之间转移开采不再带来任何边际收
益。这样,不管资源拥有者决定在今天还是在今后某天(t>0)开采并
销售资源,他拥有资源的现值都是一样的。但是如果这是真的话,那
么未贴现的价格就必须以无风险利率的速度增长,即如果P 0=PV 0(P
t),则P t=P 0r t。由于存在开采成本,该法则的含义应该修改为扣
除开采成本之后的价格应该以r-1的速度增长。接着,霍特林指出,人
们对可耗竭资源会迅速耗竭的普遍担忧是没有必要的。只要资源行业
是竞争性的,资源就会以社会最优的速度进行开采,而且无需政府干
预。
霍特林自己没有将法则推广到不确定的情况,而是将工作留给了
他人。在这里,我们有必要区分两种不确定性:①供给不确定,原因
可能来自开采成本、矿容量或者勘探速度;②需求不确定(即使用资
源的未来价值)。金融经济学家对后者尤其感兴趣。比如,假设有一
口油井,我们知道它的容量和开采成本,那么它的开采速度应该是多
少?奥克塔维奥A.图里奥(1979)首次把这个问题当做期权来进行分
析。 [33]他比较了两种选择,一是选择开采资源,一是选择执行一个
永久保护性的美式看涨期权,标的是成交价已知且固定的石油价格
(比如开采成本)。正如一个人绝不会优先提前执行这样一个看涨期
权一样(萨缪尔森-默顿,1969),这个人应该同样不会开采石油。然
而,与之相矛盾的是,现实生活中人们仍然在开发石油。图里奥的回答是,因为开采成本以足够快的速度增长,使得开采达到最优水平。
然而,如果开采成本是固定的,图里奥就仍没解开这个谜团。很显
然,即便开采成本已知而且是固定的,经济系统也不会选择永不消费
石油。虽然之后的分析大部分解决了有关用于消费的可耗竭资源的这
个谜团,但对于像黄金这样主要用于投资而不是消费目的的资源,这
个问题仍悬而未决。即便我们不用担心私人金矿会被国家征收,这个
问题还是存在的。
1990年,迈克·约翰·布伦南在美国金融学会主席致辞中分析了
如下问题:如果黄金主要是用于投资目的,开采成本的增长速度又慢
于利率,而且金矿不会被国家征收,那么金矿所有者为什么要开采黄
金呢?这个开采黄金的机会就类似于一个永久性美式开涨期权,人们
不会提前执行。然而,布伦南观察到,企业仍然在开采。他认为,这
是因为如果要让公司股票有个合理估值,企业需要开采黄金向投资者
证明他们确实拥有他们宣称的黄金储备量。 [34]然而,布伦南的解释
给我的感觉则是难以令人信服。不过,就像夏洛克·福尔摩斯所说
的,一旦我们分析并拒绝了可能的解释,不管剩下的是多么不可能,都肯定是真的。1933年
阿尔弗雷德·考尔斯三世(1891年9月15日—1984年12月28日)
发表了《股票市场预测师真具有预测能力吗?》(Can Stock Market
Forecasters Forecast?),载于《计量经济学》第1卷,第3期
(1933年7月),pp.309~324。
投资业绩、有效市场
考尔斯(1933)可能是第一本公开出版的对专家“战胜市场”能
力进行统计检验的著作。考尔斯分析了1928~1932年期间16家金融机构
对个股的7500个推荐意见。他对样本进行了如下特征描述:
预测者包括各个代表性领域的知名机构,它们大部分都规模庞
大、资金充裕,聘用能力非凡的经济学家和统计学家。……一些预测
者看起来似乎得到了德尔斐神谕的指示,用一些模棱两可的语言来表
达他们的预测。(p.309) 15
依据推荐意见得到的年投资收益比市场平均收益低1.4%。考尔斯
比较了实际预测者的收益分布与由随机挑选股票组成的投资组合收益
的分布,他发现,还是没有显著的统计证据表明预测者的能力强过市
场。他还考察了20家顶级火险公司的投资与24份金融出版物的预测,仍没有找到能够战胜市场的证据。而且,那些最失败的投资者似乎比
随机投资的业绩还要差。
1968年,J.G.克拉格和伯顿G.马尔基尔提供了一份与考尔斯类似
的最新研究。他们着重考察了证券分析师预测公司未来盈利的准确
度。令他们惊讶的是,他们发现分析师的预测并不比我们根据过去的
盈利增长进行简单推算来得更准确。 [35]1934年
本杰明·格雷厄姆(1894年5月8日—1976年9月21日)和戴维L.多
德 出版了《证券分析:原理与技术》(Security Analysis:
Principles and Technique)(McGraw-Hill,1934年);多次修改
后,作者包括杰明·格雷厄姆、戴维L.多德和西德尼·考特勒
(McGraw-Hill,第4版,1962年)。1949年
本杰明·格雷厄姆出版了《聪明的投资者》(The Intelligent
Investor),第4版(HarperCollins,1973年),首次出版于1949
年。
证券分析、基本面分析、资本结构、增长与价值、再平衡、定投
法、有效市场、数理金融、投资业绩的极端值
在最为著名的有关股票市场的著作中,格雷厄姆和多德(1934)
宣称,考察投资价值以及设计投资技巧的最基本方法是分析资产负债
表和损益表。从随后的研究发展来看,他们的主要不足在于:①没有
充分考虑投资分散化的作用;②没有考虑风险在均衡状态下对价值决
定的影响;③没有充分考虑促使市场信息有效的因素。
格雷厄姆和多德对企业资本结构相关性问题的探讨很有启发性。
他们比较了3家企业,它们每年的经营现金流相同(都是1000000美
元),但资本结构不同,可参见表1-5。
表 1-5 (单位:美元)
假设债券的利率为5%,股票价值与股票收益比率为10∶1。这样,对企业B,股票收益=1000000-(0.05×5000000)=750000;对企业
C,股票收益=1000000-(0.05×10000000)=500000。依据10∶1的资
本化率,企业B的股票价值=750000×10=7500000;企业C的股票价值
为=500000×10=5000000(pp.461~463,原始版,1934)。他们立即发现,这个情况是他们始料未及的,因为具有相同现金
流的3家企业居然总价值不同。这个表格告诉我们,企业一旦改变资本
结构,企业价值就会受到影响。这引发他们提出一个问题:“资本结
构的随意变动是否能改变企业价值?”在更详细考察之后,格雷厄姆
和多德指出,企业A的股票其实可以解释为企业B的债券与股票的组
合 。 因 此 , 理 论 上 , 企 业 A 的 股 票 价 值 应 该 为 =
5000000+10×(1000000-0.05×5000000)=12500000。这与莫迪格利
安尼-米勒(1958)和莫迪格利安尼-米勒(1969)的分析已经极为接
近。此时格雷厄姆和多德距离投资史上最为重要的思想之一仅有一步
之遥。遗憾的是,他们紧接下来的分析却偏离了前途光明的大道:
但是在现实生活中,企业A的12500000的股票价值通常无法被实
现。显而易见的理由是,普通股的购买者不会意识到普通股发行中存
在“债券组成部分”;而且在任何情况下,投资者都不希望出现这个
债券构成,因而不愿意为此进行额外支付。这个事实告诉了证券购买
者以及企业管理层一个重要原则,那就是:
企业最适宜的资本结构中,高级证券的组成部分应该是可以安全
发行并用于投资购买的证券。(p.463)
格雷厄姆(1949)在其投资经典之作《聪明的投资者》中有力地
阐述了他的投资哲学。被称为“价值投资之父”的格雷厄姆建议人
们:应该在仔细分析企业基本面的基础上进行投资,要密切关注市盈
率(PE)、股息率以及证券分析中使用的其他工具,只投资于那些股
票市场价值尚未偏高于企业有形资产价值的股票。虽然有些成长型股
票事后显示收益率很高,但格雷厄姆认为,这些股票的价格可能发生
不可预测的极端波动,投资的风险太大,不值得推荐。他的基本原则
是将可投资财富在高等级债券与由10~30只股票组成的投资组合之间进
行划分,保持两类投资占总财富的比例至少为25%。然后定期进行调整
实现预定的目标比例。他还推荐定投法,即投资者定期投入相同金额
购买普通股,而不是一次性投入。他认为“按照这种方法,当市场下 ......
投资思想史(珍藏版)
A History of the Theory of Investments:My
Annotated Bibliography
(美)马克·鲁宾斯坦(Mark Rubinstein) 著
张俊生 曾亚敏 译
ISBN:978-7-111-38839-5
本书纸版由机械工业出版社于2012年出版,电子版由华章分社(北京
华章图文信息有限公司)全球范围内制作与发行。
版权所有,侵权必究
客服热线:+ 86-10-68995265
客服信箱:service@bbbvip.com
官方网址:www.bbbvip.com
新浪微博目录 译者序
前言
第一部分 古代时期:1950年之前
第二部分 古典时期:1950~1980年
第三部分 现代时期:1980年之后
注释
人名对照表纪念与追忆
金融经济学思想的荣誉译者序
英国著名的史学家柯林武德提出:一切历史都是思想史,历史学
的任务就是要重演过去的思想。当现在的出版界充斥着讲述财富故事
的书籍之时,当人们将精力更多地放在这些传奇故事之时,普罗大众
往往在浮躁的喧嚷中忽略了故事背后的思想,从而落入了只见树木不
见森林的视角陷阱。马克·鲁宾斯坦所著的这部《投资思想史》犹如
一股清泉,令人耳目一新。“现值”的思想是如何出现的?“MM”理
论背后的思想真正源自何时?卖空机制为什么是有助于稳定市场的?
投资泡沫是如何破灭的?当前流行的投资概念是如何演进的?几乎投
资学中所有核心性理论都被囊括在这部思想史中。该书可被视做一张
投资思想史全景图。
18世纪法国启蒙运动的著名思想家伏尔泰认为,对于历史人们不
应该只以堆积史实为能事,还应该达到一种哲学理论的理解境界。
《投资思想史》很好地做到了这一点。该书从1202年斐波纳契的《算
经》开始写起直至2005年的行为金融思想,时间跨度800余年,内容相
当庞杂。但是读者自该书的目录开始全然没有混乱无序之感,这在很
大程度上得益于作者深厚的学术功底与高超的写作技巧,同时更离不
开作者对分散、独立事件的解读与重构。不过,在卷帙浩繁的投资学
文献中梳理出一条清晰的脉络还是需要非凡的智慧和很大的勇气的。
《投资思想史》的作者马克·鲁宾斯坦在金融学界久负盛名。他的学
术文章多见于《金融学学刊》(Journal of Finance)和《金融经济
学学刊》(Journal of Financial Economics)等顶级刊物。能在这
些顶级刊物上发表文章的学者不在少数,但能将投资理论的发展历程
娓娓道来的学者可以说是凤毛麟角。在《投资思想史》中,他以坚韧
的努力对一手文献进行搜集考据,他以宏大的气魄将800年投资思想史
进行断代划分,他以卓绝的文笔对大家思想进行功过评价。通读全书
不禁让人感叹:“洛阳三月花如锦,多少工夫织得成?”
对于学者而言,该书堪称是一部参考文献手册。全书引用了上百
篇经典文献,每篇文献都有详尽的出处,这对学者开展相关研究甚有
帮助。鲁宾斯坦对投资学历史中出现的基础性概念与核心性思想的解
读也将有助于学术研究者把握这些内容的来龙去脉。相信该书能为投
资理论的基础性研究在中国的传播与创造有所裨益。对于投资实务界人士而言,该书有助于投资思维的升华。时至今
日,全球正面临着百年一遇的金融危机。历史经验告诉我们,危机中
往往孕育着机会。然而,机会的把握往往需要过人的智慧。《投资思
想史》虽然不会直白地告诉您如何去投资,但它会帮助您站在费雪、凯恩斯、哈耶克、阿罗、萨缪尔森和弗里德曼等大师的肩膀之上去审
视投资。
当然,对于任何一部著作我们都应抱着批判的心态去阅读。《投
资思想史》虽是大家之作,内容丰富,但它不可避免地存在着潜在的
不足。例如,该书对现代投资思想着墨偏少,尤其在行为金融方面显
得有些过于吝啬。当然,这与作者对行为金融范式的认知与一般学者
可能存在差异有关。再者,读者需要注意的是作者对某些思想的评论
只是一家之言,对于鲁宾斯坦的评论我们也应有自己的判断。
本书在中国内地的出版要感谢机械工业出版社华章公司的颜诚若
女士、王洪波女士的慧眼识珠与辛劳工作。当然,文章翻译方面的潜
在错误由译者承担。欢迎读者批评指正,我们的电子邮箱是:
junya@126.com.我们一定会虚心学习!
人类善于忘记历史,长期以来金融学这门显学也不能避免遭
此“厄运”。然而,投资归根结底是思想者的活动。那些有意在投资
学界或投资实务界大展宏图的人士应将这部《投资思想史》作为一把
开启投资思想的金钥匙。一部波澜壮阔的投资思想史即将在您的面前
展开,愿您能以“闲坐小窗读《周易》,不知春去几多时”的心境品
读欣赏!
张俊生前言
思想很少着衣而诞,而是在艰苦的累积过程中逐渐穿上华美的衣
物。在人文艺术的许多领域,为了能更深入地获取知识,有必要知道
这个领域的思想是如何演进的:这些思想是如何产生的?如何走向成
熟的?一个思想是如何催生另一个思想的?知识环境是如何滋养思想
的成长的?为什么现在看起来十分明显的思想曾让人感到十分困惑?
在社会科学中思考这些问题具有特殊的意义。在人文科学中,年
代进程是没什么意义的。例如,谁能说过去3个世纪的英国诗歌或戏剧
会超越莎士比亚的著作?在自然科学中,可以通过发现先在和永续的
自然过程而获得知识累积。然而,社会科学中的知识被发现之后可以
影响社会演进,且在相互作用中决定着后续的社会理论。
基于这种精神,我呈现在大家面前的是投资金融理论的年代发展
进程中的参考书目。不过,这不是一部投资实践史,只是偶尔会引用
到金融理论以外的现实世界。这部“投资思想史”涉猎内容广泛,包
括方法论的发展和创造理论所使用的理论工具(包含经济学、数学、心理学和科学方法)。我正在写一部将耗时多年的书卷,名曰《西方
文明史纲要》(My Outline of Western Intellectual History),这部书也将历史回溯到古代时期。
尽管这本书可作为参考书,但也可以作为一部史书从头至尾地阅
读。书中大部分内容并没有按照专题来归纳,这是因为我努力将其当
做一个完整的领域来看待,并强调一类研究是如何影响其他研究的,而以前它们可能被认为是割裂的。为了这个目的,采用编年体的形式
看起来是比较恰当的,因为后来出现的思想不能影响先前出现的思
想,而只会相反。
我们可将金融经济学的历史分为三个阶段:①1950年之前的古代
时期;②1950~1980年的古典时期;③1980年之后的现代时期。大约
在1980年之后,古典时期的理论基础面临越来越多的挑战。
在大量的金融研究中,我只能选择很小比例的文献。有些文章之
所以重要是因为它们撒播下了思想的种子,提出了正确的问题,或者
发展了重要的经济直觉;有些文章则在不同思想之间进行了十分有效
的沟通;而另外一些文章之所以重要是因为它们将早期的概念定形、理顺假设并用数学给予支持。尽管我努力在这三类研究中做到平衡,但我还是将更多笔墨放在了前两类研究上。未发表的手稿只有满足如
下两个条件之一才被编选入内:①被广泛地引用;②在其他作者公开
发表的论文出现很久之前,其包含的思想就在该手稿中出现。如果某
些文献回顾对解释思想的渊源有帮助的话,我也会将其收录在内。对
一些重要结论的数学解释或证明也在书中有所展示,它基本上是对文
字模糊表述的补充。不过,这些证明对理解来说并不是必需的。
读者也应该理解本书还有很多工作要做。许多重要的研究未被提
及,并不是因为我认为它们不重要而是因为我还没有获得这些文献。
因此,这部史书是不完整的,尤其是1980年后的内容还有很多欠缺。
尽管本书将非理性主义者的思想追溯到古代与古典时期,但是本书对
现代日益丰富的“行为金融”文献提及甚少。不过,出版商还是鼓励
我整理手头已有的文献,因为他们感觉即便这类著作还处于发展时期
但还是十分有用的。希望本书的新版本将能弥补这个缺陷。
投资理论的历史发展得益于许多著名经济学家的著作。20世纪的
经济学家,如弗兰克·奈特、欧文·费雪、约翰·梅纳德·凯恩斯、弗里德里希·哈耶克、肯尼思·阿罗、保罗·萨缪尔森、米尔顿·弗
里德曼、佛朗哥·莫迪利亚尼、杰克·赫希雷佛、詹姆斯·托宾、约
瑟夫·斯蒂格利茨、罗伯特·卢卡斯、丹尼尔·卡尼曼、阿莫斯·特
沃斯基以及乔治·阿克洛夫都留下了他们的印记。一些非经济学家在
这个世纪也对金融学贡献颇丰,包括约翰·冯·诺伊曼、伦纳德·萨
维奇、约翰·纳什、莫里斯·肯德尔。进一步向前回溯,尽管丹尼尔
·伯努利和路易斯·巴舍利耶的贡献已经广为人知,但是像斐波纳
契、布莱斯·帕斯卡、皮埃尔·费马、克里斯汀·惠更斯、亚伯拉罕
·棣莫弗、埃德蒙·哈雷这些人的著作还鲜为人知但又十分重要。
可能这个领域与其他领域一样面临着学者忽视思想渊源的问题,我对此感到沮丧。尽管一些学术文章和著作声称是历史回顾,但还是
经常过于简单地描绘成熟理论的发展轨迹,而将太多原创性思想只归
功于少数学者。无疑本书也可能存在这样的缺陷,但我希望问题没有
以前那么严重。一本著作可能淹没在逝去的历史之中,甚至有可能这
本著作要比后来出现的且广为引用的文章都要优秀。
例如,问问你自己是谁最先提出了下列思想:
现值MM定理
普拉特-阿罗风险规避指标
马科维茨的均值-方差投资组合理论
戈登增长公式
资本资产定价模型
布莱克零贝塔模型
考克斯-罗斯-鲁宾斯坦的二叉树期权定价模型
卢卡斯交易模型
米尔格罗姆-斯托克利无交易定理
从个人理性假定推出预期效用
风险中性概率下的鞅定价
动态完整
随机游走与理性市场的联系
用非平稳方差来描述证券价格的随机过程
上偏股价、异质信念与卖空约束之间的假设关系
规模效应
超常盈余增长模型
前景理论
在上述大多数例子中,思想出现的实际时间要比一般人所认为的
起源提前许多年,偶尔会提前几十年甚至几百年。在某些情况下,独
立且近乎同时的发现者却很少甚至从未被提及,这多少证明了斯蒂芬
·施蒂格勒的得名法则,即科学思想从未以其最初发现者的名字来命名。包括施蒂格勒法则自身也是这样,该法则最初的提出者实际是社
会学家与科学哲学家罗伯特K.默顿。金融经济学中的一个著名例子就
是MM定理,其实在莫迪利亚尼和米勒提出该命题的前20年,约翰·伯
尔·威廉姆斯就在1938年出版的著作中做了精彩的探讨。如果这项创
新性的洞察能在当时广为知晓且得到仔细研究,那么我们受困扰的时
间就可以减少几十年。有关默顿的另一个例子是“戈登增长公式”。
不幸的是,一旦这类错误发生就很难纠正。事实上,这个错误已经根
深蒂固,即便是最杰出的著作也未必能改变业已形成的习惯。
此外,研究者可能没有意识到某些理论的基础工作在多年前就已
经被发现。一个著名的例子是布莱克-斯科尔斯期权定价模型。尽管这
个模型是在20世纪70年代得到发展的,并且无疑是金融经济学中最为
重要的发现之一。但事实上,肯尼思·阿罗在20年前的1953年就已经
提出非常类似的观点。反过来,阿罗的想法在3个世纪之前布莱斯·帕
斯卡与皮埃尔·费马之间的通信集中隐隐地有所体现。一个科学领域
的进步通常会借鉴其他领域的方法,尤其是原本用于其他目的的数学
工具。历史研究的副产品之一就是能发现原本看似无关的工作之间的
联系。
有人会问,为什么学术领域会对自己的渊源不求甚解。历史是由
胜利者重新书写的。学生经常依赖于自己的导师来了解学科历史,而
导师又过分依赖于他自己的导师,依此类推。很少有学生会拒绝现存
的引用方式,而去图书馆书架上翻找古旧书籍和期刊来寻找他们所使
用思想的真正渊源。学者与大多数人一样,他们偏爱将成就归因于那
些相对出名的人或那些在发展这个思想方面写了几篇文章或花了数年
时间的人,而那些非主流的人士(可能是使用的方法或时机方面)即
便研究的更早更原创,还是处于不利的位置。绝好的一个例子就是
A.D.罗伊在均值-方差投资组合方面的基础性文章,就连哈里·马科维
茨也承认希望自己能与罗伊共享投资组合理论之父的荣誉。1罗伯特K.
默顿将之称为“马太效应”。这个典故来源于《马太福音》(第25章
第29节):“因为凡有的,还要加给他,叫他有余;没有的,连他所
有的,也要夺过来”。
当然,并不只有金融学才倾向于忽视自己的起源。例如,算术被
认为是艾萨克·牛顿和戈特弗里德·威廉·莱布尼兹发明的。但事实
上算术的发明可以追溯到古希腊时期。尤其是安提丰、欧多克斯、阿
基米德在使用“穷举的方法”的时候预期到了可采用极限和积分的概
念来决定几何物体的面积和体积(例如,估计圆的面积时,在圆中镶入正规多边形,随着多边形的边数无穷增加,多边形就可以近似估计
圆的面积)。尽管伽利略并没有用数学公式来正式表示,但他有关物
体运动的著作已经暗含如下内容:物体的运动速度是距离相对于时间
的一阶导数,加速度是距离相对于时间的二阶导数。皮埃尔·费马设
计出了正切法,今天我们仍在使用这种方法,它可用于判定函数的最
大值和最小值。艾萨克·巴罗使用微分的方法去寻找一个曲线的切
线。并提出了两个函数的乘积和商的微分定理、X的幂函数微分定理以
及隐函数的微分定理。
与大多数历史不同,有关金融学思想起源的大多数被遗忘的事实
都能在那里等待我们的发掘,在图书馆书架上的古旧书籍中,在过去
的期刊中(现在大多可以以电子版形式获得)我们都能发现这些思
想。很多投资理论史只是被胜利者重新书写过,最初雏形被修正过而
已。在本书中,我会竭力去探究这些思想的渊源。对于书中所引用到
的每一篇文章、每一本著作,我的目标都是明确它们对这个领域的边
际贡献。
如同莎士比亚名著《麦克白》中的三个女巫一样拥有后见之明,我能“窥视时间的种子,能说出其中哪一粒能发芽,哪一粒不能成
长”。拥有了这项优势,我在那些曾一度被认为很有前景但最终被证
明是死胡同的研究上(例如股价的稳定帕累托假设)没有花费太多精
力。
不过,我自知本书省略了许多十分重要的发现(部分原因是因为
我还没有得到这些文献)或可能将投资思想追溯到不正确的源头,可
能并没有发现更早的著作。另一方面,我也可能犯历史学家惯有的毛
病,即用后世看起来重要或正确的观点来解释书面记录,这可能是有
偏见的。我希望读者能够原谅我。我也从默顿·戴维斯那里获得了一
些帮助,为此对他表示公开的致谢。我也请求读者能提出建设性的意
见让我知晓错误,以便在以后的版本中修正。
马克·鲁宾斯坦
加州,伯克利
2006年元月第一部分 古代时期:1950年之前
1202年
斐波纳契或称比萨大公(1170—1240)出版了《算经》(Liber
Abaci)一书。该书最近由劳伦斯E.西格勒翻译成《斐波纳契的算经:
比萨大公算经的现代英译本》(Fibonacci's Liber Abaci:A
Translation into Modern English of Leonardo Pisano's Book of
Calculation)(Springer-Verlag,2002年)。1478年
未 知 名 的 作 者 出 版 了 《 翠 维 索 算 术 》 ( The Treviso
Arithmetic)一书。该书由戴维·尤金·史密斯翻译成英文,见弗兰
克J.施维茨所编著的《资本主义与算术:15世纪的新数学,包括1478
年〈翠维索算术〉全文》(Capitalism and Arithmetic:The New
Math of the 15th Century Including the Full Text of the
Treviso Arithmetic of 1478)(LaSalle,IL:Open Court,1987
年)。1761年
埃德蒙·哈雷(1656年11月8日—1742年1月14日)所著的《论复
利》(Of Compound Interest)在哈雷逝世后出版。见亨利·舍温编
著的《舍温算表》(Sherwin's Mathematical Tables)(W.and
J.Mount,T.Page and Son,1761年)。
斐波纳契数列、现值、合伙制、永续年金、资本预算
斐波纳契(1202)因为将阿拉伯数学符号引入欧洲而闻名于世。
阿拉伯数字最早可能于公元后第一个千年的中期形成于印度,其后逐
渐被阿拉伯商人和学者所学习。斐波纳契在北非的旅行中学到了阿拉
伯数字。在书中的第一章,他是这样开篇的:
如下是印度人使用的九个数字:9,8,7,6,5,4,3,2,1。用
这九个数字,再加上0这个符号,任何数字都既能被书写也能被示范。
在这本小册子出版后,用笔墨计算的阿拉伯数字取代了算盘的地
位。这本书也提出了著名的斐波纳契数列,1,1,2,3,5,8,13,…
《算经》这本书在现值计算发展中的作用却没有得到足够的重
视,直到最近才被威廉N.戈茨曼发现 [1]。斐波纳契通过几个数学例子
来说明他的计算方法。其中对投资学有四个方面的应用:①在合伙人
成员中进行公平的利润分配 [2];②序列投资的利润计算,其中包括中
间撤出投资 [3];③终值的计算 [4];④现值的计算 [5]。他对问题①的
解答很简单:将利润按照投入资本的比例来分配,这个答案在今天看
来是显而易见的。关于问题③的举例,西格勒是这样翻译的:
有个人在一家银行存入100英镑,每英镑每个月能获得4便士的利
息。他每年取出30英镑。那么他需要花多少时间才能把钱全部取出
来?(p.384)
斐波纳契的计算结果是,那个人的钱在银行的时间是6年零8天零
(12)(39)5个小时。上述表达式是斐波纳契所使用的符号,按照
今天的表示方法每一部分的分母应等于该分母与所有右边分母的乘
积,如12实际上表示的是(12×19)而小时数就是所有部分的加总和。因此,按照现代的符号表示的小时数等于5小时+(39)小时
+(118)小时= 小时。值得注意的是,尽管斐波纳契的符号
已经被废弃,但当度量小数量单位时还是很有用的。例如,斐波纳契
将会这样来表示5周零3天零4小时零12分零35秒:(3560)(1260)
(424)(37)5。
在问题④中,斐波纳契通过对两只年金现值进行排名的方式演示
了现值的使用。两只年金的区别仅在于获得报酬的周期不同,利息再
投资的利率都是每个季度2%:两只年金每年都各支付300个金币,不同
在于其中一只年金每季度支付75个金币,而另外一只年金则在每年年
末支付300个金币。
由于复利的存在,固定利率下的现值是几何序列的加权求和。戈
茨曼推测,斐波纳契的利息概念可能为他提出著名的无穷级数概念提
供灵感。不幸的是,我们对斐波纳契知之甚少,这样的猜测还不能被
证实。
在斐波纳契之后,阿拉伯数字在欧洲得到广泛的使用,尤其是用
于商业目的。一位不知名的作者所著的《翠维索算术》(1478)是迄
今已知的最早的算术书,它试图普及阿拉伯数字系统。该书在开篇描
述了如何使用阿拉伯数字来计数、加、减、乘、除——这与今天使用
的程序是一样的。在那个时期,数字刚刚演化成现代所使用的形式。
例如,用 表示零的方式在1275年后销声匿迹。其中部分原因可能
要归因于《翠维索算术》,因为印刷技术可能迫使书写标准化。不
过,加、减、乘、除等符号要到很晚才被引入。“+”和“-”出现
在1489年,“×”出现在1631年,“÷”出现在1659年。既然谈到这
个问题,我们就展开一下。“√”出现在1525年,“=”出现在1557
年,“<”和“>”出现在1631年,“∫”出现在1675年(由戈特弗
里德·威廉·莱布尼兹发明),“f(x)”出现在1735年(由列昂哈
德·欧拉发明),“dxdy”于1797年由约瑟夫-路易斯·拉格朗日提
出。用小数表示分数直至1585年才出现。用字母表示等式中的未知数
直到1580年左右才在弗兰克斯·韦达(1540—1603)的公式中出现。
约翰·纳皮尔于1614年发明了对数,并在1617年将小数符号引入欧
洲。这些数学运算是通过一些事例来演示的。合伙制可以追溯到公元
前2000年的巴比伦王国。这种商业组织形式为长期需要大笔资金的投
资提供了一种融资方式。在信奉基督教的欧洲,禁止放高利贷收取利
息,合伙制则提供了一种迂回的方式。《翠维索算术》这本书中
(p.138)提出的第一个合伙制问题是这样的:
有三个商人共同搭伙投资。第一个人名叫皮耶罗,第二个人名叫
保罗,第三个人名叫朱安妮。皮耶罗投入112个杜卡托,保罗投入200
个杜卡托,朱安妮投入142个杜卡托。过了一段时间,他们发现已经赚
了563个杜卡托。问每个人应分多少个杜卡托才是公平的。
建议的答案是:根据他们各自的投资额按照比例来分配利润。这
个原则与斐波纳契在《论公司》提出的原则一样。第二个合伙制问题
更有趣(p.138):
有两个商人,分别叫做桑巴斯提亚诺和贾科莫,他们合伙投资来
赚钱。桑巴斯提亚诺在1472年1月1日投入了350个杜卡托,贾科莫在
1472年7月1日投入了500个杜卡托和14个格罗西。到了1474年1月1日,他们发现已经赚到了622个杜卡托。问每个人分多少?
首先将每个人的投资转换为同一计量单位,即桑巴斯提亚诺投入
8400个格罗西,贾科莫投入12014个格罗西。《翠维索算术》这本书通
过两人各自的投资月数来调整投资时点的差异:
桑巴斯提亚诺:8400×24=201600贾科莫:12014×18=216252
而 后 根 据 各 自 所 占 的 比 例 来 分 配 。 两 数 之 和 是
201600+216252=417852 。 因 此 , 桑 巴 斯 提 亚 诺 获 得
622× ( 201600417852 ) =300 杜 卡 托 , 贾 科 莫 获 得
622×(216252417852)=322个杜卡托。
现代的分析师要解决这个分配问题需要区分两种情况:贾科莫的
滞后投资是事先约定好的呢,还是在临近投资时才决定的。在第一种
情况下,他应当知道利率才能计算出公平的分配利润;在第二种情况
下,他应当知道1472年7月1日那天合伙体中每股的价值。尽管《翠维
索算术》的作者提出了一个有趣的问题,并且可能从斐波纳契那儿学
了不少东西,但是他的答案表明他并没有理解斐波纳契复杂的现值分
析。到了16世纪,尽管高利贷在法律上受到限制,但斐波纳契有关现
值的著作仍得到了更好的认知。例如,吉恩·川辰特于1637年 [6]提出
了这么一个问题:一只永续年金每季度支付4%的利息,而另外一只定
期年金每季度支付5%的利息共计41个季度,问哪只年金的现值最高?
川辰特是这样解决这个问题的:首先计算每季度1%的年金在第41个季
度的终值,接着计算从第41季度开始每季度支付5% [7]的永续年金在第
41季度的现值,将两个数字比较后就能知道哪只年金的现值最高。在
川辰特的书中还包含了第一张现值折现因子表。
在没有计算机的远古年代,要判断利率对合约的影响,那么一定
要在快速计算方法上花大工夫。这包括使用对数、算表以及现值问题
的现成答案。埃德蒙·哈雷通过望远镜观察对南半球的星体进行了编
撰归类,发明了第一张气象分析表,出版了早期的人口死亡率表,当
然最著名的是他首先计算出彗星的轨道。他在金融经济学方面的贡献
也颇为称道。哈雷(1761)推演出年金现值公式(可能并不是最先推
演出的):[X(r-1)][1-(1r T)],这个年金开始于第一年年
末,持续期是T年。r表示1加上年利率,X表示从年金中每年获得的现
金额。对这个公式相对较早的另一个推演版本可以在费雪的作品中找
到(1906)。
尽管用现值来估值出现的比较早,但最先提出任何资本项目都应
当使用现值来评估的思想可能要归属费雪(1907)。使用套利的思
想,他对项目现金流与证券投资组合现金流进行了比较,其中证券投
资组合现金流是与项目相匹配的。不过,根据福尔哈伯和鲍莫尔
(1988)的说法,无论是《哈佛商业评论》从1922年创刊到第二次世
界大战,还是1948年前使用的公司财务方面的教材都没有在资本预算
中提到过现值。直到约尔·迪安(1951)的著作出版 [8]之后,现值的
使用才广为流行。最近,根据约翰R.格雷厄姆和坎贝尔·哈维
(2001)的研究 [9],大多数大型企业在资本预算决策中都使用一些形
式的现值计算。1494年
卢卡·帕乔利(约1445—1517)出版了《算术、几何与比例学总
论 》 ( Summa de arithmetica , geometria , proportioni et
proportionalita)(Everything about Arithmetic,Geometry and
Proportions)一书。其中,有关会计学的内容见《详论会计与记录》
(Particularis de computis et scripturus)。由A.冯·贾巴斯塔
托翻译成英文,见《卢卡·帕乔利对复式记账的探索:威尼斯1494》
( Luca Pacioli's Exposition of Double-Entry Bookkeeping :
Venice 1494)。
点数问题、会计、借与贷、会计恒等式、资产、负债和权益、净
盈余关系、账面价值与市场价值、配比原则、一致性原则
帕乔利(1494)承认他借鉴了欧几里得(约公元300年 [10])和斐
波纳契(1202)的思想归纳了算术、代数、几何和三角学的基本原
则。对我们来说更为重要的是,帕乔利提出了“点数问题”,他因此
而广受赞誉。“点数问题”最终促成了现代概率论在17世纪的爆炸式
发展(当然也有证据表明这个问题的起源可能会更早些):
选手A和选手B正在打球赛。他们同意直到一方赢得6局时就停止。
但比赛在A赢得5局B赢得3局的时候停止了。问如何分配赌注?
帕乔利的答案很简单(但不正确):根据每个人所赢的局数来按
比例分配。因此,如果赌注是56个金币,那么选手A应获得35个金币,选手B获得21个金币。
不过,帕乔利的书因其对会计的影响而闻名。古时候的会计只是
简单地列示出存货的物理量。后来会计方法把这些项目按照单一货币
的形式统一成共同的度量单位。这就变成列示“入账”和“出账”,本质上是一张说明现金来源和使用的现金表。这样一来,封建领主就
可以监督分发财物的管家。现代形式的复式记账的起源可不是很清
晰。我们知道在意大利的西耶耶(Siena)有一家名叫加勒尼
(Gallerani)公司的商业企业早在1305年就使用了复式记账的方法 [11]。尽管帕乔利并没有发明复式记账法,但是由于他在这部影响深远
的著作中深入地阐述了复式记账法,因此他通常被视为这种方法的创
始人,并被尊称为“会计学之父”。在他这本书中有关会计学内容的部分,即“详论会计与记录”这部分内容,帕乔利写道:“这种威尼
斯人所使用的方法是诸多方法中最受推崇的,并可将其当做其他方法
的指南”(p.42)。他甚至训诫会计师,如果他们的账目借贷不相
等,那么晚上都睡不安生。对财务会计习俗史的进一步讨论已经超出
了本书的意图。但是,由于会计概念对于测量公司证券的预期收益和
风险都十分重要,因此我还要讨论几个关键性问题。
首先,外部财务报表的目的是什么?在我看来,外部财务报表的
目的是为股东提供信息。可能有人认为,财务报表还应该为公司员
工、供应商以及债权人提供信息:员工根据财务报表评估自身人力资
本投资于公司的风险与收益,供应商根据报表评估与公司做生意的风
险与收益,而债权人则根据报表评估公司的违约风险。但我认为,既
然股东是公司所有者,他们通过影响公司股价从而间接为公司做出资
源分配决策,因此,财务报表的主要使用对象是公司股东。虽然财务
报表还有其他目的,但其首要目的是帮助股东判定公司股票价格。这
一观点与金融经济学中的基本观点“企业应为股东谋取利益”一致,也受到法律的认同。在实践中,虽然员工、供应商以及债权人能获取
有关公司的其他信息,但为股东编制的年报(包括资产负债表和损益
表)则是他们获取信息的重要来源,对大型上市公司尤其如此。
企业要履行为股东提供信息的义务,一个办法就是将每个员工全
年的工作情况拍摄下来,集合起来寄给每位股东。这样,股东就能没
有偏差地全面了解当年的实际情况。但是,这种做法显然是很荒谬
的。还有另一种极端的做法,就是企业每年年末只给股东提供一个数
字——企业对自身股价的估计值。这种方法也同样不可取,因为企业
没有足够的信息对股价做出准确的评估。正如哈耶克(1945)指出
的,影响公司股价的因素通常广泛分布于整个经济体中,没有哪个小
部分个体甚至企业所有员工拥有足够信息对公司股价做出有效的估
计。撇开信息量不说,即便你拥有足够的信息,用什么方法将信息糅
合进股票价格也不明确,更不能指望企业会知道如何做。企业可能出
于利益的关系,故意过高估计股价,以此来操纵企业从投资者手中获
得的资源或者调整管理层的激励报酬方案。另外,企业还面临一个约
束,不能发布那些削弱他们与其他企业相互竞争的动力信息,尽管这
种信息可能有助于股价评估。因此,会计的难点就在于找到一种折中
的办法,既要能概括一年中发生的事情,同时又不能泄露任何重要的
信息,不能指望企业完全诚信,亦不能损害企业的竞争动力。从帕乔利开始人们就一直在思索解决上述难题的办法,最终想出
的办法就是提供两张财务报表:资产负债表和损益表。第一张表,资
产负债表,就像一张快照,捕捉了公司在某一特定时点的相关信息。
第二张,损益表,像一部电影,演示了企业的资产负债表是如何从前
一个时点变到另一个时点。资产负债表反映了所有导致资产发生变化
并相应引起负债或股东权益发生变化的交易(有时是某些权益与负债
的互换或者一项资产换成另一项资产)。这让我们得到复式记账法的
基本原理、赫赫有名的会计等式:
资产=负债+所有者权益 (1-1)
任何交易都有两方面影响,如同时增加资产与负债,或增加某类
资产的同时减少另一类资产,最终保持等式成立。通常资产被划分为
三类:第一是流动资产,包括现金、应收账款、存货以及预付费用
等;第二是长期有形资产,如厂房、设备等;第三是长期无形资产,如研发费用的资本化价值以及著名品牌价值。负债分为短期负债与长
期负债两类:短期负债包括应付账款、递延税收与短期债务;长期负
债包括长期银行债务、公开发行的企业债券等。所有者权益分为实收
资本与累积盈余两项。损益表将各项费用扣减各项费用后得到利润,这部分利润是企业在两张资产表所在时点构成的时段内获得的利润。
如果用利润除以发行的股份总数,就得到每股收益(EPS)。企业财务
报表还会单独报告发放股利占利润的比例,用以计算每股股利。
如果投资者只想用一个数据来说明问题,那他可以只看每股收益
指标。该指标是会计师对两张资产负债表时点之间企业股价本应变化
多少的一个估计(加上股利)。也就是说,假设S t-1和S t分别是在时
点t-1和时点t的股价,D t是每股股利,而X t是两时点之间报告的每股
收益,则
(S t+D t)-S t-1=X t (1-2)
如果会计师与股票市场都是理性的,那么股票价格的变化应该正好满
足这个等式。
而且,使用上述EPS等式以及所谓的净盈余会计关系(假定没有新
增实收资本),则
Y t=Y t-1+X t-D t (1-3)我们可以证明每股股价S t等于对应的每股账面价值Y t。我们从时
点0企业的初始状况开始,S 0=Y 0,账面价值Y 0为实收资本。我们可
以得到如下递归等式:
事实上,即便市场是有效运转的,大多数公司的市场价值与账面
价值也不相等。虽然我们有理由责怪会计师们,他们处理账务时也是
左右为难。比如,有时候企业在卖出产品之后数月才收到货款、支付
费用,而有时候企业在产品卖出去之前就提早收到现金或支出现金。
如果简单地把当年发生的所有交易都记为收入或者费用,会让人产生
误解。而会计的“匹配原则”要求只有当年已经销售出去的产品所带
来的销售收入以及生产这些已销售产品所产生的费用才能记入该年的
损益表。与当年已销售产品不匹配的现金流入或现金支出则以某种形
式进入资产负债表,通常等到来年产品销售出去之后再进入下一年的
损益表。这称为“权责发生制”,与“现金收付制”不同。现金收付
制用现金流出匹配现金流入,而不是用费用匹配收入。会计师们面临
这样的权衡:使用现金收付制能提高报表的准确性,而使用权责发生
制能提供更为有用但可能不太准确的信息。对于编制外部财务报表而
言,会计师们更倾向于权责发生制。
举个简单的例子,资产负债表上之所以有存货一项就是因为存在
匹配原则。存货反映的内容可能是已经采购但尚未投入生产的原材料
或者尚未销售给顾客的产成品。这样,如何记录存货的成本又是一个
会计问题。比如,如果企业同一种存货是分批以不同的价格采购进
来,那么那些已制成产成品并销售出去的部分存货应该如何计算费用
呢?一种方法是假定先采购的存货先使用,即先进先出法(FIFO);
另一种方法是假定后采购的存货先使用,即后进先出法(LIFO)。
再看个稍微复杂点的问题。假设企业购买了一台使用寿命较长的
生产设备,该设备将在较长一段时间内慢慢损耗,最终技术上将过
时。根据匹配原则,企业需要确定每年为了生产那些已销售的产品,设备损耗了多少。虽然我们知道设备的原始采购成本,也知道几年后
如果将设备售出能获得多少收入,但我们很难找到一个完美的方法来
确定该设备每年具体的折旧率。因为没有交易能证明折旧费用的具体
金额。于是会计师们以他们最中意的方式解决这一难题。他们假定设备每年都以某个固定的折旧率折旧,当然这个折旧率取决于设备的类
型。这种简单的方法称为直线折旧法。如果设备使用10年,那么每年
记入设备费用的就是采购成本的10%。不过,直线折旧法并不能准确反
映设备的折旧情况,往往设备在最初使用年份折旧较快而之后折旧较
慢,于是会计师们有时采取加速折旧法。一方面,会计师们希望能给
企业一定余地让它们能更好地匹配收入与费用,但同时,他们又担忧
如果弹性过大,企业可能会借此误报(通常是夸大)收入。所以会计
师们总是努力找到平衡点。也正是因为这种平衡行为使得会计工作更
加富有趣味,而所谓的常规也不再一成不变。
尤其复杂的是如何分配研发费用、营销费用与广告费用。应该先
将它们资本化再慢慢转为成(摊销)费用呢,还是应该立即记为费用
呢?要回答这一问题,我们需要解决一个非常复杂的难题:这些费用
到底在多大程度上影响那些不在费用发生当年而是在随后年份销售的
产品所产生的收入与费用?
上述例子引出了另一个会计原则:由于股东将使用会计信息预测
未来的收入与费用,因而财务报表需要让股东能非常轻松地判断哪些
收入与费用是由于企业持续经营产生的,哪些是因为某一次特殊情况
所产生的。为了实现这一目的,企业的利润与损失通常被划分为两
类:一般损益与非经常性损益。非经常性利润来自预期之外的企业资
产与负债价值的变化。我们有必要区分如下三种非经常性利润:①由
非企业掌控因素变化带来的利润,如利率波动会影响企业负债的现
值;②企业在日常经营之外的有意决策所带来的利润,如企业决定持
有日元现金而不是美元现金;③由于事后对早期会计报表的更正而带
来的损益,如由于产品需求发生变化而导致存货滞销,这部分存货不
再用于销售因而给企业造成损失。遗憾的是,最后一类往往说明企业
在前几年没有很好地遵守匹配原则。不过,出于估值的目的,我们还
是越早知道这类的坏消息越好。
另一个要解决的会计难题是应该简单报告已实施交易的结果呢,还是不断修正这些结果以反映市场价值的变化呢?例如,一家水果企
业最重要的资产就是它在1900年以100万美元购置的一块地皮。在购置
之初,资产负债表上显示资产价值100万美元。过了一个世纪,随着旅
游业的飙升,该地皮的价值已经逐渐上升为1亿美元。假设现在企业其
他资产的价值与该地皮相比已经微不足道。如果企业的资产负债表依
然显示该土地的价值为100万美元,那么股东就无从得知如果企业将土
地卖掉就可以获得高额收入。显然,企业需要每年都更新土地的市场价值,价值的变动以非经常性损益列示。这样,资产负债表上的资产
和所有者权益都将发生相应变化:土地的价值为1亿美元,同时所有者
权益增加9900万美元。不过,市场会计价值法在解决一个问题的同时
又带来一个新问题:既然土地还没有卖出去,企业又如何知道它到底
价值几何呢?虽然这种不确定性可以通过多种方式降低,但没有办法
完全消除。如果不确定性不能消除,那么以市场价值为基准的记账法
就不如以实际交易为基础来得准确。股东也希望区分未售出土地的未
实现收入与已售出土地的已实现收入。另外,只要土地尚未售出,不
同专家对其市场价值就会有不同的看法。股东应该相信哪个专家呢?
尤其是当企业管理层有动力夸大土地价值时,股东是否能够相信企业
聘用的专家呢?
公认会计准则(GAAP)为这一问题提供了全面回答:根据资产市
场价值的不确定性,某些资产和负债可以按照市场价值重新评估,而
其他资产则不可以。其他资产,如资本设备,既不是按市场价值也不
是按成本价格进行评估,而是严格按照某些设计好的折旧处理方式来
估计资产价值的可能损失。
导致前文描述公司股价与收益关系以及每股市场价格与账面价值
关系的等式不成立的原因有多个与估值相关的问题,上述例子只是其
中几个而已。最重要的原因可能来自行业竞争的结构性状况。在许多
行业,企业有能力建立垄断优势或寡头垄断优势,这些优势不受企业
账面价值影响。通常当产品需求尚未扩大时,只有少量企业会进入该
行业。这一现象使得先动优势非常明显。例如,曾开发出最受欢迎个
人计算机(PC)操作系统的微软公司曾为我们很好地展示了如何利用
自己独一无二的优势来主导PC软件应用行业。然而,即便微软的实体
资产是按市场价值记入财务报表,读者也无法从微软的所有过去交易
以及财务报表中预测到它的市场价值与账面价值的高比率。企业市场
价值与账面价值的差异不仅反映了企业当前极高经营利润率,而且还
体现了企业拥有在将来能带来高额利润的投资机会,这种投资机会是
其他不具备微软垄断优势的企业所不具备的。而股票市场不会自动等
待利润的到来,而是早就将这些利润反映到股价中;市场会预期企业
未来利润,从而导致企业的市场价值与账面价值出现重大分歧。
基于上述观点,金融学家把高MB(市场价值账面价值)比率的
企业称为成长型企业,而低MB比率的企业称为价值型企业。投资者可
以投资共同基金,某些基金专注于成长型股票,而某些基金专注于价
值型股票。我们希望上述讨论已经清楚解释了企业账面价值与市场价值出现差异的多种原因,但是用于区分成长型股票与价值型股票的MB
比率并不是完美的。
从历史角度来看,用于度量业绩的会计报表侧重于企业盈利水
平,这是一个收益指标。但是,从马科维茨(1952年3月)和罗伊
(1952)开始,金融经济学家们就开始认为,除了收益,业绩应该还
包含另一方面,那就是风险。虽说现在会计制度的设计并不是为风险
考虑(可能需要重新设计,使得风险度量更加容易),现代财务报表
仍十分有用。例如,根据连续的财务报表,我们可以得到每股经常性
收益的时间序列,据此算出收益的方差,而收益方差则是衡量股票投
资风险的一个独立指标。然而不幸的是,不少企业都想尽办法,利用
匹配原则的灵活性调整各期收入或费用,从而稳定收益波动,使得风
险看起来似乎较低。
用财务报表测量风险的常用方法为比率分析法。例如,最常见的
流动资产对流动负债比率就是衡量企业违约风险的硬性指标。息税前
利润(EBIT)与年利息额之比是违约风险的流量指标。长期资产对短
期资产比率反映了企业的流动性和估值风险,因为短期资产的流动性
较高,其价值的不确定性较低。虽说企业股票的风险来自多个方面,有企业内的因素亦有企业外的因素,但就企业内而言风险主要有三种
来源:①收入来源的分散化;②经营风险;③财务风险。
现在的财务报表本身并不能提供企业分产品或分行业的收入信
息,来帮助投资者了解企业分散化经营程度。投资者只能从报表附注
或者其他渠道如企业发行证券之初的注册报告中寻找此类信息。
经营风险可以定义为固定成本与变动成本之比。比率越高,企业
利润对收入变化的敏感程度就越高。虽然损益表并没有直接区分固定
成本和变动成本,但依据成本的种类就可以在某种程度上对成本进行
区分,而且将各项费用与收入进行时间序列的回归分析就可以判断哪
些成本是固定成本,哪些成本是变动成本。
反映企业财务风险的常见指标是负债与权益之比,二者都使用账
面价值。负债对权益比率越高,企业的杠杆越高,则企业线下利润对
息税前利润变化的敏感程度就越高。不过,权益的账面价值往往并不
反映权益的市场价值;而负债的账面价值与市场价值则较为接近。而
且,我们随时都可以根据股票市场股价的变化获得权益的市场价值。因此,金融经济学家喜欢用负债的账面价值对权益的市场价值之比来
度量财务风险。
然而,这种度量财务风险的方法也并非轻而易举。显然,作为前
提条件,交易必须归类到负债或者权益。出于度量财务风险的目的,负债的本质来自于企业承诺支付的固定偿还额。即便企业偿还了所有
债务,债务所有者也不能分享企业成功的好处。而权益则不同,权益
没有支付义务,但在企业偿还所有其他人(包括雇员、供应商、债权
人以及政府)之后,企业所有的剩余都归权益所有者所有。正是因为
拥有“剩余索取权”,企业的盈利能力将直接增加所有者权益。有些
证券,如优先股、可转换债券以及员工股票期权,属于混合证券,既
有负债的特征又有股票的特征。如何对它们进行划分是个难题。
一致性是另一会计原则:不同企业处理日常经济本质类似交易的
规则设计应该不影响对企业收益与风险的比较。1994~2005年美国发生
的针对员工股票期权的争议就很好地说明了一致性问题。假设有两家
类似的企业A和B,不同的是企业A只使用现金支付员工报酬,而企业B
则只使用股票期权,最初为平价发行的期权。为了使案例简单化,我
们假定两家企业从员工手中获得相同的服务。自然,企业A将现金报酬
费用化,那企业B应该怎么做呢?如果按照标准做法企业B不将股票期
权作为费用处理,那么它的利润就会较高,尽管从经济角度来看它和
企业A做着相同的事情,而且企业B的业绩也并不优于企业A。因此,一
致性原则要求企业B在授予期权时就要确定期权的市场价值而且将其作
为费用处理。
处理租赁资产的例子很好地说明了实现一致性原则的困难。设想
有两家类似的企业:企业A借钱购买了一幢大楼;而企业B则是租赁了
相同的建筑。在企业A的资产负债表上,会计师们通常将大楼的购置成
本作为资产入账,同时增加相应的负债。通过这种方式,大楼的添置
提高了企业的负债对权益比率以及负债对资产比率。而在企业B的资产
负债表上,如果租赁期比该大楼的全部寿命周期短,那么租赁资产的
价值就不会出现在资产负债表上,它只以租赁费用的形式影响企业的
损益表。按照这种方式,企业B的负债对权益比率以及负债对资产比率
都不会发生任何变化,因而看起来它的财务风险似乎低于企业A。这种
处理方式迥异的主要原因在于两种交易的法律实质大不相同。企业A拥
有大楼的所有权,而企业B却没有。但是,从财务分析的角度来看,这
只是形式的差异,经济本质并没有什么差异。如果金融经济学家熟悉
租赁,他会这样理解租赁:其实企业B与企业A的区别不过是企业B借的是整幢大楼而不是现金;它定期支付租赁费用(经过折旧调整后的)
而不是利息费用;而且企业B最终将偿还大楼,就像企业A也要偿还借
款一样。如果遵循一致性原则,企业B就应该像企业A一样处理租赁业
务,使得两家企业的负债权益比一样。一种方法就是企业B将租赁建筑
物的价值借记资产,同时贷记相同数额的负债,说明企业有义务“偿
还”该“借来”的建筑。
上述做法尽管听起来很合理,但进一步分析就会显示实现一致性
原则是多么费力的一件事。按上述方法处理租赁意味着资产并不是按
照法律所有权来界定,而是定义为被企业使用并带来收入的事物——
企业B并不拥有该幢大楼,但企业用其获得收入,因而从这种意义上说
租来的大楼构成企业B的资产。现在,这个一致性目标的确为我们带来
困扰。设想一下:两家企业都使用了总部大楼外的街道,员工每天上
下班都使用该街道;当员工出差时他们还使用了飞机的座椅;如此等
等。如果遵循一致性原则,这些街道、飞机座椅等都应该出现在企业
资产负债表上。理论上,金融经济学家希望企业这样做。但我们再比
较如下两家企业:一家企业通过债务融资自己买下了航空公司和道
路,而另一家企业则是使用别人提供的道路和飞机座椅。如果再使用
一致性原则比较这个极端例子,显然很不实际。
我们不应该过于夸大设计完美会计准则的重要性。外部会计报表
只不过是人们获取企业信息的一种渠道。某些个人,如专业证券分析
师,专注于研究某个行业,他们大量的时间都用于评估该行业的上市
公司。因此,即便会计准则出现错误,也只是我们了解企业基本信息
的成本增加而已,市场仍会很好地给企业股票定价。例如,许多企业
管理人员认为,由于将股票期权费用化会降低每股收益,一旦改变会
计处理方式,它们的股价会下跌。但是,市场有其他方式了解到企业
的期权计划,因而更可能出现的情况是企业股价不会受到会计方式变
化的影响。1654年
布莱斯·帕斯卡(1623年6月19日—1662年8月19日) 出版了
《 论 算 术 三 角 形 》 ( Traité du triangle arithmétique avec
quelques autres petits traités sur la měme matière)。同年,与皮埃尔·费马(1601年8月17日—1665年1月12日)写就《与费马在
概率理论方面的通信集》(Correspondence with Fermat on the
Theory of Probabilities),见《西方世界的伟大著作:帕斯卡篇》
( Great Books of the Western World : Pascal ) ( Franklin
Library,1984),pp.447~487。
帕斯卡三角形、概率论、点数问题、帕斯卡赌注
最早对组合问题的研究似乎始于印度 1。大约在公元1150年,婆什
迦罗就认识到了从j个数中取出n个数的组合数为n![j!(n-
j)!]。早在1265年,阿拉伯数学家图西就知道了二项展开式
(a+b) n的系数计算以及如何在三角形中排列展开式系数。中国数学
家朱世杰1303年出版的《四元玉鉴》也讲述了二项展开式的计算,该
书的扉页后来广为流传。法国的马林·梅森(1588—1648)在1636年
就懂得了组合恒等式与展开式系数之间的对等关系。
帕斯卡虽然不是算术三角形的发明者,但他首次著文将组合数
学、二项展开式系数与三角形阵列这三者联系起来。由于帕斯卡对三
角形的特征进行了详细深入的探讨,因而从此以后人们将三角形阵列
称为帕斯卡三角形。值得指出的是,在论述算术三角形以及点数问题
时,帕斯卡并没有直接使用现代概率学的概念,甚至没有用过概率一
词。相反,他用的是组合数学语言,比如在多次试验中某某事件发生
多少次。因此,后文其实是我用现代化的语言对帕斯卡的研究进行的
重新表述。
帕斯卡三角形以1作为首行开始,接下来各行的每位数字等于上一
行位于它上方两个数字的和。帕斯卡指出,三角形具有许多令人惊讶的特征。例如,如果把首
行称为第0行,那么第n行的数字正是二项展开式(a+b) n的系数。而
第n行左手从0开始第j个数值正好等于n![j!(n-j)!]。
点数问题对概率论的发展至关重要,尤其是运用到机遇游戏(投
资)中。我们回忆一下该问题的基本形式。两人各下一定赌注,谁先赢到n点谁赢得赌注。每得一点都能获得一定奖励,而每轮两人输赢的
概率是一样的。如果当第一个人赢得x
人决定停止比赛,那么此时两人各自应该分得多少赌注?
帕乔利(1494)曾提出,假定两人各下注28个金币,n=6,且两
人的点数为(x,y)=(5,3),此时比赛叫停。帕乔利认为,最公平
的分法就是按照两人所得点数的比例分配金币。在这里,金币总数为
56个,那么第一个人分得35个金币,第二个人分得21个金币。意大利
数学家卡当,亦即有名的罗拉莫·卡达诺(1501年9月24日—1576年9
月21日)曾在1663年出版《论机遇赌博》(Liber de ludo aleae)。
后来亨利·古尔德提出了一个更复杂的解决办法。 [12]他认为应该按
照还没有结束的新比赛的结果来分配赌注。以帕乔利的例子来说,我
们可以设想一个A和B两人的新比赛。如果在B赢得3点之前,A先赢得1
分,则A赢;否则,B赢。那么在这个新游戏中,两人各自对赌注的贡
献是多少?卡当总结说,A投入3×(3+1)=12个金币,B投入1×(1
+1)=2个金币。这样,如果初始赌注为56个金币,那么A应该得到
56×(1214)=48个金币,而B得到56×(214)=8个金币。
帕斯卡三角形
帕斯卡三角形说明了二项树中的再组合问题,在二项树每一个节
点的数字等于上一排两个节点数字之和。更为一般的非再组合二项树
最早由波菲利(大约在公元234—305)推广开来。他是新柏拉图派哲
学 家 , 在 他 的 著 作 《 范 畴 导 论 》 ( Introduction to the
Categories)中用二项树说明了亚里士多德在范畴方面的逻辑论点。
在这个二项树中每一个范畴集合都被分为两个互斥的子集。例如:在帕斯卡三角形中的数字关系的数量开始是无穷尽的。甚至斐波
纳契数列也包含在其中。你是否能发现呢?从左边开始,把一直延伸
到右上角的对角线上的数字相加。那么就有:1=1,1+1=2,1+2=3,1+3+1=5,1+4+3=8,以此类推。
帕乔利和卡达诺的方法都不正确。该问题最终在帕斯卡与费马的
一次著名通信(1654年)中得到解决,此次通信被认为是现代概率论
的发端。他们提出了数学期望的思想并假定每位参与者获得的金币为
倘若比赛尚未结束的情况下他们各自能得到的金币期望值。
费马的方法只需要数数A能获胜的方法或路径个数以及B能获胜的
路径数。在两位选手得分(5,3)情况下,接下来可能的结果为
(a a a)(a b a)(a b b)(b b a)
(a a b)(b a a)(b a b)(b b b)
其中,a表示第一个选手得一分,b表示第二个选手得一分。加粗
的结果意味着第一个选手赢得了比赛。既然在8个可能的结果中有7个
是A赢,那么A就应该得到49个金币,而B得到7个。
帕斯卡提出了另一种类似的解决办法,他使用的是反向递归动态
规划方法。帕斯卡首先问到,如果在双方得分为(5,5)时比赛叫停。由于A
和B两人都有平等的机会赢得56个金币,那么他们每人期望得到的是28
个金币,赌注是平均分配(28,28)。从这儿往后推,如果得分为
(5,4),再比一轮的话,那么一半的可能是(6,4),赌注分配为
(56,0);另一半的可能是(5,5),这种情况已经阐述,赌注分配
为(28,28)。因此,如果得分是(5,4),A得到(12)×56+
(12)×28=42个金币,B得到(12)×0+(12)×28=14个金
币。再往后推一轮到得分为(5,3)的情况,同样的道理可以得到,A
分配(12)×56+(12)×42=49个金币,B得到(12)×0+
(12)×14=7个金币。 2
帕斯卡还被誉为决策论的创始人。在他的《思绪》(Pensées)一
文中 [13],帕斯卡描述了他著名的“赌注”。他对是否相信上帝的分
析十分缜密,让人觉得就应该相信上帝的存在。他说,假设有两种相
互排斥的可能性。第一,如果世上没有上帝,那么相信上帝或者不相信上帝都无关紧要。第二,如果真的有上帝,那么相信上帝会为你带
来永生于天堂的无限幸福,而不信上帝则带来葬身于地狱的无尽痛
苦。这样,即便你主观地认为存在上帝的概率微乎其微,但只要这个
概率大于零,那么你相信上帝所获得的期望收益将会是无穷大。当
然,我们现在知道帕斯卡的推理存在严重的问题,因为他的结果取决
于他对现实世界可能状态的判断。比如,他忽略了另外一种可能,就
是即便存在上帝,信奉者也可能被送进地狱,因为没有人有足够的信
息判断他是否真的相信上帝;而怀疑上帝存在的人,在确定的信息下
拥有正确的观点从而可能上天堂。
尽管帕斯卡成绩显著,但还称不上是第一位决策理论家。在更早
的时候,犹太法典《塔木得9q》(Kethuboth 9q)就提出,男人不能
因为妻子婚前的性行为而与妻子离婚。原因在于,有可能是由于该男
人的关系而使妻子发生了婚前性行为;即便不是前一种情况,妻子也
可能是在并不情愿的情况下发生婚前性行为。总的来说,四种可能情
况中只有一种值得男人与妻子离婚,不值得离婚的情况占了多数,因
而法律上不允许。帕斯卡赌注可能是“施蒂格勒取名法则”的又一例
证。因为在公元303年阿诺庇乌在其著作《反对异教徒》(The Case
against the Pagans)中(第2卷第4章)就描述过类似的选择。
作为现代概率论产生的一个重大特征,帕斯卡也许是不自觉地同
时运用了概率论的二元性:一方面,用概率来解释类似于抛硬币以及
赌博游戏等物理过程。在这类过程中,概率可以无争议地确定(客观
概率),犹如我们在点数问题中所看见的。另一方面,还可以用概率
来解释不可重复事件。在这类事件中,人们对事件发生的概率大小往
往存在较大争议(主观概率),犹如我们在帕斯卡赌注中看见的。因
此,有人如萨维奇(1954)在《统计学基础》一书中就提出,利用本
适合于非重复事件的主观概率使得人们无法在备选方案中做出理性选
择。但是萨维奇的分析只在一种情况下成立,即针对备选方案的打赌
是切实可行的,决定打赌结果的事件是可观测的。比如,我们就人死
之后的结果进行打赌就是有问题的:即便相信死后没有生命的一方获
胜,他也没办法在死后亲自接受赌注。
在20世纪后半叶,数字计算机对投资理论的进一步发展起到至关
重要的作用。不管是利用数据库进行经验验证,还是通过数值分析解
决数学问题,都需要计算机的帮助。我们其实在相当长的时间内使用
了简易计算器,如公元前3000年人们使用的算盘。计算尺大约在
1630~1632年就发明出来。在1642~1644年,为科学做出诸多贡献的帕斯卡当时只有20岁左右,他就成功发明了第一台数字计算机。帕斯卡
的计算机是通过转动转盘来输入数字,通过齿轮来完成加减法。当你
拨动数字时,里面的齿轮就会移动。运算结果显示在键盘上方的窗
口。我们可以在巴黎的法国国立工艺学院看到帕斯卡签名的1652年版
计算机。如果你到伦敦比较方便,那么你可以在南肯辛顿的科学博物
馆看到该计算机的复制品。1657年
克里斯汀·惠更斯(1629年4月14日—1695年7月8日),写了一本
名为《机遇赌博的规律》(De ratiociniis in aleae ludo)
(Calculating in Games of Chance)的小册子,首次以拉丁文形式
出 版 在 1657 年 弗 兰 斯 · 范 · 斯 库 坦 迪 编 写 的 Exercitationum
mathematicarum libri quinque的附录中,随后于1660年以荷兰语出
版在Van rekiningh in spelen van geluck中;后来,雅各·伯努利
(1713)对惠更斯的著作进行了注解;截至2004年3月6日,我们可以
在 互 联 网 上 看 到 该 书 的 英 文 翻 译 版 , 网 址 为
www.stat.ucla.eduhistoryhuygens.pdf。
概率论、期望、套利、状态价格、赌徒破产问题
在1657年之前,惠更斯就已久负盛名,是他发现了土星光环和土
星最大的卫星“泰坦星”(土卫六),是他首次注意到了火星表面的
斑纹。他还在1656年发明了摆钟。紧接着,惠更斯又在1657年出版了
他第一篇有关概率的著作,这是一篇16页的论文,在文中他阐述了期
望的特征。虽说他的论文赫赫有名,但他与帕斯卡(1654)、帕斯卡-
费马(1654)一样,仍然没有使用现代概率的概念。而且,尽管惠更
斯的结果可以用现代概率与期望的概念来解释,但他脑子里有别的想
法。对他而言,期望就是赌博中参与者应该付出的赌资。可以说,是
投资学的某个问题推动了现代概率论的产生(而不是人们猜想的概率
论推动投资学发展),这是思想史上令人称奇的逆向发展之一。
根据伊恩·哈金对惠更斯命题的评论 [14],我们看看如下的抽奖
游戏。游戏参与方有P1和P2两人。由游戏主持方抛掷硬币,由P1来猜
结果。如果P1猜对了,P1将获得X>0的奖金,P2则一无所获。我们将奖
金分配写作(X,0)。如果P1猜错了,P1将一无所获,P2则获得X>0的
奖金,即奖金分配为(0,X)。惠更斯有个隐含假设:参与者交换序
列并不会改变各自得到的奖金。因此,在这个例子中,奖金分配(X,0)的价值应该等于(0,X)的价值。接着,他又提出,如果每个参与
者支付价格(或者赌资)P=X2,那么该游戏是公平的(假设1)。这
跟我们现在所说的套利原理是一致的。设想,如果P>X2,那么游戏主
持方肯定盈利,因为他的总收入大于他提供的奖金:2P>X。而如果
P
损。接着,惠更斯将游戏规则修改了一下,让获胜方同意支付K作为对
输方的安慰奖,0
个人得到的奖金或者为X-K,或者为K,机会均等。惠更斯假定,这一
修改并不改变参与者支付的游戏价格P(假设2)。惠更斯还假定,奖
金分配结果相同的两种抽奖游戏的价格必须是一样的(假设3)——该
假设我们现在称为“单一价格法则”。
惠更斯以三个命题开始:
命题1:如果参与者获得A或B的机会均等,那么他的期望值为
(A+B)2。
命题2:如果参与者获得A、B或C的机会均等,那么他的期望值为
(A+B+C)3。
命题3:如果参与者获得A的机会次数为n 1次,获得B的机会次数为
n 2次,那么他的期望值为(n 1A+n 2B)(n 1+n 2)。
命题1和命题2针对等概率状态。按照现代词汇解释,命题3涉及了
我们现在讲的概率不等情况下的期望概念。我们可以看到比率n 1(n
1+n 2)≡p,于是期望等于pA+(1-p)B。
在300多年后的今天,我们认为命题1理所当然是成立的。可是在
1657年,情况可不是如此。
对惠更斯命题1的证明
假设两个参与者参加一项公平抽奖游戏I,奖金为A+B(A
根据假设1,要使游戏公平,参与游戏的价格必须等于(A+B)2。再
假设,获胜方必须向对方支付一笔安慰奖A。因此,不管哪个参与者,只要他获胜,他就得到(A+B)-A=B;如果他输了,则得到安慰奖A。
可以看出,这个抽奖游戏的奖金分配结果与另一公平游戏II——参与
者有均等机会获得A或B(假设2)——的分配结果是一样的。既然游戏
I和游戏II的分配结果一样,那么他们的价格也必须是一样的(假设
3)。即游戏II的公平价格等于游戏I的公平价格:(A+B)2。命题1
得证。命题2的证明如下:现在有三个参与者P1、P2和P3。既然游戏是公
平的,那么如果P1赢得所有赌资X,他得向P2支付B,向P3支付C。因
此,如果P1赢,他得到A≡X-(B+C)。同样,如果P2赢,他向P1支付
B;如果P3赢,他向P1支付C。这样,P1有均等机会获得A、B或C。P2和
P3也是如此,他们也有均等机会获得A、B或C。表1-1显示了这些结
果: 3
表 1-1
命题3进一步扩展了假设2。惠更斯现在提出一个有n 1+n 2个参与
者的抽奖游戏。每个参与者的赌资为X。游戏是公平的,因为总奖金为
X×(n 1+n 2),每个参与者获胜的机会均等。第一个参与者与其他n
1-1个参与者达成协议,如果他获胜,他将向每个人支付A;相反,如果
是他们中某人赢了,则得向他支付A。对于另外n 2个参与者,他答应赢
了后向他们每人支付B;如果他们中某人赢了,也向他支付B。接着,根据与前两个定理证明类似的道理,他证明了定理3。
令人惊讶的是,惠更斯脑子里的原概念是“价值”而不是“概
率”。把他的定理与现代金融联系起来,仿佛他是直接使用状态价格
π a和π b来思考估值问题(利率近似为零,因此r=1)。其中,出现
π a的概率为n 1(n 1+n 2),出现π b的概率为n 2(n 1+n 2)。
这样,抽奖游戏的价值为π a(A)+π b(B)。
在状态价格的解释中,同样出于套利的原因,状态价格π a和π b
的总和必须为1,而且两者都为正。然而,现代理论并没有接受惠更斯
的隐含假设,即在等概率状态中改变参与者序列并不改变游戏价值。也就是说,在现代理论中,机会均等的奖金分配(X,0)和(0,X)
并不等值。
按照现代观点来看,状态价格不仅反映概率,还反映了风险程度
与风险规避程度。我们知道,惠更斯隐含在假设1背后的观点——参与
者获得X或0机会均等的赌博的价值等于X2——并不一定成立。如果现
实中不存在另外一种奖金为0或X的反向赌博,那么惠更斯的观点就不
成立。根据惠更斯的假设,如果两类赌博都以相同数量存在于同一市
场,那么风险可以完全分散,赌博的价格应该等于期望收益。但如果
只存在一种赌博而另一种不存在,由于风险不能完全分散,赌博的价
格就可能高于或者低于期望价值,是高是低取决于其收益与其他可投
资项目的相关程度、赌博与对参与者而言重要的其他因素的关系以及
参与者的风险规避程度。或者,由于非赌博因素造成参与者的其他财
富在两种状态下不一致,那么这两种赌博的价格也会不一致。比如,如果在第一种状态下参与者的总体财富低于第二种状态,那么即便两
位参与者增加额外赌注,分配结果为(X,0)的价值也将高于(0,X)的价值(当然,根据前文说过的简单套利理论,不管两种赌博的价
格怎样,两者之和肯定等于X)。
突然想到一个现实生活中的例子,2000年爱荷华大学曾办过一次
总统选举赌博,获胜者可以拿走全部赌注。参与者可以出资P B,如果
布什当选总统,他可以赢得1美元;如果布什落选,他得0。参与者还
可以出资P G,如果戈尔当选总统,他可以赢得1美元;如果戈尔落选,他得0。如果我们忽略还有第三位候选人获胜的概率,套利原则要求两
种价格之和P B+P G=1美元。事实上,这只是个极度近似值。我们是
否可以像惠更斯那样将P B理解为布什当选的期望价值,将P G理解为戈
尔当选的期望价值呢?这可不一定。假如参与者预期布什当选总统时
的经济状况好于戈尔,而且参与者们都是风险规避型,那么戈尔当选
所增加的1美元的效用将大于布什当选增加的1美元。或者,参与者赌
布什赢而布什真的当选,那么参与者就无法获得如果他打赌戈尔而且
戈尔当选所能获得的额外1美元,他会因此遗憾。因此,下注布什或者
戈尔的价格不仅取决于主观概率,还取决于效用。最终,赌布什赢的
价格P B将略微低于布什当选的主观概率,而赌戈尔赢的价格P G将略微
高于戈尔当选的主观概率——不管怎样,两者之和都等于1。
利用3个基础命题,惠更斯证明了另外11个命题,提出但未解决5
个问题,其中有些问题是由费马提出来的。定理4至定理9针对的是当时帕斯卡-费马(1654)讨论的点数问题。而定理10至定理14则移至新
的领域。简单地说,命题10回答这样一个问题:一个人需要掷多少次
骰子才会掷出6点?惠更斯利用反向递归的方法解决了这一问题。掷一
次就能掷出6点的概率X 1=16,而不是6点的概率为56。掷两次能得到
6点的概率等于第二次得到6点的概率16加上第二次没有得到但第一次
得到6点的概率(56)X 1。即掷两次得到6点的概率为X 2=16+
(56)X 1。同理,掷三次能得到6点的概率等于第三次得到6点的概率
16加上第三次没有得到但前两次得到的概率(56)X 2。即掷三次得
到6点的概率为X 3=16+(56)X 2。继续推下去,我们可以得到掷k
次得到6点的概率为X k=16+(56)X k-1。根据该公式,我们不难
看出,当k=4时,掷出6点的概率在12至6711296之间[尽管惠更斯没
有解出该数列的公式,我们不难得到X k=1-(56) k]。
最后一个命题,命题14,他把这种递归方法再深入一步,用以分
析比赛轮数没有限制的情况。该定理回答如下问题:假如两位选手轮
流掷两枚骰子。如果A先掷出7点,则A赢;如果B先掷出6点,则B赢;
且由B先掷。问:A获胜的几率为多少?显然,A在第一轮就得到7点的
概率为636,而B在第一轮得到6点的概率为536。惠更斯建立了两个
联立方程。设A获胜的概率为p,那么B获胜的概率最终为1-p。每当B
掷骰子时,情况都和比赛刚开始时一样,A赢的概率都将为p。而每当A
开始掷时,A最终获胜的概率将大于p,假设是q。因此,根据定理3,当B开始掷骰子时,A最终获胜的概率等于:
同理,当A开始掷骰子时,A最终获胜的概率等于:
通过解联立方程,我们可以得到p=3161,即A胜败的概率之比为
31∶30。惠更斯在书中最后附上的5个问题是赌徒破产问题,最初由帕斯卡
提出:两位赌资相同的选手开始比赛。他们将依序进行多轮比赛。每
一轮,第一位选手获胜的概率为p,如果获胜他将从第二位选手的赌资
中拿走1个单位;相应的,第二位选手获胜的概率为1-p,获胜后他从
第一位选手的赌资中也拿走1个单位。一旦某位选手赌资输完,比赛就
结束。问:比赛最多出现n轮的概率是多少?
赌徒破产问题对日后随机游走与布朗运动的发展起了至关重要的
作用。按照现代术语来说,就是在两个吸收壁之间随机游走,其中一
个吸收壁显示第一位选手的得失,另一个吸收壁显示第二位选手的得
失。1713年,哈尔德(2003)在他与皮埃尔·雷蒙德·蒙特莫特的通
信中曾提到尼古拉斯·伯努利解答了这一问题:两位选手赌资不同,能进行多轮比赛。假设选手A的初始赌资为a,B的初始赌资为b;每轮A
赢的概率为p,B赢的概率则为q=1-p。那么,B破产的概率R(a,b;
p)(亦即A赢得所有赌注)的概率为:1662年
约翰·格兰特(1620年4月24日—1674年4月18日)出版了《对死
亡率表的自然与政治观察》(Natural and Political Observations
Made Upon the Bills of Mortality)(伦敦,1662年);再版于B.
本 杰 明 : 《 约 翰 · 格 兰 特 的 〈 观 察 〉 》 ( John
Graunt's‘Observations’),载于《精算学会杂志》,第90卷
(1962),pp.1~60。
统计学、死亡率表、期望寿命
继机遇赌博之后,投资领域首次领略到全新概率推理的好处。反
过来,在投资领域应用概率推理又进一步推动了概率论的发展,统计
学相关领域的发展也由此展开。在这部分的介绍中,我首先得解释人
们如何创建人类死亡率表以及这些表又是如何被用来确定人寿年金的
现值的(人寿年金的支付额取决于年金领取者的剩余寿命)。
进行人口普查的历史至少可以追溯到罗马共和国时期。著名的
《末日审判书》(Doomsday Book)则是多年之后才出现的人口普查清
册,是1086年英国人出于征税目的而编制的。不过,针对该书的数据
类型(其实所有数据类型都可以),格兰特(1662)编写了他第一部
出版的统计分析著作,成为我们知道的第一位统计学家。在当时,格
兰特的分析是独一无二的,就是放到现在他的统计模型亦是令人称奇
的高深。只是那时候人们还不知道用图形来表示时间序列或者横截面
数据,他只能用表格的形式来演示。
依据安德斯·哈尔德(2003)的描述,格兰特的分析是基于每周
搜集的伦敦人口重要统计量数据,数据的起始时间是1604年,某些数
据的时间截至1672年。 [15]和现代优秀的统计学家一样,格兰特因为
担心误差所以调整不合理的峰值,进行一致性检验并寻找支持性证
据。例如,为了计算伦敦的家庭数,他分别依据出生、死亡以及房子
数设计了三种计算方法。然后寻找有效方法来归纳这些数据。例如,他按照死亡原因总结了死亡人数(第2章)见表1-2:
表 1-2格兰特将每年死亡原因中固定的部分(“慢性的”)与变动的部
分(“流行的”)区分开来。他注意到许多居民对某些死亡原因过于
恐惧,因此他希望他的统计数据能让人们放宽心。他还用其他表格列
示了不同死亡原因随时间变化而变化的时间序列数据。尽管格兰特还
不能准确理解样本规模对降低风险的作用,但他已直觉地感受到当他
将样本按时间段(如按时代)进行划分后,趋势会越发明显。利用这
些数据,格兰特率先观测到男性和女性占人口的比率相当接近,而且
长时间稳定不变。他提出并检验了如下假设:在人口死亡相对较多的
年份,新生儿出生较少。
对随后概率论发展最为重要的是,格兰特首次尝试构建死亡率
表。为了制作该表,格兰特必须从数据中推断出总人口的变化以及不
同年龄段的死亡人数。由于他没有直接的相关信息,他想出了一个聪
明的办法,可以依据现有数据推算出来。表1-3就是格兰特最后得到的
死亡率表(哈尔德,2003,p.102):
表 1-3值得指出的是,在17世纪这种分析方法最初被称为“政治算
术”,随后被称为“统计学”。“统计”(statistics)一词的来意
是指搜集并分析与国事相关的事实(status为state的拉丁语)。
1669年克里斯汀·惠更斯和他的弟弟路德维希·惠更斯在格兰特
死亡率表的基础上进行了多项统计创新(这些结果后来出版于克里斯
汀·惠更斯的《拉普拉斯全集》)(Oeuvres Complètes,第6卷,1895年)。路德维希希望通过格兰特表格,根据一个人的目前年龄推
算出他的预期寿命。为了实现这一目的,他假定,在格兰特的观测范
围内,死亡概率的分布是相同的。哈尔德(2003,p.107)用表1-4表
述了路德维希的计算结果。
表1-4 路德维希·惠更斯的死亡率表表中变量x和l x数据直接取自格兰特的表格;d x是l x的一阶方
差;t x是各年龄段起点与终点之间的中点。假定各年龄段的死亡率分
布相同,那么t x就等于那些d x个死亡人数的平均寿命。路德维希推理
到,1822年是100个新生儿生存的总年份数:36个人平均生存3年,24
个平均生存11年,15个平均生存21年。依此类推,所有年份的总和为
1822 年 。 这 样 , 100 个 新 生 儿 在 0 岁 时 预 期 的 寿 命 为 1
822100=18.22=E(t 0)岁。同理,64个人在6岁时的预期寿命为171464=26.78=E(t 6)岁。如果已知某个人现在的年龄,我们用E(t
x)减去x就可以得到他剩余的寿命。克里斯汀当时40岁,路德维希推算
他的剩余寿命在17.5年和15年之间,也就是活,克里斯汀大约还能活
16.5年。
克里斯汀将弟弟的分析更深入一步。他把表格中第一列和第二列
的数字当成一个连续函数,这是最早的分布函数。他演示了如何计算
剩余寿命的中值而不是期望值。他还计算了在两个人A和B中,后去世
的那个人的期望剩余寿命。也就是说,如果T A(一个随机变量)是A的
剩余寿命,T B是B的剩余寿命,他计算的是E[max(T A,T B)]。首
先,对A剩余寿命T A的各个数字,他计算E(T B|T B≥T A)。接着他
对各种可能的期望寿命计算加权平均和,权重为T A的概率。这里我们
看到了条件期望概念的最早运用。如果定义T=max(T A,T B),我们
可以得到生存者的剩余寿命E(T)=E[E(T|T A)],这就是我们现在
说的迭代期望原则。1671年
约翰·德威特(1625年9月24日—1672年8月20日)出版了《人寿
年 金 的 价 值 》 ( Value of Life Annuities in Proportion to
Redeemable Annuities)(1671年用荷兰语出版);另见《保险史与
生命或有理论》(Contributions of the History of Insurance and
the Theory of Life Contingencies),载于《保险杂志》,第2卷
(1852年),pp.232~249。1693年
埃德蒙·哈雷 发表了《对人类死亡率的估计,数据源自布莱斯
勒城的出生与葬礼表,以及对年金价格的探讨》(An Estimate of
the Degrees of the Mortality of Mankind,Drawn from Curious
Tables of the Births and Funerals in the City of Breslaw;
with an Attempt to Ascertain the Price of Annuities upon
Lives),载于《皇家学会哲学汇刊》,第17卷(1693年),pp.596~610。1725年
亚伯拉罕·棣莫弗(1667年5月26日—1754年11月27日) 出版了
《论人寿年金》(A Treatise of Annuities on Lives);再版于棣
莫弗第3版《机遇论》的附加部分《对前版的补充、清晰与修正》;再
版于《美国数学学会学刊》(2000年),pp.261~328。
人寿年金、现值、死亡率表、状态价格、唐提养老保险
现在我们会认为概率论是为投资服务的,可是两者关系并不总是
如此。在早期,是因为我们希望依据死亡率算出现金流的现值,这才
出现了概率的思想。人寿年金是指保险公司每年支付年金领受人固定
金额,直到“被提名人”(通常就是年金领受人)死亡,年金领受人
的本金不偿还。社会保障就是人寿年金的现代大众版。比较常见的是
联合人寿年金,通常用于已婚夫妇或者全体船员,该年金只有在所有
人都存活的情况才继续存在。唐提联合养老保险与它相似,唯一不同
的是只要领受方有一个成员还健在保险金就继续支付。1653年,洛伦
佐·唐提向法国枢机主教马萨林推荐了一个政府集资计划,唐提养老
保险由此得名。唐提养老保险的一般协议是,一组参加保险者向基金
投入相同资金;然后每年他们共同得到一笔指定数额的年金,平均分
配。如果某一成员因为死亡而退出,就由余下成员分享年金总额。由
于年金总额保持不变,因而每人分得的年金增加。当只剩一个成员存
活时,他就得到全部年金。最后当所有参保成员都去世时,年金支付
就停止,基金的本金归基金发行者(如政府)所有。罗伯特·路易斯
·史蒂文森和劳埃德·奥斯本的中篇小说《入错棺材死错人》(The
Wrong Box)(1889)描述了唐提养老保险的另一种形式。参加保险的
初始成员共37人,直到最后只剩一人时该保险才支付保险金额,也就
是说,最后那个人获得全部初始资本与所有累积收益。
在公元前44年恺撒大帝被刺杀到公元前31年阿克提乌姆海战(历
史学家后来称之为罗马共和制灭亡以及罗马帝制开始的时间)的内战
期间,大约是公元前40年罗马颁布了法尔什德法(Roman Falcidian
Law)。根据该法,财产的法定继承人,通常是家中存活的长子,有权
继承该财产至少25%的价值。而非长子则通常是以人寿年金的形式领取
遗产,这样我们就需要知道年金的价值。人们用“收益年份”计量年
金,也就是我们现在说的“回收期”。比如,某笔年金每年支付100
元,收益年份为20年,这就意味着该年金的现行价格为100×20=2000(元)。从3世纪罗马法理学家乌尔比安那里,我们获得一张人寿
年金表。该表格清晰地显示出,年金的价值应该随着领受人年龄的增
长而降低(尽管可能存在人为的上偏,目的是保护长子的财产)。在
他的一份表格中,他指出,当领受人年龄为20时,人寿年金的价值为
30年收益年份;而当领受人的年龄到了60岁,人寿年金的价值只有7个
收益年份。我们现在知道了如何计算收益年份的价值上限。假设生命
是无限的、利息率为6%,那么年金的价值为10.06=16.67(元),即
年金在1个收益年份的价值为16.67。这是年金的最高价值,因为其他
任何事物的价值都低于无限生命的价值。
2000年,杰弗里·波伊特拉斯著书回顾了人寿年金的发展史。 [16]人寿年金始于17世纪,是政府用于集资的途径。年金普遍受到欢迎
的一个原因是它没有违反教会的高利贷法:由于年金购买者只收到利
息,本金并不返回,所以年金并不是债务。当然,年金的二级市场允
许购买者提前套现。那个时候,出现了更为复杂的收益年份概念。假
定P为一笔持续到未来某一固定年份年金的价格,X为年金每年的支付
额,利息率为r。收益年份t满足方程P=X[Σ k=1,2,…,t(1r
k)]。换句话说,收益年份就是让所有年支付额的现值等于年金价格
的时间。
虽然我们看到罗马人已经对年金被提名人的预期寿命进行了调
整,但该调整还比较粗糙。对预期寿命进行精确调整的是德威特
(1671)。在称得上是第一份对期权类衍生品的正式分析中,德威特
提出了一种方法,即基于被提名人的年龄来计算人寿年金的价值。按
照现行标准,他的方法不算精细,但他使用的是当时第一份死亡率
表。德威特假定,被提名人将根据下面的数据死亡。在每768个提名者
中:
在第一个50年中每6个月将有6人死去;
在接下来10年中每6个月将有4人死去;
在接下来10年中每6个月将有3人死去;
在接下来7年中每6个月将有2人死去。
假设复利利率为4%,对768个死亡时间,他一一计算了其对应年金
的现值,然后取算术平均值,即为年金的价格。德威特还指出,他的计算结果可能向下偏,这是因为存在我们现在所说的“逆向选择”问
题:选择购买年金的人可能相对比较健康,因而比同龄人更加长寿。
虽然我们的回顾更注重思想的发展,而不是写思想发明者的传
记。不过我忍不住想提一提,在1672年,也就是德威特出版他有关人
寿年金的经典之作一年之后,他就被荷兰的革命暴徒公开绞死。毫无
疑问,这是因为具有金融天才的德威特在担任政府大臣时太过耀眼。
德威特曾请教过约翰·范·瓦佛兰·郝德(1628年4月23日—1704
年4月15日)。郝德根据1495个实际购买过年金的人的死亡数据,自己
算出了年金价值。哈雷(1693)也设计了自己的计算公式。哈雷使用
了与德威特不同的数据,两人的计算公式却得到了相同的结论。但哈
雷构建了一个更为基础的解答方式。将于时间t终止的年金的现值为
X[Σ k=1,2,…,t(1r k)]。假设qt为年金领受人在第t年死亡的概
率,那么根据德威特的公式,人寿年金的现值为
相反,假设p t为年金领受人在第t年存活的概率。哈雷首先计算e
t≡p tr t,然后再利用这些分子价格计算人寿年金的现值:
证明:哈雷与德威特的公式是等同的
要从德威特的公式推导出哈雷的公式,首先我们要推出年金领受
人在第t年死亡的概率q t与年金领受人在第t年存活的概率p t二者之间
的关系。p t等于领受人在t+1,t+2,t+3…死亡概率之和。如果某人在
第t年还活着,那么他肯定是在随后某一年死亡。因此,在第t年还活
着的概率等于在第t年之后死亡的概率。设想一个具体的例子,年金领
受人在第4年死亡。因此:p 1=q 2+q 3+q 4
p 2=q 3+q 4
p 3=q 4
解上述方程,我们可以得到q 2=p 1-p 2,q 3=p 2-p 3(假设p
4=0,那么q 4=p 3-p 4)。进而,我们得到:
q t=p t-1-p t
该等式的直观意义是:领受人在时间t死亡的概率等于在时间t-1
存活的概率减去在时间t存活的概率。这两个概率产生差异的原因只能
是领受人在时间t死亡。
把上式代进德威特的公式:
将前几项展开看看:
该等式的直观意义是:只有领受人在时间t还活着,他才能在该时
间收到年金,因此时间t期望年金的现值等于p t(1r t)。而各笔年
金之和的现值就等于年金现值之和,这就是该等式的含义。我们可以将e t看成是在第t年你收到1元的现值,条件是当且仅当
你到那时还活着。按照现在人寿年金的说法,这个e t被称为“生存保
险”的价格。保险精算师们将生存保险定义为投保人必须在指定时间
内生存,才能收到的一定款项;如果投保人在特定日期之前死亡,他
生前将什么也得不到。养老保险的条件宽泛一些:不管投保人是否活
过指定日期,投保人都可以收到一笔指定的总数再加上一笔利息。只
不过,如果投保人提前死亡,他得到的收入会有所变化。一般地,在
等额分期支付情况下,如果投保人还健在,他通常会得到补偿。该类
保险可以分解为两部分:一部分是生存保险,一旦在指定日期之前投
保人死亡,该部分就取消;另一部分是投保人提前死亡时支付的条件
保险。
数学家棣莫弗(1725)也研究过人寿年金问题,推导出了单一人
寿年金、联合人寿年金、唐提式养老保险以及退休金等的“解析
解”。他的问题1(pp.265~266)针对单一人寿年金。为了得到解析
解,他假定,生存概率随着年龄的增长而呈等差级数降低:
假定生存概率呈等差级数递减,求某一特定年龄人寿年金的价
值。
根据哈雷的公式,棣莫弗假定p t=1-(tn),这里n可以理解为投
保人剩余寿命的最大值。例如,一位男性现在30岁;如果n=50,那么
他能再活一年的概率为p 1=1-150=0.98;再活两年的概率为p 2=1-
250=0.96;再活50年的概率为p 50=1-5050=0。根据这一假设,年金
的现值为
依据等比级数的特征,棣莫弗指出(式中r ≡r-1):棣莫弗还提供了联合人寿年金的结果(问题2,pp.266~268):
假定已知两笔单项人寿年金的价值,求基于两人联合生存期的年
金的价值。
假设两个年龄分别为x和y的人各自购买了人寿年金,保险合同明
确说明,在两个人有生之年每年向两人各支付1元。设两个人年金的现
值分别为A x≡Σ t( xp tr t),Ay≡Σ t( yp tr t)。再假设两
个人继续存活的概率随着时间而呈几何递减,则 xP t=P t
x, yP t=P
t
y。例如,对年龄为x的人,他再存活一年的概率为p x,存活两年的概
率为p 2
x,依此类推。棣莫弗证明:如果两人为独立个体,那么基于他
们联合生命的年金(即只要两人健在就支付1美元)的现值等于:
我们再具体看看该等式的推导过程。自现在年龄开始,两人再活t
年的概率为(p xp y) t,因而联合年金的现值为A xy=Σ k=1,2,…,∞(p xp yr) t。既然棣莫弗已经提出了这个问题,我们需要按照单
一人寿年金展开该等式。第一人单一人寿年金的现值为A x=Σ k=1,2,…,∞(p xr) t=(p xr)[1-(p xr)]=p x(r-p x)。同
样,第二个人年金的现值为A y=p y(r-p y)。解上述两个等式,再
将p x与p y的表达式代入联合年金A xy的表达式,即得到上述结果。
棣莫弗还考虑了一个唐提式养老保险问题(问题4,p.270):
假定已知两笔单一人寿年金的价值,不管是否谁先死亡,求两人
中较长寿者的年金价值。
无须特别假定 xp t与 yp t不依赖于t,棣莫弗证明了该年金价值
为A x+A y-A xy。很显然,两人中至少有1人在时间t还存活的概率为1-(1- xp t)
(1- yp t)。因此,唐提式养老保险的现值为Σ t[1-(1- xp t)
(1- yp t)]r t。把该式分解为三个部分,一部分为 xp t,一部分
为 yp t,另一部分为 xp typ t,就得到上述结果。
棣莫弗的问题7(p.272)由于“继承”产生的人寿年金的价值:
假设A拥有一笔年金,在A去世后B可以得到一笔人寿年金,求A去
世后B的人寿年金的价值。
同样无须特别假定 xp t与 yp t不依赖于t,棣莫弗证明了该年金
价值为A x-A xy。
同理,很显然,在第t年A已经去世而B存活的概率为(1- xp t)
yp t。因此唐提养老保险的现值为Σ t[(1- xp t) yp t]r t。把
该式分解为两个部分,一部分为 yp t,另一部分为 xp typ t,就得到
上述结果。1738年
丹尼尔·伯努利(1700年2月8日—1782年3月17日) 用拉丁文发
表了《有关衡量风险的新理论说明》(Specimen Theoriae Novae de
Mensura Sortis);后来由L.萨默翻译成英文并出版在《计量经济
学》第22卷,第1期(1954年1月),pp.23~36。1934年
卡尔·门格尔(1902年1月13日—1985年10月5日) 用德文发表
了《论不确定性在经济学中的角色》(Das Unsicherheitsmoment in
der Wertlehre),后由沃尔夫冈·绍尔科普夫在马丁·舒比克所编著
的《纪念奥斯卡·摩根斯顿数理经济学论文集》(Princeton
University Press,1967年)中翻译成英文。
风险规避、圣彼得堡悖论、期望效用、对数效用、分散化、韦伯-
费希纳精神物理学定律、有界效用函数
帕斯卡和费马(1654)在解决点数问题时假定赌博的价格等于它
的期望价值。惠更斯(1657)亦是在该假设基础上形成了完整的机遇
理论。而伯努利的经典之作(1738)则始于这样一个观点:由于风险
规避的存在,赌博的价格低于其期望价值。伯努利用圣彼得堡悖论证
明了风险规避的合理性。如果有机会让你抛掷硬币直到硬币第一次正
面朝上,你愿意为该机会支付多少钱呢?假如在抛掷第n次时硬币首次
正面朝上,你获得2 n美元。该赌博的期望价值为
虽然该赌博的期望价值是无穷大,但你愿意支付的价格肯定只是
有限数目,而且毫无疑问远远低于你的财富总和。因此,赌博的价格
肯定低于其期望价值。
为了解决该问题,伯努利提出每个人都是最大化其期望效用,伯
努利有时称为“道德期望”。伯努利还特别建议使用效用函数
U(W),该函数的特征是“任何幅度的财富增加所产生的效用与之前
持有的财产数量(W)成反比”,即:该方程的解为U(W)=a+b(lnW),或者将效用直接表达为logW的
递增线性表达式。这样的话,赌博的期望效用变为
该等式说明,个人最多愿意为赌博支付4个达克特。伯努利指出,是他的表弟尼古拉斯·伯努利(1687年10月10日—1759年11月29日)
首次提出了圣彼得堡悖论。尼古拉斯原来坚信期望价值是公平本质的
体现,可是悖论的发现打乱了他的信念,这让他非常苦恼。丹尼尔还
指出,早在他之前好几年,数学家加百列·克莱姆在1728年写给尼古
拉斯的一封信中就提出过自己的解法。
早于马科维茨(1952)和罗伊(1952),丹尼尔还提出风险规避
的投资者希望资产分散化:“……应该明智地将各种不同风险的资产
分散开来而不是将他们集中在一起。”第一个意识到分散化好处的人
并不是伯努利。根据犹太法典《塔木德》的建议,“一个人应该以三
种形式保存自己的财富:13存于房地产,另13存于货物,还有13存
于流动资产。”在《威尼斯商人》第一场第一幕,威廉·莎士比亚就
让安东尼说道:……我感谢我的财富。我的买卖的成败并不完全寄托在一艘船
上,更不是依赖某一处地方。我的全部财产,也不会因为这一年的盈
亏而受影响。
虽然《威尼斯商人》后来的剧情说明安东尼的安全措施并不妥
当。但在幕布刚刚拉开时,安东尼对自己的财产非常放心,因为他将
投资分散于不同船只、不同地点以及不同时间。
1851年,恩斯特·海因里希·韦伯(1795年6月24日—1878年1月
26日)在《触觉感官与一般敏感性》(Der Tastsinn und das
Gemeingefühl)一书中应用了伯努利的对数效用。该书成为试验心理
学的奠基之作之一。在该书中,韦伯将人能觉察出的刺激强度的最小
变化定义为“差别感觉阈限”或“最小觉差”。他认为,刺激强度的
变化除以初始刺激强度得到的是一个常数(韦伯定律)。1860年,古
斯塔夫·西奥多·费希纳(1801年4月19日—1887年11月18日)在《心理物理学纲要》(Elemente der Psychophysik)中用该定律解释:虽
然人的大脑和身体看起来是分离的,但它们其实是对同一现实做出不
同的反应。他认为,感觉量(大脑所经历的)的变化与韦伯定律中的
常数成比例。
门格尔指出,凹性效用——就是现在所说的“边际效用递
减”——并不足以解决广义形式的圣彼得堡悖论 4。例如,假设在第n
次投掷中硬币正面首次向上,赌博的奖金是e的2 n次幂。则赌博的期望
对数效用为
门格尔指出,只要效用函数是有限的,圣彼得堡类型的赌博就存
在,其期望效用是无限的。因此,许多经济学家认为,虽然效用有限
仍是个有争议的问题,但有限性是一个合理效用函数存在的前提。
门格尔还分析了解决该悖论的另一个方法,该方法后来被行为经
济学家重拾。即:个人倾向于完全忽略小概率事件产生的结果。该方
法在很早之前由数学家布丰(1707年9月7日—1788年4月16日)于1777
年在《或然算数试验》(Essaid'arithmétique morale)一文中提
出。门格尔指出,人们容易低估极端事件的概率,可能是极小概率事
件也可能是极大概率事件,从而高估中间事件的概率。
门格尔有关无界性的观察使得肯尼思·约瑟夫·阿罗(1965)提
出,不是所有的不确定性结果都满足冯·诺伊曼和摩根斯坦公理
(1947),因为只要效用函数被指定为有界的,或者有上界或者有下
界,那么完整性公理和持续性公理都将被门格尔类型的圣彼得堡悖论
打破。 [17]例如,我们可以想想这样两种赌博,第一个赌博明显优于
第二个,但两个赌博的期望效用都是无限的。不过,这些异想天开的
想法并不能难倒像保罗·安东尼·萨缪尔森这样的人。萨缪尔森
(1977)安慰道:尽管这类赌博吸引了诸多有思想的试验,“但在现
实生活中并不是很重要”。 [18]然而,在不确定经济学的发展过程
中,该悖论的确起了长期的、重大的作用,使得萨缪尔森不得不总结
说:“它在高等知识分子的脑海中拥有崇高的地位”。萨缪尔森提出了一个更令人困扰的拒绝无界效用函数的问题,即
便没有圣彼得堡悖论无限性的存在,该问题仍会出现。假设某人可以
确定得到报酬X(X为金额较大的数值)。如果他的期望效用无上界,那么总会存在一个更大的数Y,使得即便得到的概率很低他也很想得
到。无界效用即是非饱和性的一个极端形式。另一方面,在pp.209~
211中,阿罗(1974)证明:如果效用函数U(X)单调递增,成凹性,U(0)有界,而且E(X)有界,那么E[U(X)]就是有界的。 [19]因
此,如果具有无穷期望价值的圣彼得堡式赌博在现实情况中不存在,那么即便是无上界的效用函数也不会存在问题。1780年
杰里米·边沁(1748年2月15日—1832年6月6日) 出版了《道德
与立法原理导论》(An Introduction to the Principles of Morals
and Legislation)(私人印制);完整版出版于1789年。1906年
维尔弗里多·帕累托(1848年7月15日—1923年8月20日) 出版
了《政治经济学手册》(Manual of Political Economy);由意大利
文翻译成英文,Augustus M.Kelly,1971年。1951年
肯尼思·约瑟夫·阿罗(1921年8月23日—) 发表了《对古典福
利经济学基本定理的拓展》(An Extension of the Basic Theorems
of Classical Welfare Economics),载于《第二届数学统计与概率
伯克利论坛论文集》由J·内曼编辑(University of California
Press,1951年),pp.507~532;再版于《肯尼思·阿罗文集:一般均
衡》第3卷,Harvard University Press,1983年,pp.13~45。
序数效用与基数效用、帕累托最优、竞争均衡的优化
边沁(1780)宣称:人生的目标是追求幸福,而且幸福可以量
化;因此,人们在做决策时,谨慎地计算自己的幸福程度,权衡优势
与劣势。边沁写道:
自然界将人类置于两个主宰者的支配之中:痛苦和快乐。只有苦
乐能指出我们应该做什么以及决定我们去做什么。是非的标准乃至因
果的联系,都由它们定夺。
他还认为,财富是获得幸福的手段(因而从某种程度上说是衡量
幸福的指标之一),但是越来越多的财富带来的幸福增量则是逐渐减
少的——就是我们现在所说的“财富的边际效用递减”(据此他推出
赌博是“不好”的、保险是“好”的)。社会的目标是要让所有社会
成员的幸福最大化,对每个人的幸福值进行平等加权再求和就得到所
有成员的幸福值。把这些想法综合起来就要求进行把财富从富人转向
穷人这样的重新分配,虽然边沁意识到该政策的好处需要与生产率动
力降低的弊端进行权衡。财富再分配的问题之一在于如何确定哪些人
是社会“成员”(只有选民,只有男人,还是只有居民?)。尽管这
些观点后来被现代经济学家几度修改,但“效用函数之父”的称号边
沁当之无愧。
相反,希腊哲学家们则认为,每个人在社会中都扮演着各自的角
色;有些人生来就是奴隶,而另一些人——哲学家们——就应该是统
治者。男人天生就比女人优越。在他们的正义观中,某些人为其他人
谋幸福,或者某些人应该获得比别人更多的幸福,这都是天经地义
的。帕累托(1906)认识到,接受边沁提出的效用基数假设,只需简
单地将偏好解释为序数,也可以得到同样的结论。但更重要的是,他
意识到艾尔弗雷德·马歇尔(1842年7月26日—1924年7月13日)
(1890)的《经济学原理》(Principles of Economics)以及其他人
利用效用进行人与人之间的福利比较太强,因而引出了现在所称
的“帕累托最优”:一种均衡状态,在这种均衡下,不存在另外的资
源分配方式可以在不损害一部分人福利的情况下增加另一部分人的福
利(每个人都用效用评估自己的福利)。后来有人指出,竞争均衡就
是帕累托最优,自此帕累托最优就成为亚当·斯密的“看不见的
手”的强有力支持。
阿罗(1951)也证明了德布勒(1959)描述的竞争均衡的两个优
化定理:
第一优化定理:如果存在均衡,而且所有与偏好和生产相关的资
源都由市场定价,则竞争均衡定是帕累托最优;即消费者之间的资源
配置均衡发生任何变动都不可能在不损害一部分人利益的情况下改善
另一部分人的利益。
这样我们为亚当·斯密(1776)的“看不见的手”找到了现代证
据。
第二优化定理:如果生产规模不存在递增收益且其他某些小条件
得到满足,那么对于资源的初始禀赋分配而言,帕累托最优就是竞争
均衡 5。
第二个定理为判断某个配置是否为帕累托最优提供了一个有效的
方法。假定所有消费者的效用函数为凹性,那么当且仅当该配置在服
从消费总供给约束条件下已经最大化消费者效用的正加权平均之和
时,该配置才是帕累托最优。
帕累托最优是竞争价格体系的现代支持证据之一[其他的支持理
由与激励和信息沟通相关(哈耶克,1945)]:即,竞争价格体系实
现了资源在消费者和企业之间的分配,而且不存在另一种分配方式能
在不损害一部分消费者利益的情况下提高另一部分消费者的利益。第
二个支持理由是,竞争价格体系的均衡存在于“经济的核心”:资源
配置使得每个人至少不差于他的初始禀赋(每个人生来就带着一定的
初始禀赋)。当然,帕累托最优配置组合并不是独一无二的,竞争价格体系只
是挑选其中一个而已。但阿罗指出,通过重新安排消费者的禀赋(在
交换或生产发生之前)竞争价格体系可以实现任何帕累托最优配置。
因此,首先重新分配财富,然后让价格体系自由运转,社会就能实现
它所需要的帕累托最优配置。由于现代经济学家对人与人财富的比较
避而远之,因此,经济学家不会跳出来指出最初的财富分配应该是什
么,那是政治学家的事情。经济学家总是回避最让人头疼的问题。
这些定理由杰勒德·德布勒分别在1951年和1954年的两篇文章中
证明。 [20]1835年
朗伯·阿道夫·雅克·凯特勒(1796年2月22日—1874年2月17
日) 出版了《论人与其能力的发展》(Sur l'homme et le
développement de ses facultés,ou Essai de physique sociale)
(Bachelier,1835年);1942年从法文翻译为英文(Chambers,1942
年)。
普通人或典型人、正态分布、概率在社会科学中的应用
凯特勒(1835)首次提出了“普通人”概念,普通人成为社会科
学领域最著名的虚拟人物。凯特勒根据100000个法国士兵的平均身高
和体重构建了他的普通人。他还更深一步,根据这些士兵的拘捕记录
推出一个普通人的犯罪倾向。普通人的概念在金融经济学发展史上发
挥了重要作用,其影响时间长达一个世纪之久。该概念后来发展为人
们熟知的“典型人”。
凯特勒的第二个重要贡献是,他认为许多自然过程都符合正态曲
线。我的学生卢卡·巴龙告诉我,我们其实应该感谢柏拉图(公元前
427年—公元前347年)。如果我们从更深更广的角度去理解柏拉图的
作品,我们会发现是柏拉图首次描述了单峰对称频率分布,而且他相
信大多数特质都是按这种方式自然地分布的:……因为经验会告诉他事情的真实情况。善良与邪恶都是极少见
的,绝大多数人都是处于这两者之间。我的意思是……你可能想说非
常高与非常矮——非常高与非常矮的人同样是很少见的。这种特征基
本适用于所有的极端情况,不管是大与小、迅速与缓慢、正直与邪
恶,或者黑与白。也不管你是分析人、狗或者任何事物,你都能发现
极端的情况总是极少数,更多的情况是位于中间。见《西方世界的伟
大著作,第1卷:柏拉图篇》(Great Books of the Western World:
Plato , Volume I : Phaedo ) , Franklin Library , 1979 年 ,pp.385~439,尤其是p.415。
凯特勒为正态分布增添了更为具体的特征 6,观察到他的结果有个
重要前提,那就是除了在被考察的差异唯一来源上,样本在其他各个
方面都必须足够同质化。凯特勒对他的正态法则非常自信。因此,当
他观察到身高最低的那个士兵组的人数竟然多于身高较高组的人数时,他就指出,由于服兵役是自愿的,身高最低组的士兵人数较多就
证明了大约有2000人欺骗性地回避了征兵。
1843年,安东尼·奥古斯丁·古诺(1801年8月18日—1877年3月
31日)表达了对将概率论应用于社会科学的严重担忧。 [21]令所有人
都很惊讶的是,在1838年古诺就将数学分析方法引入经济学。他的观
点与他1838年的书一样,都远远领先于那个时代。可是问题出在选择
可验证假说上。古诺认为,社会科学提供了大量挑选与划分数据的方
法,结果造成某些样本看起来支持假说,而且碰巧验证结果在统计上
非常显著。但其实这一结果并不可信。他写道:
很显然,随着我们将样本划分得越来越细,就概率而言,我们就
越有可能得到至少一个小样本其男女出生比率明显不同。
古诺还特别担心人们极易在挑选数据之后再选择假说。现在对这
类错误我们有个名词叫“数据挖掘”。
亨利·托马斯·巴克尔的观点则是另一个极端。他表示:期待有
一天,统计学的力量能融入社会科学,通过数学的运用让社会科学也
能得出像物理学一样精确的预测度。 [22]显然,日后的发展证明,实
际情况介于古诺与巴克尔的观点之间。不过在20世纪中叶,最著名的
科幻小说家艾萨克·阿西莫夫(1920年1月2日—1992年4月6日)在其
小说《基地三部曲》(The Foundation Trilogy)(1951~1953)预
测,大规模应用的社会统计方法将对几百年后的主要社会趋势做出预
测。1900年
路易斯·巴舍利耶(1870年3月11日—1946年4月26日) 发表了
《投机理论》(Théorie de la spéculation)一文,载于《巴黎高等
师范学院科学年鉴》,第17卷,pp.21~86;后由A.詹姆斯·博尼思在
保罗H.库特纳编辑的《股票市场价格的随机游走特征》(The Random
Character of Stock Market Prices)(Risk Publications,2000
年,pp.18~91)一书中翻译成英文;还以法文再版于《投机理论与数
理 游 戏 理 论 》 ( Théorie de la speculation théorie
mathématique de jeu),1995年,pp.21~86。
布朗运动、期权定价、随机游走、正态分布
巴舍利耶(1900)在博士论文中写到,概率论可以用来描述证券
价格的波动。他极可能是有记载以来,进行此类尝试的第一人。巴舍
利耶首次对一个时间连续、状态连续的过程(算术布朗运动)进行了
数学描述,其目的竟是为了对“期权”定价(法语为年金,或者永久
政府债券)。虽然他只部分实现了他的目标,但他的论文——递交给
巴黎科学院的论文——却比爱因斯坦对布朗运动的分析领先了6年,比
布莱克-斯科尔斯公式(基于几何布朗运动)领先了73年之久。
他极有远见地提出现在大家熟知的随机游走与正态分布假设。他
证明了随机性并指出:以当前的价格来看,相信价格上涨的买家人数
与相信价格下跌的卖家人数肯定是一样的。既然我们没有理由判断哪
组人更明智,因此价格接下来向上变化或向下变化的概率是一样的。
于是,他总结到,证券买卖者的期望利润应该是零,证券市场是
个“公平游戏”。
价格随机游走让巴舍利耶发现了我们现在公认的一个结果,那就
是波动幅度与时间区间的平方根成正比 7,而且他还推出了一个描述资
产价格扩散的差分方程。他观察到,如果价格变化是序列独立的而且
在较短时间区间内方差是有限的同分布随机变量,那么根据拉普拉斯
(1749年3月23日—1827年3月5日)(1814)的中心极限定理,较长时
间区间内的价格变动就近似为正态分布。 [23]巴舍利耶还推出了第一
个公开发表的期权定价公式,而且对此进行了经验验证,结果发现市
场价格与他计算的理论价格非常相似。他在论文结尾这样写道:可能最后的备注并不是没有意义的。如果说,在本文讨论的几个
问题方面,我比较了实际观察结果与理论预期结果,这并不能说明结
果证明了根据数学方式建立起来的公式,而只能说明市场不自觉地遵
循着一定的定律,这就是概率定律。
这位金融经济学领域的文森特·凡·高,最终博士论文只得了个
平均分。有意思的是,我们现在将其视为金融经济学领域最杰出的论
文。1906年,巴舍利耶出版了《连续概率理论》(Théorie des
probabilitiés continues)(Gauthier-Villars)。在书中,他定义
了几种随机过程类型,包括随后重新发现的马尔可夫与奥恩斯坦-乌伦
贝克过程。他从漂移与扩散系数角度描述随机过程。尽管巴舍利耶成
绩卓著,可是直到书出版几年后他才找到一份教职。而且从那时开始
一直到1937年他退休,也就是1946年他去世之前9年,他都屈身在一个
毫不起眼的岗位。在很不幸地被人遗忘50多年之后,巴舍利耶的论文
重新被萨缪尔森发现。萨缪尔森在2000年2月8日美国PBS电视节目“新
星2074:30亿赌注”中说道:
在20世纪50年代早期,一个偶然的机会我从巴黎大学图书馆找到
这本不知名的、已经破烂不堪的书。当我翻开它时,感觉就像一个全
新的世界在我面前展开。事实上,我边读就边想一定要将该书翻译成
英文,让大家都来欣赏这熠熠生辉的学术珍珠。 81921年
弗兰克·海尼曼·奈特(1885年11月7日—1972年4月15日) 出
版 了 《 风 险 、 不 确 定 性 与 利 润 》 ( Risk , Uncertainty and
Profit),(Houghton Mifflin),1921年。
风险与不确定性、企业利润来源、投资分散化
奈特(1921)因为两个观点而出名。第一个是他对“风
险”与“不确定性”的区分;第二个是他找到了企业在不确定性条件
下获得经营“利润”的来源。奈特的分析有些让人困扰,很容易让人
用现代的方式误解他的作品。奈特将风险理解为概率可以或多或少进
行客观计量的情况,或者是大数定律能发挥作用通过组合几种可能的
结果进而消除不确定性的情况。
正如我们已经反复重申的,任何一种不确定性,只要它能通过某
种方法简化为一个客观的、可以定量化的概率,那么它就能通过个案
分组简化为完全确定性。(第7章)
而另一方面,奈特将不确定性理解为单一异常事件或者是科学无
法进行清晰预测的事件。一个典型的例子就是在人类事务中人们无法
清晰判断其他人的决策制定能力与决策结果。奈特认为,对于不确定
性事件,我们谈概率是毫无意义的——该观点后来对人们,特别是对
埃尔斯伯格(1961)挑战基于主观形成概率信念的预期效用最大化的
有用性发挥了重大作用。
早在1755年,理查德·坎蒂隆(大约1690年~1734年5月14日)出
版的《商业性质》(Essay of the Nature of Commerce)(实际上写
于18世纪20年代)一书就已经认识到,企业利润来源于企业支付所有
费用(包括利息、工资以及租金)之后企业剩余的报酬。然而,在确
定条件下的竞争性经济体中,所有利润都被竞争化,均衡状态下的利
润为零。于是奈特提出,只有在未来是确定不可知的经济体中,利润
才会增加。如果能获得奈特的许可,我想将他的理论用如下数学公式
(奈特并没有用该公式)加以表达:
r j=r+δ j+ε j (1-14)其中,r j表示企业j的股东已实现的收益,r表示无风险收益,ε j表
示企业已实现收益中能被分散化消耗的部分。现在,我们将ε j称
为“剩余风险”带来的收益。剩下的δ j是奈特将其与不确定性联系起
来的收益部分,也就是奈特所称的“利润”指标。奈特将利润理解为
企业收益中无法被分散化、被套利以及被承保的随机部分。是什么带
来了这部分收益呢?奈特指出,如果概率分布不能被客观地计量,那
么不确定性就不能被分散化。而且最重要的是,人们的决策结果,如
制定企业方针、在企业内选择授权对象,都无法通过概率进行量化预
测。于是,“企业家精神”成为企业利润的最终来源。
能带来利润的唯一“风险”是一种独特的不确定性,他来自一种
终级责任感的实施。该责任感本身无法承保、无法资本化亦无法薪酬
化。利润源自事情固有的、绝对的不可预测性,源自一个坚定的事
实,那就是人类活动的结果无法被预期,就它们进行概率计算是根本
不可能的,也是毫无意义的。(第10章)
δ j的期望价值是多少呢?对奈特而言,由于我们现在所说的如下
行为因素的原因,市场最好预测E(δ j)<0。第一,企业家可能过度
自信进而过度投资;第二,因为不能理解所谓的“赢家诅咒”而过度
支付;第三,一旦已经投入资本就不愿意放弃计划;第四,为自己工
作的满足感。不过,奈特的脑中显然没有我们现在称为“系统风
险”的概念。系统风险是指整个社会都面临的风险,每一个个体都无
法逃脱,无法不因此牺牲期望收益的风险。1923年
约翰·梅纳德·凯恩斯(1883年6月5日—1946年4月21日) 发表
了 《 论 商 品 市 场 的 某 些 问 题 》 ( Some Aspects of Commodity
Markets),载于《曼彻斯特卫报》,1923年。1949年
霍尔布鲁克·沃金(1895年—1985年10月5日) 发表了《存储价
格理论》(The Theory of Price of Storage),载于《美国经济评
论》第39卷,第6期(1949年12月),pp.1254~1262。
即期价格与远期价格、远期价格与期望价格、正常逆价、便利收
益、套利与投机
金融经济学吸引经济学家最早的问题之一便是期货交割的今日价
格(期货价格或远期价格F 0)与未来标的资产在交割日的期望价格
E(S t)的正常关系。凯恩斯(1923)在一篇刊登在报纸上的文章中首
次提出了期货市场的“正常逆价”(normal backwardation)理论
(也称现货溢价或期货折价理论)。他指出,F 0通常低于S t的预期价
值。他认为,通常做空的套利者为了让投资者接受风险不得不向他们
支付一定风险溢价。凯恩斯(1930)更详细地阐述了这个观点。 [24]
当然,我们不难理解,对于某些类型的标的资产,套利逻辑(对
此我会进行更新并加入风险规避)会产生正常逆价现象。例如,如果
标的资产是某股票市场指数,假定没有套利且市场完备,则F 0=S
0(rd) t,其中S 0为标的资产的当期价格,r为无风险收益率,d是
指数的回报率,t是交割期。通常,由于风险规避意味着E(S t)>S
0(rd) t,因而我们得到F 0
用于消费或生产目的的标的资产(也就是商品)非常有意思。对
这些资产,由于标的商品不能轻易卖空(借用或者出售),套利无法
使得F 0=S 0(rc) t,其中,c等于1加上存储成本率;它只能保证S
0c t≤F 0≤S 0(rc) t。对于E(S t)
样的情况。因此,在考虑持有标的商品的机会成本之后,商品的远期
价格是否会低于其预期即期价格就是个非常有趣的问题。用公式表达
为:F 0< E(S t)(rc) t。这为商品的当期所有者带来的额外收
益,该收益被尼古拉斯·卡尔多(1939)称为“便利收益”。 [25]
正如约翰R.希克斯(1904年4月8日—1989年5月20日)(1939)所
言,投资者通常不得不被劝诱购买商品期货,因为他们本来不喜欢这种状态。 [26]
他们知道,已经提前安排好的某一特定日期的需求与供给(通过
远期合约)与那天真正到来时的供需没有什么关系;尤其是,他们根
本无法提前准确说出在未来时期他们自己到底愿意买多少或者卖多
少。因此,一个正常生意人愿意签订远期合约的原因只能是这样做他
能“套利”——也就是说远期交易能降低他现在面临的风险。而且只
有在他以某种方式承诺进行销售或购买行为时这种情况才会发生……
技术环境使得企业家控制投入要素的获取比控制产出的完成更加自
如。投入要素大多是用于开始新的流程;而产出的生产流程……可能
已经开始。因此,虽然有些人期望能固定一个未来买入计划,但更多
时候人们更希望固定一个未来出售计划。(第2版,p.137)
凯恩斯和希克斯认为,在选择什么时候、是否购买以及向谁购买
生产投入要素方面时,商人通常具有较多弹性(现在我们称他们拥有
更有价值的“实物期权”)。而当商人不得不销售由他们部分或者完
全负责的产出时,则弹性较小。按照凯恩斯和希克斯的说法,商品的
需求方存在“先天劣势”。弥补远期交易需求疲软的是投机者,他们
缺乏做多的自然理由。为了让投机者做多而且承担风险,必须付给投
机者一定的便利收益(即更低的远期价格)。
由于无法观测到预期的未来即期价格,正常逆价的特征就是随着
交割日的临近,远期价格逐渐上升(高于持有商品的机会成本)。
通常人们认为,期货的今日价格大部分取决于人们今日对期货在
未来交割日的即期价格的预期。而且,由于交割日不同带来的相同期
货的价格差异反映了人们对不同日期即期价格的预期差异。沃金
(1949年12月)指出,这并不总是正确的。
沃金指出,即便商品的即期价格发生变化,或者预期收成发生变
化,时间t(比如2006年1月)市场报出的将于时间t+k(比如2006年9
月)交割的商品的期货价格与时间t+h(比如2006年3月)相同商品的
价格之比是稳定的。沃金提出,这个观点成立的一个重要条件是商品
的当期库存相对于预期未来库存较为充沛,因此我们可以存储商品至
远期交易。因而,商品的当期价格可以进行调整使得商品持有人只要
能弥补他将商品留作存货的存储成本,那么他不管是在时间t、t+h,还是t+k售出商品都是无差异的。由于商品存储时间越长,存储成本就越高,因而在更远期交割的期货价格比在近期交割的期货价格要高,差异产生的原因就在于存储成本。
但有的时候期货价格会发生倒转,导致近期期货价格高于远期期
货价格。一旦相对于未来需求而言当期库存较低或者未来收成预期较
大时,这种情况就会发生。这时,我们不应该将任何当期存货持有到
远期,所有存货都应该在下次收成之前全部消耗掉。这使得期货价格
不再受存储成本的影响,并带来“便利收益”。1930年
欧文·费雪(1867年2月27日—1947年4月29日) 出版了《利息
理论》(The Theory of Interest:As Determined by Impacting to
Spend Impatience and Opportunity to Invest It),Macmillan,1930年。
跨期消费、生产、汇率、利率、费雪效应、急躁与机会、费雪分
离定理、竞争性市场、一致同意与帕累托最优、实物期权、投机、资
本预算
费雪(1930)是20世纪大多数投资金融理论的奠基之作。费雪完
善并重述了早前出现在费雪(1896)、费雪(1906)和费雪(1907)
中的许多研究成果。 [27]费雪指出,他的部分思想受到约翰·雷
(1796年6月1日—1872年7月12日)1834年论文的启发, [28]为此,费
雪还将其1930年的著作献给雷。费雪创建了第一个正式的、描述既有
跨期交易又有生产的经济系统的均衡模型。在这个过程中,他一下子
就推出计算财富的自然经济结果就是计算现值,他还证实生产的目的
是为了使现值最大化。另外,他还分析出了用于计算现值的利率的影
响因素。
费雪假定,每一个市场参与者都同时是某一大类消费商品的消费
者与生产者。单一商品的简化使他能从多商品瓦尔拉斯范式下不必要
的纷繁复杂中进行抽象提炼。而且自那以后单一商品的假定成为金融
理论研究的核心。每个交易日,交易受到一笔期末到期、无违约风险
的短期债券的收入的影响。在该分析框架下,费雪对经济思想史的贡
献在于:①分析了实际利率的影响因素以及总消费的均衡跨期路径;
②提出“费雪效应”,分析了名义利率与实际利率以及通货膨胀率之
间的关系;③提出费雪分离定理,指出应该将生产决策授权给以现值
最大化为目标的企业,而不需要直接依赖股东偏好;企业的融资与生
产决策应该分离开来。投资金融理论的大多数后续工作都可以看成是
对费雪观点的进一步完善,尤其是在分析中加入了对不确定性的考虑
以及使用更为复杂的金融工具用以分析消费跨时间与跨地区的分配。
费雪将现有两种解释利率的观点协调起来。一种观点从产出效率
(“机会”)出发,另一种则是基于消费心理学或时间偏好——或
称“急躁”。“急躁”一词是由费雪(1907)在《论利率》一书中创造出来的,用以提出一个综合性理论:“因而,利率的存在是因为人
们总想尽早消费,一刻也不耽误;而如果让你推迟消费,那么你的未
来收入就要增加,这增加的部分就是利率”(p.495)。
费雪通过文字、图表以及公式三种方式来描述他的经济系统。有
意思的是,即便经济思想史发展到此时,费雪发现使用代数公式仍是
非常有用的。他指出,使用公式可以让人很清楚地知道,待求变量的
个数与独立方程的个数是一样的。另外,他还写道:
认为用数学公式描述经济问题只是展示了一个不符合实际情况的
理论精确模型的观点是完全正确的。但是,在我看来,这绝对不是一
个缺点,而恰好是个优点。因为我们可以根据数学公式清楚地指出哪
些地方是不符合实际情况的。(p.315) 9
费雪设计了一个只有2个时间段3个消费者的简单例子。在这个例
子中,只有消费者的时间偏好影响利率。设:
r为均衡无风险收益率;
为第i个消费者在时间0和时间1的初始消费金额;
x i
0,x i
1为第i个消费者在时间0和时间1选择的借款或放贷金
额,消费者的预算约束为 x i
0+x i
1r=0;
[29]是第i个消费者
在时间0和时间1选择的最优消费金额。
接着,他假设消费者的时间偏好率取决于他选择的消费流:f i=F
i(C i
0,C i
1)是消费者i的时间偏好率。
在第12章的附录中,费雪将时间偏好率与消费效用U i(C i
0,C
i
1)联系起来:f i=[U′ i(C i
0)U′ i(C i
1)]-1 (1-15)
他提出,在均衡状态下,每个消费者的时间偏好率都必须等于无
风险收益率,即:
f 1=f 2=f 3=r (1-16)
为了让市场出清,他要求在每个时间所有消费者的净借款与贷款
额为零:x 1
0+x 2
0+x 3
0=0,x 1
1+x 2
1+x 3
1=0。这样,一共有7个未知
数:C 1
0、C 2
0、C 3
0、C 1
1、C 2
1、C 3
1以及r,相应有7个独立方程。
费雪的经济系统
设:
U(C 0),U(C 1)为时间0和1的消费效用;
ρ为急躁率;
Ω 0为消费品的初始禀赋;
X 0为Ω 0已经用于生产的部分,这样C 0=Ω 0-X 0;
f(X 0)为时间1消费品被用于生产而得到的产出,这样C 1=f(X
0);
W 0为消费者的现有财富,因而W 0=C 0+C 1r。
假设U′(C)>0(非饱和),U′′(C)<0(边际效用递减),0<ρ<1(更偏好当期消费而不是未来消费),f′(X 0)>0(投入增加
产出增加),以及f′′(X 0)<0(规模收益递减)。
消费者的生产问题为,约束于C 0=Ω 0-X 0以及
C 1=f(X 0)
代入约束条件,对效用函数求微分,并让导数等于零以得到最大
值,则得到:
消费者的交易问题为:
,约束于W 0=C 0+ C 1r
同样,代入约束条件,对效用函数求微分,并让导数等于零,便
得到:
把上面两个结果联系在一起,就得到:
这样,我们就得到利率的双边决定因素:均衡无风险利率等于我
们现在说的边际替代率(费雪称为“时间偏好率”),也等于资本的
边际产出效率。再举个更具体的例子,设U(C t)=lnC t,f(X 0)=αX β0,其
中0<β<1且α>0。这满足效用函数与生产函数的求导条件。α可以解
释为产出效率的纯指标,因为α越大,一定投入带来的产出就越多。
代入方程(1):
解未知数C 0和r,得到:
C 0= ( 1+ρβ ) -1Ω 0 , 且
对无风险收益率公式求导:
于是我们看到了费雪提出的急躁率(ρ)与机会(α)对利率的
完全独立影响。
费雪还指出,不同时间段的独立利率是经济力量的自然结果,在
完备市场中是无法通过套利消除的。
另一个推论就是,我们有必要为每个不同的时间段设定一个独立
的利息率。用更务实的话来说,我们需要认识到短期利率与长期利率
的差异。该差异不像博姆-巴韦克想的那样是因为市场不完备引起的因而可以消除。这些差异之所以产生是因为企业收入流的构成存在无穷
尽的变化。任何单纯的价格套利都无法消除这些差异。(p.313) 10
费雪总结到:利率受到以下因素的影响:①不同时间资源禀赋的
相对分布;②消费者与投资者的时间偏好;③将当期总禀赋转化为未
来总消费的生产机会;④资源禀赋的一般规模;⑤风险规避与风险的
时间结构;⑥预期的通货膨胀率。费雪将因素②产生的原因归结为缺
乏远见、无法自我控制、习惯形成、预期寿命以及遗赠动因,这显然
是一种行为导向的解释。他说明了所有这6个因素如何影响经济参与者
的决策以及这些决策又是如何最终影响均衡利率的。
接着,费雪分析了他的理论可能受到的批判。其中一个大家常质
疑的就是将利率的影响因素与跨期消费选择的特征联系在一起可能是
个不错的想法,但这样做太狭隘。事实上,利率主要是由“可贷资金
的供需关系”决定的。费雪回复到,资金的供需只是更为基本的生产
者现值最大化的需求以及消费者最优化平衡人生各期消费的需求的中
间效应。不过,他也承认,可能还有些他尚未涉及的复杂的制度因素
会影响利率,但那些因素的影响是次要的。
费雪将他的分离结果表述如下:
但我们看见,在我们所假设的一个充满选择的世界中,资本家通
过结合两类收入选择实现了其最终收益。在我们的假设中,这两种收
入选择是完全独立的。再重述一次,这两类选择是:第一,从各种可
能的收入流中选择具有最高现值的收入流;第二,通过借贷或者买卖
选择该收入流各种可能的修正方式。第一个选择是在具有不同市场价
值的收入流之间进行选择;第二个是在具有相同市场价值的收入流之
间进行选择。(p.141) 11
必须谨慎解释这种“分离”,它并不意味着第二个选择完全独立
于第一个选择。要弄清楚第二个选择到底是什么,我们首先得知道第
一个选择的含义。不过,可以在做出第二个选择之前做出第一个选
择。费雪还清晰地指出,他的分离结果取决于一个竞争性市场,在这
个市场中,资本家自身并没有意识到他们可能对利率造成影响。另
外,费雪指出,他的结果需要假定借款利率和贷款利率是一致的(市
场完备)。这表明,企业的行为是追求现值最大化。在不知道股东的偏好和
禀赋的情况下,企业制定的生产决策与它们的股东是一致的。如果的
确如此,那么这可以大大简化竞争经济中的资源配置问题。
对费雪分离定理的证明
为了推导分离定理,继续我们之前的例子。假定将生产决策委派
给一个追求现值最大化的企业。这样的企业将选择X 0来使:
其中不考虑可能多r产生的影响(即选择X 0时,dX 0dr=0)。对
现值进行微分并将之等于0。那么r=f′(X 0),这与代表性的消费者
自己制定决策的结果完全一样。
尽管如此,马克·鲁宾斯坦1978年提出,费雪分离定理(在完备
与竞争性的金融市场中,以现值最大化为目标的企业所做出的投资决
策是全体股东都一致同意的)基本上是错误的,在一个投资者充分分
散化的市场尤其如此,这是因为竞争假说并不稳健。 [30]
有时,完全竞争被定义为要求任何一家企业的行为都无法影响价
格。1934年,琼·维奥莉特·罗宾逊(1903年10月31日—1983年8月5
日)针对边际生产成本递增的商品对该要求的实际合理性提出了质疑
(如果在所有企业都以相同价格销售相同商品的市场中,不止一个企
业生存下来,那么边际生产成本就是递增的)。因为此时,企业数目
必须是无穷多的。在企业数目有限的情况下,一家企业增加产出,其
他企业的最优产出就相应降低。其他企业产出的降低会部分但不会完
全抵消那一企业产出的增加,从而使得商品价格发生一定程度的变
化。 [31]她总结道:
如果我们都承认如下情况为完全竞争:一家企业增加一单位产出
所造成的价格下降幅度小于某个特定的有限数额。那么,不管边际成
本曲线的斜率如何,都存在一定数量的企业使得市场实现完全竞争。
边际成本曲线的斜率越小,企业数目就越少;边际成本曲线的斜率越
大,企业数目就越多。(p.119) 12如果根据罗宾逊的经典论文来定义竞争,那么全体股东一致同意
的情况就基本上不会发生(凭经验,发生的概率极低)。我们只需要
用一个确定状态下的单一时期经济体就可以说明。其基本思想在于当
市场上存在大量小企业,每一个企业的生产决策对利率的影响都微乎
其微(效应1),同时充分分散化的投资者也只将自身财富的一小部分
投入单家企业。因此,单家企业对投资者财富的影响也是微乎其微的
(效应2)。这样,在为企业生产决策投票时,每个投资者都需要在这
两个效应之间进行权衡。由于一部分投资者(贷方)希望利率较高而
另一部分投资者(借方)希望利率较低,他们会意见不一。罗宾逊在
论文中指出,增加企业数目并不能解决这一问题,其结果只能是导致
两种效应都同比例降低。
虽然基于现值计算做出的决策通常并不能得到所有投资者的一致
同意(除非他们是完全相同的),但仍是帕累托最优。他在论文中指
出,现值最大化的最大好处在于,不管企业股东是谁,企业都能根据
该方法做出帕累托最优投资决策,而且是唯一的方法。尽管该论文在
20多年前已经出版,基础性金融学教材仍然一致同意在这个错误假设
基础上推出现值最大化的合理性。其中一本著名的教材仍将“一致同
意”列为金融经济学的七个伟大思想之一。
费雪可能是首位强调我们现在所说的“实物期权”对提高柔性生
产机会作用的经济学家。柔性生产机会对如今企业投资的现值计算起
着重要的作用。
这为我们带来了大量重要的选择类别;即我们可以选择更新或修
理设备,还可以选择进行不同程度的更新与修理……但是,除了选择
保留稳定数量的商品库存外,企业主还有许多其他选择。他可以选择
以赚取利润的速度扩大企业规模……第三个选择是逐渐关闭生意……
另一类收入流选择常见于对不同生产方式的选择,尤其是对不同程度
的所有资本主义生产方式的选择……企业家们面临的这些备选方案通
常可以划分为短期决策和长期决策。短期决策涉及一些构造简单、易
消耗的设备;而长期决策涉及生产成本巨大、但极为耐用的设备。……在上述所有情况中,只要企业选择能使未来收入流现值最大化的
设备更新、修理或者改良决策,企业就能得到“最优”结果。
(pp.194~199) 13
费雪还分析了利率变动的动态特征。例如,利率的变化可能改变
人们对生产机会的利用,而这又反过来稳定了利率,造成我们现在看到的均值回归现象。
尽管费雪对不确定性的一阶效应进行了定量分析,但他同时也表
示,要对理论进行正式归纳不容乐观:
试图用数学公式有效且全面地描述随机波动的利率的决定机制,就如同试图准确描绘在风力作用下导弹的轨迹一样。这样的数学公式
要么得具有高度的总括性,要么完全是经验式的,否则都会失去价
值。(p.316) 14
于是,费雪把大量经济现象都留给他人来解释,如同时使用保
险、债务和权益,对流动性的需求,投资组合分散化,具有不同收益
证券类型的高度多样化,所有这些现象的存在都依赖于不确定性。
费雪在1906年出版的《资本与收入的性质》中阐述了他对市场理
性以及投机作用的观点。
当人们投资公开发行的证券时,通常会出现一种现象,即人们往
往不是独立地对证券价格进行预测。此时,投机的结果就会尤为不
幸。出现危机、恐慌、银行挤兑等事件的主要原因就是人们不是独立
进行风险估计,而是相互模仿。……而另一方面,只有当投机是基于
独立知识时,投机的效用才是最大的。投机者的专业知识可以降低风
险,而且还可以让风险从缺乏知识的人身上转移到拥有知识的人身
上。……风险是最可怕的经济罪恶之一,所有有助于消除风险的方法
——不管是保证、安全保护、远见、保险或是合法投机——都能为人
类造福。(pp.296~300)
1958年,杰克·赫希雷佛将企业的资本预算理论整合进费雪的同
期消费与投资选择模型。他设定了一个较强的经济基础,解决了许多
有关现值使用以及将内部收益率作为投资标准的争端。而且,他还分
析了一些市场不完备现象如借贷利率差异的影响,分析了资本预算以
及相互排斥投资项目的选择。 [32]1931年
哈罗德·霍特林(1895年9月29日—1973年12月26日) 发表了
《 可 耗 竭 资 源 经 济 学 》 ( The Economics of Exhaustible
Resources),载于《政治经济学》第39卷,第2期(1931年4月),pp.137~175。
可耗竭资源、霍特林法则、视为期权的矿产开采、黄金
假定(按照我们现在的说法)没有套利、市场完备且充分竞争、没有不确定性,霍特林(1931)得到这样一个结论:可耗竭资源(如
稀有金属、铜、石油等)的价格必然以无风险利率的速度增长。这通
常被称为“霍特林法则”。我们假定P 0为每单位资源今天的价格,每
年的无风险利率为r,那么在t>0年之后,每单位资源的价格将变为P
t=P 0r t。他的理由如下,在竞争均衡状态下,资源的开采速度应该保
持在这样一个水平:在两个时期之间转移开采不再带来任何边际收
益。这样,不管资源拥有者决定在今天还是在今后某天(t>0)开采并
销售资源,他拥有资源的现值都是一样的。但是如果这是真的话,那
么未贴现的价格就必须以无风险利率的速度增长,即如果P 0=PV 0(P
t),则P t=P 0r t。由于存在开采成本,该法则的含义应该修改为扣
除开采成本之后的价格应该以r-1的速度增长。接着,霍特林指出,人
们对可耗竭资源会迅速耗竭的普遍担忧是没有必要的。只要资源行业
是竞争性的,资源就会以社会最优的速度进行开采,而且无需政府干
预。
霍特林自己没有将法则推广到不确定的情况,而是将工作留给了
他人。在这里,我们有必要区分两种不确定性:①供给不确定,原因
可能来自开采成本、矿容量或者勘探速度;②需求不确定(即使用资
源的未来价值)。金融经济学家对后者尤其感兴趣。比如,假设有一
口油井,我们知道它的容量和开采成本,那么它的开采速度应该是多
少?奥克塔维奥A.图里奥(1979)首次把这个问题当做期权来进行分
析。 [33]他比较了两种选择,一是选择开采资源,一是选择执行一个
永久保护性的美式看涨期权,标的是成交价已知且固定的石油价格
(比如开采成本)。正如一个人绝不会优先提前执行这样一个看涨期
权一样(萨缪尔森-默顿,1969),这个人应该同样不会开采石油。然
而,与之相矛盾的是,现实生活中人们仍然在开发石油。图里奥的回答是,因为开采成本以足够快的速度增长,使得开采达到最优水平。
然而,如果开采成本是固定的,图里奥就仍没解开这个谜团。很显
然,即便开采成本已知而且是固定的,经济系统也不会选择永不消费
石油。虽然之后的分析大部分解决了有关用于消费的可耗竭资源的这
个谜团,但对于像黄金这样主要用于投资而不是消费目的的资源,这
个问题仍悬而未决。即便我们不用担心私人金矿会被国家征收,这个
问题还是存在的。
1990年,迈克·约翰·布伦南在美国金融学会主席致辞中分析了
如下问题:如果黄金主要是用于投资目的,开采成本的增长速度又慢
于利率,而且金矿不会被国家征收,那么金矿所有者为什么要开采黄
金呢?这个开采黄金的机会就类似于一个永久性美式开涨期权,人们
不会提前执行。然而,布伦南观察到,企业仍然在开采。他认为,这
是因为如果要让公司股票有个合理估值,企业需要开采黄金向投资者
证明他们确实拥有他们宣称的黄金储备量。 [34]然而,布伦南的解释
给我的感觉则是难以令人信服。不过,就像夏洛克·福尔摩斯所说
的,一旦我们分析并拒绝了可能的解释,不管剩下的是多么不可能,都肯定是真的。1933年
阿尔弗雷德·考尔斯三世(1891年9月15日—1984年12月28日)
发表了《股票市场预测师真具有预测能力吗?》(Can Stock Market
Forecasters Forecast?),载于《计量经济学》第1卷,第3期
(1933年7月),pp.309~324。
投资业绩、有效市场
考尔斯(1933)可能是第一本公开出版的对专家“战胜市场”能
力进行统计检验的著作。考尔斯分析了1928~1932年期间16家金融机构
对个股的7500个推荐意见。他对样本进行了如下特征描述:
预测者包括各个代表性领域的知名机构,它们大部分都规模庞
大、资金充裕,聘用能力非凡的经济学家和统计学家。……一些预测
者看起来似乎得到了德尔斐神谕的指示,用一些模棱两可的语言来表
达他们的预测。(p.309) 15
依据推荐意见得到的年投资收益比市场平均收益低1.4%。考尔斯
比较了实际预测者的收益分布与由随机挑选股票组成的投资组合收益
的分布,他发现,还是没有显著的统计证据表明预测者的能力强过市
场。他还考察了20家顶级火险公司的投资与24份金融出版物的预测,仍没有找到能够战胜市场的证据。而且,那些最失败的投资者似乎比
随机投资的业绩还要差。
1968年,J.G.克拉格和伯顿G.马尔基尔提供了一份与考尔斯类似
的最新研究。他们着重考察了证券分析师预测公司未来盈利的准确
度。令他们惊讶的是,他们发现分析师的预测并不比我们根据过去的
盈利增长进行简单推算来得更准确。 [35]1934年
本杰明·格雷厄姆(1894年5月8日—1976年9月21日)和戴维L.多
德 出版了《证券分析:原理与技术》(Security Analysis:
Principles and Technique)(McGraw-Hill,1934年);多次修改
后,作者包括杰明·格雷厄姆、戴维L.多德和西德尼·考特勒
(McGraw-Hill,第4版,1962年)。1949年
本杰明·格雷厄姆出版了《聪明的投资者》(The Intelligent
Investor),第4版(HarperCollins,1973年),首次出版于1949
年。
证券分析、基本面分析、资本结构、增长与价值、再平衡、定投
法、有效市场、数理金融、投资业绩的极端值
在最为著名的有关股票市场的著作中,格雷厄姆和多德(1934)
宣称,考察投资价值以及设计投资技巧的最基本方法是分析资产负债
表和损益表。从随后的研究发展来看,他们的主要不足在于:①没有
充分考虑投资分散化的作用;②没有考虑风险在均衡状态下对价值决
定的影响;③没有充分考虑促使市场信息有效的因素。
格雷厄姆和多德对企业资本结构相关性问题的探讨很有启发性。
他们比较了3家企业,它们每年的经营现金流相同(都是1000000美
元),但资本结构不同,可参见表1-5。
表 1-5 (单位:美元)
假设债券的利率为5%,股票价值与股票收益比率为10∶1。这样,对企业B,股票收益=1000000-(0.05×5000000)=750000;对企业
C,股票收益=1000000-(0.05×10000000)=500000。依据10∶1的资
本化率,企业B的股票价值=750000×10=7500000;企业C的股票价值
为=500000×10=5000000(pp.461~463,原始版,1934)。他们立即发现,这个情况是他们始料未及的,因为具有相同现金
流的3家企业居然总价值不同。这个表格告诉我们,企业一旦改变资本
结构,企业价值就会受到影响。这引发他们提出一个问题:“资本结
构的随意变动是否能改变企业价值?”在更详细考察之后,格雷厄姆
和多德指出,企业A的股票其实可以解释为企业B的债券与股票的组
合 。 因 此 , 理 论 上 , 企 业 A 的 股 票 价 值 应 该 为 =
5000000+10×(1000000-0.05×5000000)=12500000。这与莫迪格利
安尼-米勒(1958)和莫迪格利安尼-米勒(1969)的分析已经极为接
近。此时格雷厄姆和多德距离投资史上最为重要的思想之一仅有一步
之遥。遗憾的是,他们紧接下来的分析却偏离了前途光明的大道:
但是在现实生活中,企业A的12500000的股票价值通常无法被实
现。显而易见的理由是,普通股的购买者不会意识到普通股发行中存
在“债券组成部分”;而且在任何情况下,投资者都不希望出现这个
债券构成,因而不愿意为此进行额外支付。这个事实告诉了证券购买
者以及企业管理层一个重要原则,那就是:
企业最适宜的资本结构中,高级证券的组成部分应该是可以安全
发行并用于投资购买的证券。(p.463)
格雷厄姆(1949)在其投资经典之作《聪明的投资者》中有力地
阐述了他的投资哲学。被称为“价值投资之父”的格雷厄姆建议人
们:应该在仔细分析企业基本面的基础上进行投资,要密切关注市盈
率(PE)、股息率以及证券分析中使用的其他工具,只投资于那些股
票市场价值尚未偏高于企业有形资产价值的股票。虽然有些成长型股
票事后显示收益率很高,但格雷厄姆认为,这些股票的价格可能发生
不可预测的极端波动,投资的风险太大,不值得推荐。他的基本原则
是将可投资财富在高等级债券与由10~30只股票组成的投资组合之间进
行划分,保持两类投资占总财富的比例至少为25%。然后定期进行调整
实现预定的目标比例。他还推荐定投法,即投资者定期投入相同金额
购买普通股,而不是一次性投入。他认为“按照这种方法,当市场下 ......
您现在查看是摘要介绍页, 详见PDF附件(8389KB,491页)。