杜文久 周 娟 李洪波

    (1西南大学数学与统计学院,重庆 400715)(2重庆市教育考试院,重庆 401147)

    1 引言

    教育和心理测验都是由相应的测验项目组成,测验项目质量的好坏直接决定了测验的质量。精确掌握每个测验项目区分度参数和难度参数的相关信息,对于教育和心理测验项目的筛选以及测验的编制具有重要的参考价值(涂冬波,蔡艳,戴海琦,丁树良,2011)。另外,计算机化自适应测验(

    Computerized Adaptive Testing

    ,CAT)自20世纪70年代早期被引入测验领域,而实施 CAT需要一个优质、大型的题库,同时题库还需要不断更新(陈平,辛涛,2011),淘汰一些质量不够好的试题,加入一些新的试题。可见,对项目参数进行准确估计就非常重要(Maij-de Meij,Kelderman,&van der Flier,2008)。

    目前,国内外对项目参数估计精度的研究,大部分是基于在已知项目参数真值的情况下,运用各种参数估计方法(常用的参数估计方法有极大似然法、贝叶斯方法、MCMC方法等)产生新的估计值,再和真值进行偏度(BIAS)和均方根差(RMSE)的比较,从而说明该种估计方法的有效性(Liang &Wells,2009;Finch,2010) 。均方根差RMSE、Bias的计算公式分别为：

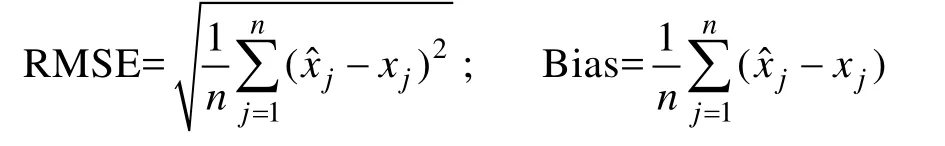
    其中

    x

    表示第

    j

    个项目参数(a或 b)的真值,x

    表示第

    j

    个项目参数的估计值,n

    表示重复试验的次数。通过公式可看出,均方根差反映的是

    n

    次重复试验中项目参数真值与项目参数估计值之间的平均偏差大小;偏差的值反映了项目参数真值与参数估计值之间偏差的平均。这种方法只能得出每个参数真值的估计误差,无法反映不同的参数之间的估计误差是如何随着参数真值的变化而变化的。

    为了弥补这些缺陷,本文尝试从项目参数信息函数的角度出发,研究二参数逻辑斯蒂模型项目参数的估计精度。目前,国内外主要研究能力参数的信息函数,而对于项目参数的信息函数还没有人研究,本文尝试填补这一空缺。同时还探索了影响估计精度的主要因素有哪些,以及这些因素是怎样影响项目参数的估计精度的。希望通过本文的研究,能够为题库编制者和测验编制者提供一些有价值的参考信息 ......