简小珠 戴步云 戴海琦

    (1井冈山大学教育学院, 江西 吉安 343009)

    (2江西师范大学心理学院, 江西省心理与认知科学重点实验室, 南昌 330022)

    1 前言

    1.1 以往的多级记分模型

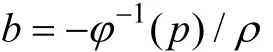
    1.2 多级记分试题的试题属性

    多级记分试题的试题属性主要表现为：(1)用试题满分值来表达试题知识考查重要性程度的加权作用; (2)用平均得分比例来表达被试群体在多级记分试题上的平均难度。

    第一个属性：试题考查重要性程度加权作用。从测验设计来看, 多级记分试题的赋分基本思想：给予某一道试题赋予更大的分数权重, 是为了增大该试题在整份测验中的分数权重比例, 以反映所考查知识与能力的重要性。正如教学内容、测验内容具有难点与重点, 试题也具有难易程度与考查重要性这两个属性。因此, 反映在IRT模型上应使用不同的参数来表达多级记分试题的难度、重要性。试题难易程度是通过难度来体现, 而试题所测量内容的重要性则需通过分数权重, 即权重参数来表达。试题所测量内容重要性可通过该试题满分值、或该试题所在内容模块总分在整份测验总分的比重来体现。本文提出的Logistic加权模型将包含权重参数。

    第二个属性：试题的平均难度。被试群体在多级记分试题上的得分为：得1分及以上的人数比例最大, 得2分及以上的人数比例依次减小, 依此类推, 得满分的被试人数比例最小。多级记分题的评分点结构、评分等级相对复杂, 为简化认识, 可使用平均难度表达被试群体在多级记分试题上的得分比例, 也就是说, 计算被试群体在多级记分试题上的平均得分, 并除以该试题满分值得到平均得分比例

    P

    , 即平均难度。1.3 GRM在多级记分试题上应用的不足

    GRM在多级记分试题上应用的不足：第一,GRM下多级记分试题的项目信息量并不是两级记分试题的倍数。分别计算一道满分为5分, 区分度为1, 难度参数分别为?1, ?0.5, 0.0, 0.5, 1的多级记分试题, 和一道区分度为1, 难度为0.0的两级记分试题的项目信息量, 发现该多级记分试题的项目信息量在能力量尺的各个点上都仅仅比两级记分试题多0.1～0.2。第二, GRM有时无法适合实际情境,(1)如果最后一个等级得分的被试太少, 会严重影响难度参数的估计(Embretson & Reise, 2000) ......