直观奇妙的“形数”(1)
所谓“形数”,顾名思义就是指有形状可以构成图形的数。相信许多读者一定会感到奇怪:数怎么会有形状呢?这得从其发明者—古希腊最著名的数学家毕达哥拉斯说起。
毕达哥拉斯研究数的概念时,喜欢把数描绘成沙滩上的小石子,而小石子又能够摆成不同的几何图形,于是,就产生一系列的“形数”。譬如,当小石子的数目是1、3、6、10等数字时,小石子都能被摆成正三角形,这些数就叫“三角形数”;当小石子的数目是1、4、9、16等数字时,它们都能够被摆成正方形,这些数就叫“正方形数”(如图1)。
▲ 图1
除此之外,毕达哥拉斯还摆出了多边形数,并进一步发现了各种“形数”之间的内在联系。由此,“形数”正式面世并引发了世人的关注。
, 百拇医药 羊群、石子和形数
有一天,毕达哥拉斯到郊外的一个牧场散步,遇到一位须发皆白的老翁正在那里牧羊。见了绿油油的草地,羊群四散开来,它们争先恐后地啃食鲜嫩的青草。正在一旁玩石子的牧羊老翁认出身边的人就是大名鼎鼎的数学家毕达哥拉斯,便与他闲聊起来。
其间,毕达哥拉斯随口问道:“老先生,您放的这群羊一共有多少只?”
老翁望了望远处的羊群,忽然眼前一亮,说道:“真是巧了!我的这群羊,除去待在我身边的这只头羊,其他的刚好是按1、3、5、7……分成若干群。最多的一群,我刚刚数了数,共有17只。至于总共有多少只嘛,大师,您能数出来吗?”
见牧羊老翁并未直接回答,反而出了道难题,要考考自己,毕达哥拉斯也不多说,蹲下身,捡拾地上的石子。
“您是全希腊绝顶聪明的大师,请原谅我没有直接回答您的问题。我就是想见识见识您的非凡智慧。”牧羊老翁解释道。
, 百拇医药
“总共应该有82只吧。”毕达哥拉斯头也不抬地答道。
听了这话,牧羊老翁愣住了:沒想到,毕达哥拉斯这么快就算出来了!他不禁脱口而出:“这也太神奇了!”
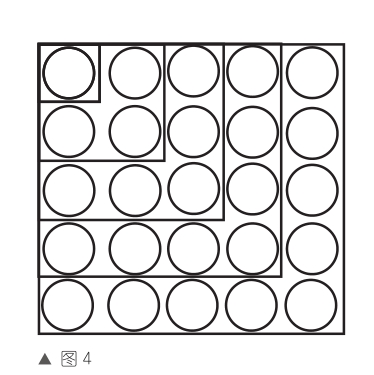
牧羊老翁向毕达哥拉斯请教其中的玄机。毕达哥拉斯不慌不忙地摆弄起地上的石子,又用老翁牧羊用的鞭子在摆好的石子旁画上方框(如图2);然后,指着地上的图形,解释道:“您瞧,第一个方格里放了1块石子,可以看作1=1×1;第二个方格里放的石子数是1块和3块,刚好有1+3=2×2;第三个方格里放的石子数是1块、3块和5块,刚好有1+3+5=3×3;第四个方格里的石子数就是1+3+5+7=4×4;第五个方格里的石子数就是1+3+5+7+9=5×5……这就是用图形直观表示的‘形数’。”
老翁恍然大悟,兴奋地答道:“按照这样的规律依次类推,1、3、5、7、……、17只羊共有9群,那么1+3+5+…+15+17=9×9=81,再加上我身边的这只头羊,总共就有82只羊。对吧?”
, 百拇医药
毕达哥拉斯点头称是。
“怪不得今天的羊群分布得如此奇特,原来就是为您的‘形数’准备的啊!”牧羊老翁连连感叹自己大开眼界,称赞毕达哥拉斯名不虚传。
三角形数和正方形数
毕达哥拉斯把自然数看成是点的集合,尤其对可以排成三角形、正方形的数情有独钟,因此,研究两者之间的某些奇妙关联就在情理之中。
众所周知,自然数的构成是1、2、3、4、5、6、7、8、9、10、……“三角形数”实际上就是从1开始的一些连续自然数的和(参照图1):
1、3、6、10、15、21、28、36、45、55、66、……、1225……①
, 百拇医药
“正方形数”实际上就是自然数a的平方a2:
1、4、9、16、25、36、49、64、81、100、……、1225……②
1、36、1225、41616、1413721、48024900……③
耐人寻味的是,如果对数列③继续探究,便会发现,这类既是三角形数又是正方形数的数,是两个正方形数的积的平方,可写成一般式b2c2。譬如,
瞧,上面提到的b、c神奇地在分子、分母中悄然出现,让人不得不瞠目惊叹!
形数和数学公式
毕达哥拉斯利用“形数”发现了许多自然数的规律和定理,并直观归纳出一些重要而常用的数学公式。下面撷取数则,以飨读者。
三、求连续偶数的和的公式:2+4+6+…+2n=n(n+1), http://www.100md.com(林革)
毕达哥拉斯研究数的概念时,喜欢把数描绘成沙滩上的小石子,而小石子又能够摆成不同的几何图形,于是,就产生一系列的“形数”。譬如,当小石子的数目是1、3、6、10等数字时,小石子都能被摆成正三角形,这些数就叫“三角形数”;当小石子的数目是1、4、9、16等数字时,它们都能够被摆成正方形,这些数就叫“正方形数”(如图1)。

▲ 图1
除此之外,毕达哥拉斯还摆出了多边形数,并进一步发现了各种“形数”之间的内在联系。由此,“形数”正式面世并引发了世人的关注。
, 百拇医药 羊群、石子和形数
有一天,毕达哥拉斯到郊外的一个牧场散步,遇到一位须发皆白的老翁正在那里牧羊。见了绿油油的草地,羊群四散开来,它们争先恐后地啃食鲜嫩的青草。正在一旁玩石子的牧羊老翁认出身边的人就是大名鼎鼎的数学家毕达哥拉斯,便与他闲聊起来。
其间,毕达哥拉斯随口问道:“老先生,您放的这群羊一共有多少只?”
老翁望了望远处的羊群,忽然眼前一亮,说道:“真是巧了!我的这群羊,除去待在我身边的这只头羊,其他的刚好是按1、3、5、7……分成若干群。最多的一群,我刚刚数了数,共有17只。至于总共有多少只嘛,大师,您能数出来吗?”
见牧羊老翁并未直接回答,反而出了道难题,要考考自己,毕达哥拉斯也不多说,蹲下身,捡拾地上的石子。
“您是全希腊绝顶聪明的大师,请原谅我没有直接回答您的问题。我就是想见识见识您的非凡智慧。”牧羊老翁解释道。
, 百拇医药
“总共应该有82只吧。”毕达哥拉斯头也不抬地答道。
听了这话,牧羊老翁愣住了:沒想到,毕达哥拉斯这么快就算出来了!他不禁脱口而出:“这也太神奇了!”
牧羊老翁向毕达哥拉斯请教其中的玄机。毕达哥拉斯不慌不忙地摆弄起地上的石子,又用老翁牧羊用的鞭子在摆好的石子旁画上方框(如图2);然后,指着地上的图形,解释道:“您瞧,第一个方格里放了1块石子,可以看作1=1×1;第二个方格里放的石子数是1块和3块,刚好有1+3=2×2;第三个方格里放的石子数是1块、3块和5块,刚好有1+3+5=3×3;第四个方格里的石子数就是1+3+5+7=4×4;第五个方格里的石子数就是1+3+5+7+9=5×5……这就是用图形直观表示的‘形数’。”
老翁恍然大悟,兴奋地答道:“按照这样的规律依次类推,1、3、5、7、……、17只羊共有9群,那么1+3+5+…+15+17=9×9=81,再加上我身边的这只头羊,总共就有82只羊。对吧?”
, 百拇医药
毕达哥拉斯点头称是。
“怪不得今天的羊群分布得如此奇特,原来就是为您的‘形数’准备的啊!”牧羊老翁连连感叹自己大开眼界,称赞毕达哥拉斯名不虚传。

三角形数和正方形数
毕达哥拉斯把自然数看成是点的集合,尤其对可以排成三角形、正方形的数情有独钟,因此,研究两者之间的某些奇妙关联就在情理之中。
众所周知,自然数的构成是1、2、3、4、5、6、7、8、9、10、……“三角形数”实际上就是从1开始的一些连续自然数的和(参照图1):
1、3、6、10、15、21、28、36、45、55、66、……、1225……①
, 百拇医药
“正方形数”实际上就是自然数a的平方a2:
1、4、9、16、25、36、49、64、81、100、……、1225……②

1、36、1225、41616、1413721、48024900……③
耐人寻味的是,如果对数列③继续探究,便会发现,这类既是三角形数又是正方形数的数,是两个正方形数的积的平方,可写成一般式b2c2。譬如,

瞧,上面提到的b、c神奇地在分子、分母中悄然出现,让人不得不瞠目惊叹!
形数和数学公式
毕达哥拉斯利用“形数”发现了许多自然数的规律和定理,并直观归纳出一些重要而常用的数学公式。下面撷取数则,以飨读者。


三、求连续偶数的和的公式:2+4+6+…+2n=n(n+1), http://www.100md.com(林革)