内隐学习的人工神经网络模型(1)
 |
 |
 |
摘 要 近年来,人工神经网络模型常被用来模拟各种心理活动,从而为心理学的一些相关理论提供丰富的证据,内隐学习也不例外。基于权重调整来学习正确反应的人工神经网络模型和内隐学习的两大本质特征间有着极为相应的匹配,因此,人工神经网络模型特别适用于内隐学习研究。到目前为止,针对两种较为普遍的内隐学习任务,已经相应地出现了两种使用较为广泛的神经网络模型——自动联系者和简单循环网络。
关键词 人工神经网络模型,人工语法学习,自动联系者,序列学习,简单循环网络。
分类号 B842
1 引言
人工神经网络模型(Artificial Neural Network Model,简称ANN),顾名思义,就是用人造的程序、机械或设备来模拟人脑神经网络的模型。人工神经网络模型的用途有二:(1)发明基于神经网络的人工智能系统,来模拟人的学习、记忆、推理等智能活动,以服务于人类的现实生活;(2)构建各种心理活动和心理过程的模型,以为各种心理学理论提供支持。前者是自动化、通信、制造、经济领域关注的,我们平时所见的语音识别、经济领域使用的股票走势预测等智能系统大多是基于人工神经网络模型研制出来的。而后者则是心理学家所关注的领域。至今,人工神经网络模型已被用来模拟诸如知觉、记忆、学习、判断等各种心理活动,以解释矛盾的实验数据,为有关的心理学理论提供丰富的证据。
, 百拇医药
和其他领域的研究者们一样,内隐学习领域的研究者们也注意到了这一行之有效的工具。Cleeremans(1993)指出根据已有的内隐学习理论构造人工神经网络模型,将模型的输出数据与人类被试的实验数据进行比较,能为原有的理论观点提供证据[1]。Dienes和Perner(1996)也有类似的看法[2]。然而,在发挥人工神经网络模型在内隐学习研究上的功效之前,必须解决如下问题:人工神经网络模型是否正如Cleeremans等所言适用于内隐学习研究?如果是,用哪类人工神经网络模型来模拟内隐学习?
2 人工神经网络模型的工作原理及其研究内隐学习的适用性
人工神经网络模型之所以适用于内隐学习,是因为它的基本工作原理和内隐学习的两个本质特征有着惊人的相似。
2.1 人工神经网络模型的工作原理
早在20世纪40年代,便有研究者对人工神经网络模型的工作原理做了最初的尝试。1943年,McCulloch和Pitts用类似“开关”的阈限逻辑单元(Threshold Logic Unit)**来模拟神经元,并将多个这样的单元以相等的强度(权重)连接起来,形成网络,这就是著名的MP模型[3]。1949年,Hebb在论述条件反射的形成时,无意间提到了神经元间连接强度更新的重要法则,即两个彼此相连的神经元同时激活或同时抑制,都能增加神经元间的连接强度,后人称此为Hebb法则[4]。然而,MP模型和Hebb法则都不能构成真正意义**上的神经网络模型,虽然,MP模型已经具备将多个神经元连接起来,形成网络的雏形,但是由于不同单元间的连接强度相等,且恒定不可变化,MP模型不具备人工神经网络的基本特征——学习性;而Hebb虽然提出了权重变化的一条有效法则,但却未将其应用到人工神经网络中来。真正将神经元连接成网络的思想与借助于权重更新使网络具有学习性的思想综合在一起的要属Rosenblatt。
, 百拇医药
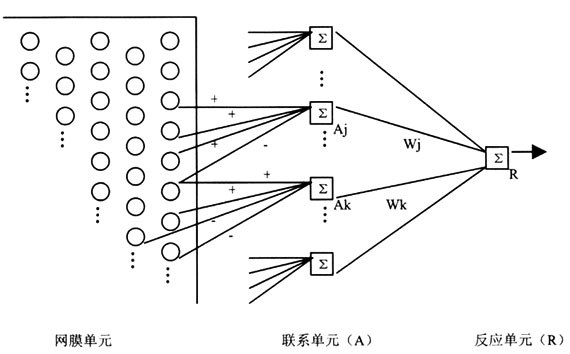
Rosenblatt(1958)提出了第一个真正意义上的人工神经网络模型——感知器(Perceptron)[5]。其基本工作原理为:整个感知器由多个不同层次的加工单元组成,每个加工单元的功能类似于单个神经元或一组神经元,它能接收来自前一层的几个加工单元的激活,并综合这些激活,对此进行简单运算(例如:判断总激活量是否达到某一阈限),然后将运算的结果传递给下一层的加工单元。第一层单元的激活模式反映了外部刺激状态,即模型的输入,而最后一层单元的激活模式则为模型的输出反应。某个单元对下一层的另一个单元的影响取决于两个单元之间连接的强度(权重)。为了在给定输入的情况下,使模型获得类似于人类被试的输出反应,必须不停地调节单元与单元间的连接权重。所以,在构建合适的人工神经网络模型时,研究者往往会先设置一系列初始权重,然后不断地给予模型不同的输入模式,在每个特定输入后,比较模型输出与正确输出间的差异,并据此调整单元间的连接权重,这一过程不断进行,直到模型输出和正确输出间的差异达到最小值,此时,模型便完成了整个学习过程。图1为一个典型感知器的例子,它旨在判断呈现于视网膜的光条是垂直的还是水平的。整个感知器由3个加工单元层组成,第一层为网膜层,即将整个视网膜分割为10×10的网格,用每个网膜单元对应于一个网格,共100个单元,当光条落
, 百拇医药
图1 感知器例子(资料来源:文献[3])
在视网膜的某几个网格上时,这些网格所对应的网膜单元被激活。第二层为联系层,其中的每个单元总是和某些网膜单元间存在兴奋或抑制连接,不论兴奋还是抑制连接,强度都是恒定的1或-1,当与联系单元连接的网膜单元的总激活量达到联系单元的激活阈限时,联系单元被激活,例如图1,Aj的接收到的总激活量为1+1+1-1=2,如果Aj的阈限为2,那么2=2,Aj被激活。第三层为反应层,其中只包括一个反应单元,它与所有的联系单元连接,连接权重为Wj,其中,j表示第j个联系单元。反应单元将综合来自联系单元的激活信息,即将每个联系单元的激活量乘以它们之间的连接权重,然后简单求和,得出总激活量,并判断激活是否达到阈限,公式表示如下:
aR为反应单元的激活水平,aj为联系单元的激活水平,θ为阈限值。如果,总激活量达到反应单元的阈限,反应单元被激活(激活量为1),感知器决定光条为垂直,否则,反应单元不被激活(激活量为0),感知器反应光条为水平。当然,感知器必须经过一个漫长的学习阶段,才能完成这一简单的判断任务。在学习阶段,感知器接受各种不同的水平和垂直光条刺激,并一一做出反应,当反应正确时,连接权重不做任何调整,一旦反应错误,感知器会自动调整联系单元与反应单元间的权重,比如:当反应单元的激活量为0时,而实际光条为垂直,说明反应单元所接收到的总激活量小于阈限,此时,则应增大那些被激活的联系单元与反应单元间的连接权重,以提高总激活量,使其更有可能达到阈限,致使在下次刺激呈现时,感知器更易做出正确反应。当然,Rosenblatt的感知器除了能调整权重外,还会调整反应单元阈限。这种通过逐步调整连接权重和阈限,以减少感知器反应和正确反应间的差距的方法就是著名的感知器收敛法则(perceptron convergence rule)。不过,调整阈限的方法对于拥有多个反应单元的模型来说过于复杂,所以未被以后的人工神经网络模型采纳。
, 百拇医药
可见,Rosenblatt的贡献是卓越的,他给出了人工神经网络的基本工作原理,基于感知器收敛法则发展而来的delta法则与斜率递减(gradient descent)法已成为如今人工神经网络最主要的算法,本文第3点中将对此做详细介绍。然而,值得注意的一点是感知器仅在联系层和反应层间使用了权重概念,学习过程也仅发生在这两层之间,所以从本质上讲,感知器只属于包含一个输入层和一个输出层的单层网络(single layer network),这种单层网络在解决某些实际问题时,遇到了障碍。Minsky等(1969)指出感知器甚至无法模拟诸如XOR(异或)等简单运算[3]。因此,在接下来的将近20年中,人工神经网络的发展一度进入低迷期。直到80年代中期,逆向传导法(back propagation)[6]、自动联系者(atuoassociator)[7]、循环模型(recurrent model)[8,9]一一提出,多层网络广泛应用智能模拟任务中,人工神经网络才得以迅速发展。然而,这些算法和模型的基本工作原理与最初的感知器却并无两样。
[ 下 页 ], http://www.100md.com(郭秀艳 朱 磊 魏知超)