陈宇帅 温忠麟 顾红磊

    (华南师范大学心理应用研究中心/心理学院, 广州 510631)

    在心理学研究中, 由于许多人格特质、内隐态度等的不可直接观测性, 潜变量模型得到广泛应用, 其中因子分析(Factor Analysis, FA)比较流行。然而, FA的样本同质性假设在许多场合可能不成立(Jedidi, Jagpal, & DeSarbo, 1997; Yuan &Bentler, 2010)。许多研究样本中包含不同性别、年级, 或者不同能力、态度的个体, 异质性可能是普遍存在的。假定所有个体具有相同的参数值往往与实际相悖, 产生模型拟合不佳等结果。尽管多组模型(multiple-group models)能够处理外显异质性, 但对于样本潜在的异质性则显得无能为力。为了解决这一问题, 因子混合模型(Factor Mixture Model, FMM)作为一种新的分析技术应运而生。

    FMM是潜在类别分析(Latent Class Analysis,LCA)与FA的结合, 继承了两种分析技术的优点,弥补了各自的局限, 为研究者提供了一个全新的视角, 但目前实际应用还不多。本文以FMM为主题, 首先介绍了FMM的基本形式, 包括数学模型及基本原理; 接着归纳了FMM的主要优势以及实际应用, 然后总结了FMM的分析步骤, 并以一个实例进行示范; 最后就FMM有待完善的问题,提出研究展望。

    1 FA、LCA与FMM简介

    1.1 FA简介

    FA作为多元统计中重要的方法之一为研究者广泛使用, 其目的在于通过一个或多个因子来解释各指标间的关联, 从而实现对指标的分组。本文考虑的FA模型仅限CFA模型。以图1中的M1为例, 假定模型中有r个指标, 测量了两个因子η1和η2, 其中前t个指标测量了η1, 其余指标测量了η2。模型可用如下方程表示：

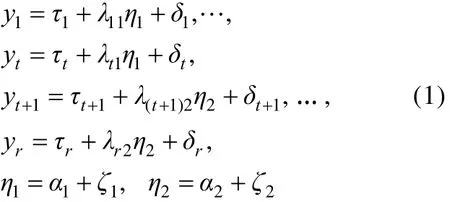
    在上述方程中,y1表示第1个指标,τ1表示y1的截距,λ11表示y1在η1上的负荷,δ1表示y1的误差,α1表示因子η1的均值,ζ1表示η1的离均差(残差),其余符号类推。

    1.2 LCA简介

    LCA是一种通过类别潜变量来解释指标间的关联, 进而实现指标间局部独立的统计方法。与FA相比, 两者在形式上颇为相似(见图1中的M1和M2), 但两者存在本质差异 ......