初中教师教学有效性评价问卷的编制:以学生为评价主体的视角(2)
 |
 |
 |
 |
 |
 |
200名1-3年级的初中生,50名各科教师。
分别分析两个样本对项目重要性的评价,删除两个样本中共同认为不重要的项目。首先计算各项目得分的平均数和标准差,接着剔除平均数低、标准差大的项目。平均分高表明项目的重要性高,标准差小表明评定者对项目的重要性程度评定结果一致,重要性分析最终删除5个的项目,并修改了另外8个项目,这样就形成了本研究的初测问卷,共计47个项目。
4 问卷初测和项目分析
被试为山东某中学的1-3年级的415名初中生。
4.1 初测问卷的项目区分度分析
首先计算出每个维度的总分,再计算出每个项目与所在维度总分之间的相关,删除区分度较小的项目。初测问卷中的项目区分度都在0.5以上,所以在这里没有删除项目,
, 百拇医药
4.2 初测问卷的因素分析
验证性因素分析不仅可以对已有假设的测量结构进行验证,而且可以根据因素分析中提供的信息,如因素载荷、修正指数等,对项目的测量信度、项目与假设因素之间的关系以及项目与项目之间的关系进行分析,进而淘汰不好的项目。验证性因素分析所用软件为LISREL8.53。剔除项目的规则如下:
(1)剔除因素载荷在指定因素上小于0.40的项目:
(2)根据修正指数的结果,剔除掉允许项目与其他因素上的载荷自由估计时,修正指数较大的项目:
(3)根据修正指数,剔除掉允许项目特殊因子相关时,修正指数较大的项且,通过验证性因素分析共删掉14个项目,保留33个项目,最后形成33个项目的正式问卷。5正式问卷的结构与测量指标分析
这一步的主要目的是对正式问卷的结构和心理测量学指标进行分析。被试来自山东的三所中学,共计1159名初中生。
, 百拇医药
5.1 项目区分度分析
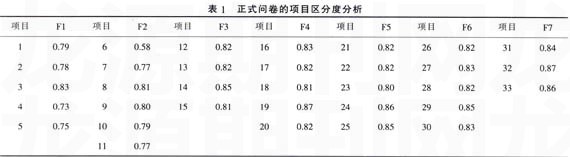
分别求测验中每个项目与所在维度平均分数的相关,结果如表1,
从表1可以看出,项目与所在维度平均分的相关都在0.50以上,说明问卷中的项目具有较好的区分度。
5.2 一致性信度分析
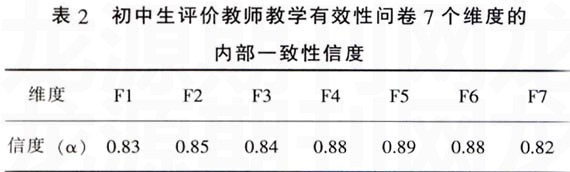
采用克隆巴赫(Crombach a)一致性系数来检验各个维度的信度指数,结果如表2。
表2的结果表明,7个维度的α系数都在0.82以上,整个问卷的一致性信度(α系数)为0.968,说明整个问卷具有较高的信度指标。
5.3 结构效度分析
根据理论假设和前面的分析,整个问卷有7个维度,提出本问卷的一阶7因素模型。
, http://www.100md.com
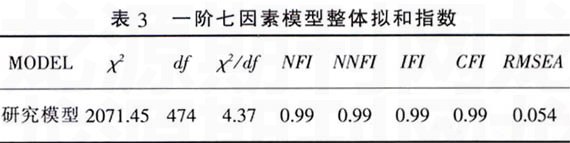
用LISREL8,53对一阶7因素模型进行验证性因素分析,得到模型的整体拟和情况如表3。
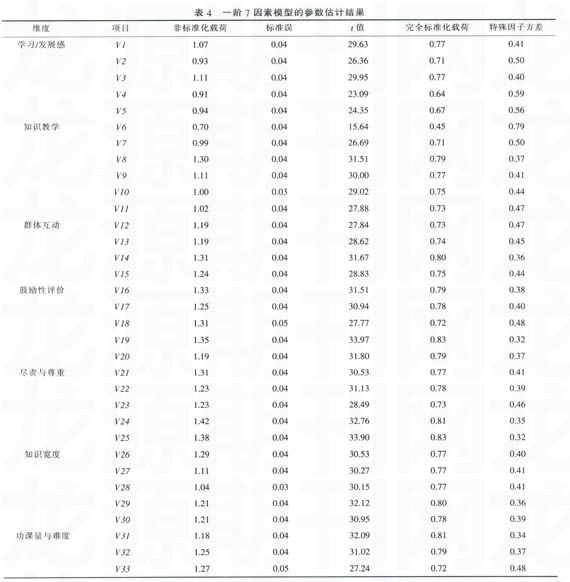
根据Chou,Bentler和Pentz(1998)及Bvrne(1998)提出的优良模型的判定标准,NFI、NNFI、IFI和CFI的值一般应大于0.900,RMSEA的值小于0.080。对于一阶七因素的假设模型,从模型拟合指数可以看出:各项指标均在一个优良的拟合模型可以接受的范围(虽然)2/df的值较大,因,X2/df受样本容量影响,在大样本时,仅供参考),因此,从整体上数据与定义模型拟合较好,接受一阶7因素模型的假设,表4是一阶7因素模型的参数估计结果,
从因素载荷的估计结果可以看出。所有非标准化因素载荷都达到显著的水平,完全标准化载荷都在0.40以上,特殊因子的方差也比较小,说明问卷中的项目有较好的信度。
5.4 交叉效度分析
, http://www.100md.com
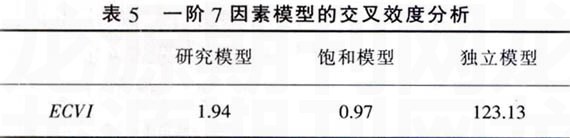
交叉效度分析是指对在一个样本数据中所探索出的模型再用另外一个样本进行验证。Cudeck与Browne建议采用交叉效度拟合指数来检验模型的交叉效度,以推论在其他样本和总体中的合理性。交叉效度拟和指数(CVI)是一个随机变量,因两次使用随机样本,随机误差较为复杂。为此,Browne与Cudeck利用单个样本导出了CVI的数学期望的估计即ECVI㈣。在嵌套模型序列中,饱和模型约束最少,拟和最好,所以ECVI的值最小。独立模型约束最多,拟和最差,所以ECVI的值最大。因此,在一般情况下,介于二者之间的模型的ECVI值愈接近饱和模型的ECVI值,拟和愈好;愈接近独立模型的ECVI值,表示拟和愈差。本研究中的一阶7因素模型的ECVI的值以及饱和模
从表5可以看出,在本研究中所定义的研究模型的ECVI的值为1.94,相比饱和模型ECVI的值(0.97)和独立模型的ECVI的值(123.13),更接近于饱和模型的ECVI的值(0.97),说明所定义的一阶7因素模型具有较好的交叉效度。
, 百拇医药
5.5 不同特征群体测量结构稳定性分析
这一步的目的是检验对于不同特征的样本群体,如不同的性别、年龄等样本而言,测量工具的恒等性。本研究采用Byme和Shavelson(1987)及Marsh和Hocevar(1985)的方法旧。首先检验不同组是否具有相同的因素结构;然后在此基础上再检验项目与因素之间是否具有相同的载荷:最后考察不同组检验因素之间的协方差矩阵是否相等。为了检验上述问题,可以通过定义下面的嵌套模型:
模型1(基准模型):验证不同样本组是否具有相同的模型结构:即一阶7因素模型,对其他条件部分不加任何限制:
模型2(限定因素载荷相等):在模型1的基础上限定不同组测量部分所有因素载荷相等:
模型3:在模型2成立的基础上,对于不同组,限定潜变量方差、协方差相等。
, http://www.100md.com
由于上面所定义的模型之间具有嵌套结构,因此根据Byme和Shavelson的方法,可以通过两个嵌套模型卡方值差异的显著性来检验模型中的限定条件是否成立,表6和表7是分别考虑不同性别、年级时假设模型测量结构稳定性的分析结果,2:2871,65-2814,16=57.49。自由度的差异aDF=974-948=26。对于自由度为26的卡方分布,在0.01的显著性水平下,卡方值57.49达到显著差异。不同性别组因素载荷差异最大的项目是第9题,二者之间的差也仅为0.06,模型2与模型1卡方值差异显著很可能是由于样本量较大所引起的(男生组为614,女生组为545)。对于样本量较大的情况,也可以采用Pohl等介绍的方法计算卡方检验的效应量,0.3为中等效应量,模型1与模型2比较计算得到的效应量小于0.3,所以模型2中,不同性别组因素载荷相等的假设成立,也就是说对于不同的性别组,测验中的项目具有相同的信度。在模型2的基础上,进一步限定因素的协方差相等,结果模型3与模型2拟合卡方值的差异为△x2=2957.17-2871,65=85.52,两个模型自由度之差为28,对于自由度为28的卡方分布,达到显著差异,根据, http://www.100md.com